Производная функции в точке
Рассмотрим функцию 
(синий график), которая определена и непрерывна на некотором интервале, произвольную точку 
, принадлежащую данному интервалу, и соответствующее значение 
:
Зададим аргументу функции приращение 
(красный отрезок) в точке .
Приращение аргумента повлекло за собой приращение функции:
(малиновый отрезок)
В данном случае 
, поскольку в качестве примера выбран промежуток, на котором функция возрастает.
Угол наклона секущей к оси 
я обозначил через 
и отметил его коричневой дугой в двух местах. Такое внимание к данному углу не случайно – он однозначно определяется приращениями 
. Рассмотрим прямоугольный треугольник 
и угол 
. Согласно школьному определению, тангенс угла равен отношению противолежащего катета к прилежащему катету: 
Определение: производной функции в точке 
называется предел отношения приращения функции 
к вызвавшему его приращению аргумента 
в этой точке при 
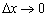. Или коротко:
Если данный предел конечен, то функция является дифференцируемой в точке . А то, что в львиной доле случаев предел 
существует и конечен, скептики убедятся в самом ближайшем будущем.
И, конечно же, не забываем о важнейшей особенности предела, как такового: ПРИНЦИПИАЛЬНЫЙ МОМЕНТ состоит в том, что приращение аргумента стремится к нулю, но нуля не достигает, иными словами, величина бесконечно малА, но не равна нулю!
Геометрический смысл производной
Пожалуйста, возьмите в руки обычную линейку и совместите её ребро с прямой 
.
Теперь, согласно определению производной 
, медленно двигаем линейку влево к точке , уменьшая тем самым приращение . При этом приращение функции 
тоже уменьшается.
В результате секущая
стремится занять положение касательной 
к графику функции в точке . Искомая касательная изображена зелёным цветом.
Таким образом, мы получили строгое определение касательной к графику функции:
Касательная к графику функции в точке – это предельное положение секущей в данной точке.
Вспомним полученную ранее формулу тангенса угла наклона секущей 
и осуществим в обеих её частях так называемый предельный переход.
В свете рассматриваемых событий (бесконечного уменьшения и нахождения предела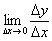 
) угол наклона секущей стремится к углу наклона
касательной (последний дважды отмечен зелёными дугами). Аналогичное утверждение справедливо и для тангенсов данных углов: 
. В итоге:
Вывод: производная функции в точке численно равна тангенсу угла наклона касательной к графику функции в данной точке: 
.
А тангенс угла наклона касательной – это в точности её угловой коэффициент:
В курсе аналитической геометрии выведена формула, по которой можно составить уравнение прямой с угловым коэффициентом:
Учитывая полученное равенство 
, перепишем уравнение в виде 
.
Данной формулой мы уже активно пользовались, когда находили уравнение касательной, и сейчас стало ясно, откуда она взялась.
Существование производной в точке и непрерывность функции
По определению: 
, следовательно, существование производной в точке тесно связано с существованием предела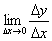 
в данной точке.
В определении производной ВАЖНЕЙШИМ является тот факт, что приращение аргумента задаётся и в другую сторону.
Отложите на чертеже небольшой отрезок слева от точки 
. При этом точка 
расположится левее точки , а точка 
– ниже точки 
. Теперь проведите секущую графика функции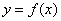 
и начните мысленно уменьшать приращение вправо к точке . В результате данная секущая будет стремиться занять положение той же самой «зелёной» касательной!
Примечание: приращение с левой стороны осуществляется «против оси абсцисс» и поэтому отрицательно: 
. Заметьте, что всё остаётся корректным, так, в нашем случае соответвующее приращение 
тоже меньше нуля, и по этой причине левосторонний предел таки будет положительным 
, корректно показывая (как и его правосторонний коллега) рост функции в точке . Односторонние пределы конечны и совпадают, что говорит о существовании общего предела, производной и единой касательной.
Таким образом, существование производной в точке геометрически очень удобно ассоциировать с существованием ОБЩЕЙ КАСАТЕЛЬНОЙ в данной точке.
Очевидно, что функция не дифференцируема в точках разрыва. Во-первых, она может быть не определена в такой точке, следовательно, приращение задать невозможно (на нет и суда нет). А во-вторых, практически всегда попросту не существует общего предела
Вывод: из дифференцируемости функции в точке необходимо (обязательно) следует её непрерывность в данной точке.
Однако обратное утверждение в общем случае неверно, то есть из непрерывности функции дифференцируемость следует далеко не всегда! Классический пример, функция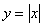 
в точке 
Если рассмотреть приращение справа, то правосторонний предел будет равен 
, и, соответственно, получаем касательную 
, совпадающую с правой частью графика 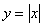. Если же придать приращение аргументу влево, получается совсем другой результат: 
и другая касательная 
, которая совпадает с левой частью графика 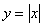. Ни общего предела, ни общей касательной. Таким образом, функция 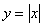хоть и непрерывна в точке , но не дифференцируема в ней!
Особый случай.
Когда предел равен «плюс» или «минус бесконечности», то производная тоже может существовать и касательная к графику функции будет параллельная оси 
. Например, касательной к графику функции 
в точке является сама ось ординат.