До сих пор речь шла о производной и дифференциале в единственной «подопытной» точке  . Но ведь в качестве
. Но ведь в качестве  можно взять ЛЮБУЮ ТОЧКУ
можно взять ЛЮБУЮ ТОЧКУ  рассматриваемого интервала!
рассматриваемого интервала!
Из этих соображений в равенстве  проведём замену
проведём замену  и получим
и получим 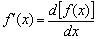 . А это не что иное, как обозначение производной
. А это не что иное, как обозначение производной  , Символ
, Символ  используется двояко – и как цельный символ производной, и как частное дифференциалов. Вторая интерпретация активно эксплуатируется в ходе решения дифференциальных уравнений.
используется двояко – и как цельный символ производной, и как частное дифференциалов. Вторая интерпретация активно эксплуатируется в ходе решения дифференциальных уравнений.
Естественно, и в самом определении производной в точке  заменим
заменим  на
на  :
:
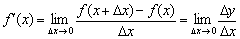
К чему мы пришли? А пришли мы к тому, что для функции  по закону
по закону  ставится в соответствие другая функция
ставится в соответствие другая функция  , которая называется производной функцией (или просто производной).
, которая называется производной функцией (или просто производной).
Производная  характеризует скорость изменения функции
характеризует скорость изменения функции  . Рассмотрим некоторую точку
. Рассмотрим некоторую точку  области определения функции
области определения функции  . Пусть функция дифференцируема в данной точке. Тогда:
. Пусть функция дифференцируема в данной точке. Тогда:
1) Если 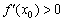 , то функция
, то функция  возрастает в точке
возрастает в точке  . И, очевидно, существует интервал (пусть даже очень малый), содержащий точку
. И, очевидно, существует интервал (пусть даже очень малый), содержащий точку  , на котором функция
, на котором функция  растёт, и её график идёт «снизу вверх».
растёт, и её график идёт «снизу вверх».
2) Если  , то функция
, то функция  убывает в точке
убывает в точке  . И существует интервал, содержащий точку
. И существует интервал, содержащий точку  , на котором функция
, на котором функция  убывает (график идёт «сверху вниз»).
убывает (график идёт «сверху вниз»).
3) Если  , то бесконечно близко около точки
, то бесконечно близко около точки  функция
функция  сохраняет свою скорость постоянной. Так бывает, как отмечалось, у функции-константы и в критических точках функции, в частности в точках минимума и максимума.
сохраняет свою скорость постоянной. Так бывает, как отмечалось, у функции-константы и в критических точках функции, в частности в точках минимума и максимума.
Немного семантики. Что в широком смысле обозначает глагол «дифференцировать»? Дифференцировать – это значит выделить какой-либо признак. Дифференцируя функцию  , мы «выделяем» скорость её изменения в виде производной функции
, мы «выделяем» скорость её изменения в виде производной функции  . А что, кстати, понимается под словом «производная»? Функция
. А что, кстати, понимается под словом «производная»? Функция  произошла от функции
произошла от функции  .
.
Термины весьма удачно истолковывает механический смысл производной:
Рассмотрим закон изменения координаты тела  , зависящий от времени
, зависящий от времени  , и функцию скорости движения данного тела
, и функцию скорости движения данного тела  . Функция
. Функция  характеризует скорость изменения координаты тела, поэтому является первой производной функции
характеризует скорость изменения координаты тела, поэтому является первой производной функции  по времени:
по времени: 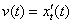 . Если бы в природе не существовало понятия «движение тела», то не существовало бы и производного понятия «скорость тела».
. Если бы в природе не существовало понятия «движение тела», то не существовало бы и производного понятия «скорость тела».
Ускорение тела  – это скорость изменения скорости, поэтому:
– это скорость изменения скорости, поэтому:  . Если бы в природе не существовало исходных понятий «движение тела» и «скорость движения тела», то не существовало бы и производного понятия «ускорение тела».
. Если бы в природе не существовало исходных понятий «движение тела» и «скорость движения тела», то не существовало бы и производного понятия «ускорение тела».
Откуда взялись правила дифференцирования и таблица производных? Невероятно, но все они появились благодаря единственной формуле:  .
.
Пример 1
Используя определение производной, доказать, что производная константы равна нулю.
Функция-константа имеет вид  , и графически – это семейство прямых, параллельных оси абсцисс. Наверное, многие уже догадались, почему
, и графически – это семейство прямых, параллельных оси абсцисс. Наверное, многие уже догадались, почему  .
.
Изобразим, например, график функции  :
:

Это «ровная дорога», то есть функция и не возрастает и не убывает в каждой точке. Ни вверх и не вниз.
Покажем аналитически, что производная функции-константы равна нулю. Рассмотрим произвольное значение  , в котором, понятно,
, в котором, понятно,  . Придадим аргументу приращение:
. Придадим аргументу приращение:  . Функция всё время постоянна, поэтому
. Функция всё время постоянна, поэтому  и приращение функции:
и приращение функции:  . По определению производной в точке:
. По определению производной в точке:

Заметьте, тут нет неопределённости: ноль, делённый на бесконечно малое число  , равен нулю.
, равен нулю.
Поскольку в качестве точки  можно взять любое «икс», то проведём замену
можно взять любое «икс», то проведём замену  и получим:
и получим:  .
.
Пример 2
Найти производную функции  по определению.
по определению.
Рассмотрим произвольное значение  , в котором
, в котором  .
.
Зададим аргументу приращение  и вычислим соответствующее значение функции:
и вычислим соответствующее значение функции:  (обычная алгебра – в функцию
(обычная алгебра – в функцию  вместо «икса» подставили
вместо «икса» подставили  и раскрыли скобки).
и раскрыли скобки).
Вычислим приращение функции:

По определению производной в точке:

Поскольку в качестве  можно взять любое значение
можно взять любое значение  , то
, то 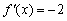 .
.
О чём нам говорит найденная производная? Во-первых, для любого «икс» она отрицательна, а значит, функция  убывает на всей области определения. И, во-вторых, это убывание постоянно, то есть «наклон горки везде одинаков» – в какой бы точке мы ни находились, предельное отношение
убывает на всей области определения. И, во-вторых, это убывание постоянно, то есть «наклон горки везде одинаков» – в какой бы точке мы ни находились, предельное отношение 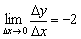 будет неизменным:
будет неизменным:

Здесь и далее я предполагаю, что читатель умеет находить, как минимум, простые производные, пользуясь правилами дифференцирования и таблицей. Давайте найдём производную «быстрым» способом: 
Используя этот же алгоритм, можно решить задачу в общем виде и доказать, что производная линейной функции  равна её угловому коэффициенту:
равна её угловому коэффициенту:
 .
.
Касательная к графику линейной функции в каждой точке совпадает с самим графиком данной линейной функции.
Пример 3
Найти производную функции  по определению.
по определению.
Рассмотрим произвольную точку  и соответствующее значение
и соответствующее значение  . Зададим приращение
. Зададим приращение  и вычислим значение функции в точке
и вычислим значение функции в точке  :
:
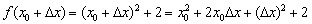
Найдём приращение функции:

По определению производной в точке:

Поскольку в качестве  можно рассмотреть любую точку
можно рассмотреть любую точку  области определения функции
области определения функции  , то проведём замену
, то проведём замену  и получим
и получим  .
.
Проверим результат, используя таблицу производных: 
Исходная функция  и её производная
и её производная  – это две совершенно разные функции, однако между ними существует чёткая и прозрачная связь:
– это две совершенно разные функции, однако между ними существует чёткая и прозрачная связь:

На интервале  производная отрицательна:
производная отрицательна:  (красная линия), что говорит об убывании функции
(красная линия), что говорит об убывании функции 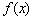 на данном интервале. Грубо говоря, ветвь параболы идёт сверху вниз. А на интервале
на данном интервале. Грубо говоря, ветвь параболы идёт сверху вниз. А на интервале  производная положительна:
производная положительна: 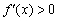 (зелёная линия), значит, функция
(зелёная линия), значит, функция 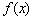 растёт на этом интервале, и её график идёт снизу вверх.
растёт на этом интервале, и её график идёт снизу вверх.
При  производная равна нулю:
производная равна нулю:  . Найденное значение показывает, что скорость изменения функции
. Найденное значение показывает, что скорость изменения функции  в точке
в точке  равна нулю (функция не растёт в ней и не убывает). В данном случае здесь минимум функции.
равна нулю (функция не растёт в ней и не убывает). В данном случае здесь минимум функции.
Всё это можно утверждать даже не зная, что такое парабола и как выглядит график функции  !
!
И ещё раз заостряю внимание, что значение производной в точке выражает собой некоторую меру скорости изменения функции в данной точке. Найдём несколько значений производной:

Таким образом, в точке  функция
функция  убывает, в точке
убывает, в точке  сохраняет скорость постоянной, а в точках
сохраняет скорость постоянной, а в точках  – растёт. Причём
– растёт. Причём  , поэтому можно сказать (опять даже не зная чертежа!), что в окрестности точки
, поэтому можно сказать (опять даже не зная чертежа!), что в окрестности точки  график функции
график функции  идёт вверх круче, чем вблизи точки
идёт вверх круче, чем вблизи точки  .
.
Закрепим геометрический смысл: производная в точке численно равна тангенсу угла наклона касательной к графику функции в данной точке. Применим формулу 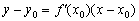 четыре раза:
четыре раза:
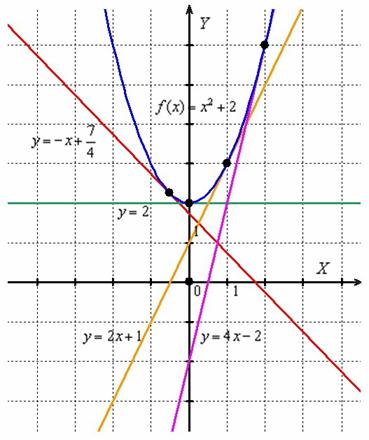
Вот так изящно производная характеризует свою функцию.