Перпендикулярность прямых и плоскостей в пространстве

Контрольная работа

Часть 1. Выберите один правильный ответ (1 балл) и впишите его в бланк внизу заданий (перерисуйте в тетрадь!).

Параллельность прямых и плоскостей в пространстве

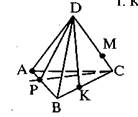
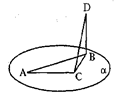
А1 Какой плоскости не принадлежит точка А? (рис. 1)

А) DАВ В) DСА С) АРС Д) ВDС

А2 На каких плоскостях лежит прямая DB? (рис. 1)

А) АDC и ADB В) ADB и ABC С) ADB и DCB Д) DKB и DCA

A3 В какой точке пересекаются прямая PC и плоскость ADB? (рис. 1)

А) Р В) С С) А Д) D

A4 По какой прямой пересекаются плоскости AВС и ADC? (рис. 1)

А) DВ В) DС С) АС Д) ВA

A5 Какие прямые лежат в плоскости BDC? (рис. 1)

А) DB, AC,DK. AB В) KB, DA,DK. CP С) DP, DC,DK. CA Д) DB, DC,DK. CB

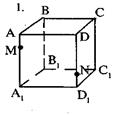
А6 Укажите точку пересечения прямой MD с плоскостью ABC (рис. 2)

А) D В) С С) А Д) M

А7 Укажите прямую пересечения плоскостей АВС и АВВ₁ (рис. 2)

А) DВ В) DС С) ВС Д) AВ

А8 Плоскости α и β пересекаются по прямой с. Выберите верную запись:

А) α × β= с В) α ∩ β= с С) α ║ β= с Д) α ∩ β= С

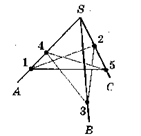
А9 Туго натянутая нить закреплена в точках 1,2,3,4,5, расположенных на стержнях SA,SB,SC. Укажите количество точек, в которых отрезки нити соприкасаются (рис. 3)

А) 0 В) 1 С) 2 Д) 3

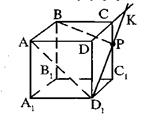
А10 Как располагаются прямые AD₁ и D₁C₁? (рис. 4)

А) параллельны В) пересекаются С) перпендикулярны

А11 Найдите угол между прямыми AD₁ и ВВ₁ (рис. 4)

А) 180º В) 60 ºС) 90 º Д) 45 º

А12 Найдите точку пересечения прямых DC и CC₁ (рис. 4)

А) D В) С С) А Д) К

А13 Найдите рёбра, параллельные грани АВВ₁А₁ (рис. 4)

А) АD, ВC, A₁ D_1, B₁С₁ В) АВ, ВC, A₁ D_1, B₁С₁С) DD₁, CC₁, C₁ D_1, DС

Перпендикулярность прямых и плоскостей в пространстве

А14 Укажите рёбра, перпендикулярные плоскости АВВ₁ (рис. 4)

А) DА, ВC,СС₁, AB В) СB, DA,D₁А₁, C₁А₁ С) DС, ВC,DА, C ₁В₁

А15 Выберите верное утверждение (рис. 4)

А) AD║ BA В) AB D ₁С₁ С) DC ║ BC Д) DС BC

А16 Как расположены друг к другу рёбра куба, выходящие из одной вершины?

А) Перпендикулярны В) Параллельны

А17 Отрезок ВD перпендикулярен плоскости α. СD является: (рис. 5)

А) Перпендикуляром В) Наклонной С) Проекцией наклонной

А18 Укажите общий перпендикуляр для прямых AD и CC₁ (рис. 4)

А) DС В) СА С) DD₁ Д) ВС

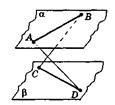А19 Плоскости α и β параллельны. Каково взаимное расположение прямых AD и BC? (рис. 6)

А) Пересекаются В) Скрещиваются

А20 Прямые a и b параллельные и лежат в плоскости α. Через каждую из этих прямых проведена плоскость, перпендикулярная α. Каково взаимное расположение полученных плоскостей?

А) Пересекаются В) Скрещиваются С) Параллельны Д) Совпадают

Часть 2. Сделайте рисунок (1 балл) и запишите решение задачи (2 балла).

В1 Через концы отрезка MN и его середину К проведены параллельные прямые, пересекающие плоскость α в точках M _1, , N₁ и К₁ . Найдите длину отрезка КК₁, если отрезок MN не пересекает α и ММ₁ = 6 см, NN₁= 2 см.

В2 Даны две параллельные плоскости. Через точки А и В одной из плоскостей проведены две параллельные прямые до пересечения в точках А₁ и В₁. Найдите длину отрезка А₁ В₁ если АВ=10 см.

В3 Из точки М проведены к плоскости α до пересечения в точках N и К два отрезка. Точки D и Е – середины отрезков MN и МК. Найдите длину отрезка NК, если DЕ = 4 см.

В4 Через вершину острого угла прямоугольного треугольника АВС с прямым углом С проведена прямая АD, перпендикулярная плоскости треугольника. Чему равно расстояние от точки D до вершины С, если АС = 6 см; АD = 8 см.

В5 Наклонная равна 2 см. Чему равна проекция этой наклонной на плоскость, если наклонная составляет с плоскостью угол равный 45 º?

В6 Отрезки двух наклонных, проведённые из одной точки до пересечения с плоскостью, равны 15 и 20 см, проекция одного из отрезков равна 16 см. Найдите проекцию другого отрезка.

В7 Дан куб АВСDА₁В₁С₁D_1.. Чему равен угол между плоскостью А₁В₁С₁D₁ и плоскостью проходящей через прямые А₁В₁и СD?