Приведение силы к заданному центру
Дано:
 приложена в точке А.
приложена в точке А.
Приведем  к произвольному центру О.
к произвольному центру О.
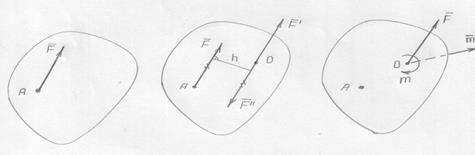
а) б) перенесём  в в) получили:
в в) получили:
точку О и силу и пару
добавим  .
. 
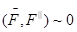
 - приведенная сила
- приведенная сила

 -присоединенная пара
-присоединенная пара
 или
или 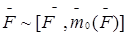 ,
,
Данная сила эквивалентна совокупному действию приведенной силы и присоединенной пары. Причем, приведённая сила геометрически равна заданной и приложена в произвольном центре, а момент присоединенной пары равен моменту данной силы относительно того же центра.
Приведение произвольной системы сил к заданному центру
Пусть дана некоторая произвольная система сил 
Приведем эту систему сил к произвольному центру О.


Сложим геометрически все приведенные силы  ;
;

- главный вектор системы сил.
Сложим геометрически все присоединенные пары  ;
;


Любая произвольная система сил в общем случае эквивалентна силе, называемой главным вектором системы, равным геометрически сумме сил заданных, и паре сил с моментом, называемым главным моментом системы сил, равной геометрически сумме моментов всех сил относительно центра приведения.
Замечание. Не следует отождествлять главный вектор  с равнодействущей
с равнодействущей 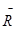 , т.к равнодействующая – это одна сила, эквивалентная данной системе сил, а главный вектор эквивалентен данной системе сил только в совокупности с парой сил, момент который равен главному моменту
, т.к равнодействующая – это одна сила, эквивалентная данной системе сил, а главный вектор эквивалентен данной системе сил только в совокупности с парой сил, момент который равен главному моменту  .
.
Главный вектор системы не зависит от центра приведения, а главный момент существенно зависит от центра приведения.
Главный вектор определим из выражений
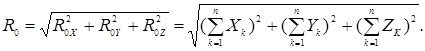


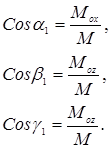
Приведение системы сил к простейшему виду
В результате приведения системы сил к данному центру могут встретиться следующие слечаи:
1.  - общий случай,
- общий случай,
2.  - случай равновесия,
- случай равновесия,
3.  - система сил приводится к равнодействующей,
- система сил приводится к равнодействующей,
4.  - система сил приводится к паре.
- система сил приводится к паре.
Условия равновесия произвольной системы сил в векторной форме
Для равновесия произвольной системы сил необходимо и достаточно, чтобы одновременно выполнялись условия:
 .
.
Но 

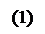

Таким образом при равновесии произвольной системы сил геометрическая сумма всех сил и моменты этих сил относительно любого центра равны О, т.е силовой и моментный многоугольники замкнуты.

Аналитические условия равновесия произвольной плоской системы сил
Для плоской системы сил (1) можно представить в виде:

 (1’)
(1’)
Т.к. вектора  перпендикулярны плоскости дейтвия сил, то их сумму можно представить алгебраической суммой.
перпендикулярны плоскости дейтвия сил, то их сумму можно представить алгебраической суммой.
Проецируя выражение главного вектора (1’) на оси координат и оставляя неизменным выражение главного момента, получим так называемую основную форму условий равновесия произвольной плоской системы сил:

Читать. Для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы алгебраическая сумма проекций всех сил на каждую из двух координатных осей и алгебраическая сумма их моментов относительно любой точки, лежащей в поскости действия сил, равнялись нулю.
Существуют еще две эквивалентные формы неоходимых и достаточных условий равновесия:
в виде теоремы о трех моментах и третьей формы условия равновесия:


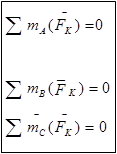
(II)

Пример 1
 Дано:
Дано:
F=10H

M=8Hм
q=6Н/м
a=0.4м
b=0.6 
Найти:
Равномерно распределенную нагрузку заменим сосредоточенной силой
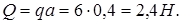
Для произвольной плоской системы сил составим 3 уравнения равновесия:

 (1)
(1)
 , (2)
, (2)
 (3) Из уравнений (1) - (3) находим искомые реакции
(3) Из уравнений (1) - (3) находим искомые реакции
 (1)
(1) 
 (2)
(2) 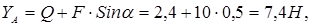
 (3)
(3) 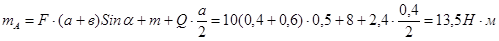
Пример 2

| 
|
 Пространственная система сил
Пространственной называется система сил расположенная в пространстве.
Момент силы относительно оси
Пространственная система сил
Пространственной называется система сил расположенная в пространстве.
Момент силы относительно оси
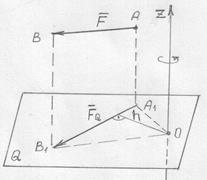 Чтобы вычислить момент силы
Чтобы вычислить момент силы  относительно оси Z, следует спроецировать эту силу на плоскость Q, перпендикулярную оси, а затем вычислить момент этой проекции относительно оси Z, следует спроецировать эту силу на плоскость Q, перпендикулярную оси, а затем вычислить момент этой проекции  относительно точки О пересечения оси с плоскостью.
Определение. Моментом силы относительно оси называют алгебраический момент проекции этой силы на плоскость, перпендикулярную оси, относительно точки пересечения оси с плоскостью относительно точки О пересечения оси с плоскостью.
Определение. Моментом силы относительно оси называют алгебраический момент проекции этой силы на плоскость, перпендикулярную оси, относительно точки пересечения оси с плоскостью
  Правило знаков.
Момент положен, если воображаемое вращение тела под действием проекции силы вокруг оси видно с ее положенного направления происходящим против часовой стрелки.
Момент силы относительно оси характеризует меру вращательного эффекта силы вокруг оси.
Правило знаков.
Момент положен, если воображаемое вращение тела под действием проекции силы вокруг оси видно с ее положенного направления происходящим против часовой стрелки.
Момент силы относительно оси характеризует меру вращательного эффекта силы вокруг оси.
 
    т.е.ось и сила лежат в одной плоскости.
Зависимость между моментом силы относительно центра и оси
Установим зависимость между моментом силы относительно точки и моментом силы относительно оси, проходящей через эту точку. т.е.ось и сила лежат в одной плоскости.
Зависимость между моментом силы относительно центра и оси
Установим зависимость между моментом силы относительно точки и моментом силы относительно оси, проходящей через эту точку.
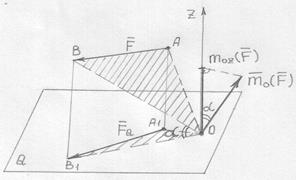 Ранее установлено, что
Ранее установлено, что
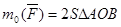
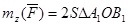 Т.к.
Т.к.  , является проекцией , является проекцией  на плоскость Q, то на плоскость Q, то
 (1)
Умножив обе части (1) на 2, получим: (1)
Умножив обе части (1) на 2, получим:
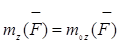  или или 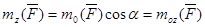 ,
Аналитические выражения моментов
силы относительно координатных осей ,
Аналитические выражения моментов
силы относительно координатных осей
 Дано: Дано:  . Найти аналитические выражения моментов силы . Найти аналитические выражения моментов силы  относительно осей координат.
Изобразим декартову систему координат и покажем относительно осей координат.
Изобразим декартову систему координат и покажем  ; ;
 -координаты точки приложения силы, -координаты точки приложения силы,
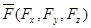 - проекции силы - проекции силы  на оси координат.
Если дана сила на оси координат.
Если дана сила  (известны ее проекции на оси координат) и даны координаты x,y,z точки приложения этой силы, то векторный момент относительно начала координат (известны ее проекции на оси координат) и даны координаты x,y,z точки приложения этой силы, то векторный момент относительно начала координат 
 после разложения по координатным осям можно представить определителем третьего порядка после разложения по координатным осям можно представить определителем третьего порядка



   = =  . .
 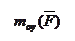  Выражения в скобках определяют проекции вектора Выражения в скобках определяют проекции вектора  на оси координат.
Используя зависимость между моментом силы относительно центра и оси, получим на оси координат.
Используя зависимость между моментом силы относительно центра и оси, получим
 -аналитические выражения моментов силы относительно координатных осей.
Аналитические условия равновесия произвольной пространственной системы сил
В геометрической форме
-аналитические выражения моментов силы относительно координатных осей.
Аналитические условия равновесия произвольной пространственной системы сил
В геометрической форме  и и 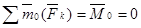 . (1) . (1)
  Аналитическая форма условий равновесия получается, если спроецировать (1) на координатные оси:
Читать. Для равновесия произвольной пространственной системы сил необходимо и достаточно, чтобы алгебраические ∑ проекций всех сил на каждую из трех координатных осей и ∑ моментов сил относительно этих осей равнялись нулю. Аналитическая форма условий равновесия получается, если спроецировать (1) на координатные оси:
Читать. Для равновесия произвольной пространственной системы сил необходимо и достаточно, чтобы алгебраические ∑ проекций всех сил на каждую из трех координатных осей и ∑ моментов сил относительно этих осей равнялись нулю.
|