Простейшие движения твердого тела
В ТМ различают 5 видов движения: поступательное, вращательное, плоское (плоскопараллельное), сферическое, общий случай движения.
Поступательное движение твердого тела
Поступательным называется такое движение твердого тела, при котором всякая прямая, взятая в теле, остается параллельной своему начальному направлению.

Теорема. При поступательном движении твердого тела все его точки
1). Описывают тождественные и параллельные траектории и
2). Имеют геометрически равные скорости и ускорения.
Изобразим тело, совершающее поступательное движение, в моменты времени t и t’. Проведем в теле прямую АВ, согласно определению она останется параллельной своему начальному направлению.

 Для любого момента времени
Для любого момента времени

 . (1)
. (1)
1).Тождественность и параллельность очевидны, т.к. в любом положении твердого тела точка В сдвинута по отношению к А на вектор  .
.
2).Продифференцируем (1) по времени:
 ;
; 

Продифференцировав еще раз по времени, имеем

Т.о. доказана вторая часть теоремы.
Вывод. Изучение поступательного движения тела сводится к изучению движения любой его точки (обычно - центра тяжести), т.е. поступательно движущееся тело можно рассматривать как геометрическую точку.
Вращение твердого тела вокруг неподвижной оси
Вращательным называется движение твердого тела, при котором все его точки описывают окружности с центрами на одной и той же неподвижной прямой (ось вращения), перпендикулярной их плоскостям вращения.
Уравнение вращательного движения 
 -угол поворота.
-угол поворота.
Угловая скорость и угловое ускорение (вращающегося твердого тела)
Угловой скоростью называется пространственно-временная мера вращения, характеризующая изменение угла поворота твердого тела.

Р. - неподвижная плоскость.
|
 Q
Q 
Q1 
 -средняя угловая скорость
-средняя угловая скорость


Читать. Угловая скорость в данный момент времени равна первой производной от угла поворота по времени.

Угловым ускорением называется пространственно-временная мера вращения твердого тела, характеризующая изменение угловой скорости.
Пусть 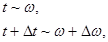
 - среднее угловое ускорение
- среднее угловое ускорение


Читать. Угловое ускорение в данный момент времени равно первой производной от угловой скорости или второй производной от угла поворота по времени.

 и
и  характеризует вид вращения:
характеризует вид вращения:
· Равномерное (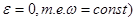 ;
;
· Ускоренное  и
и  одного знака
одного знака  ;
;
· Замедленное  и
и  имеют противоположные знаки).
имеют противоположные знаки).
Частные случаи вращательного движения
1. Равномерное вращение 

 .
.
Н.у. При  . Тогда
. Тогда
2. Равнопеременное вращение 

 .
.
Н.у. При  . Тогда
. Тогда
Найдем изменения угла поворота
 .
.
Н.у. при  . Тогда
. Тогда 
Замечание: 1.В технике часто используется число
оборотов-N(1 об.= 2  рад)
рад)

2.При вращении, где n[об/мин] частота вращения

Скорость и ускорение (линейные) точек вращающегося твердого тела
 Дано:
Дано:



 Уравнение движения точки по траектории:
Уравнение движения точки по траектории:
 ,
,  .
.
Для скорости
 .
.

 направлен по касательной к окружности (в точке касания он
направлен по касательной к окружности (в точке касания он  радиусу).
радиусу).
Т.к. точка М совершает криволинейное движение (перейдем к естественному способу)
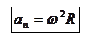




Т.к.  , то
, то 

Радиус, образованный вектором  с радиусом
с радиусом 


Векторные выражения угловой скорости и углового ускорения

|

|

Если примем ось вращения тела за ось Z и обозначим через  орт этот оси, то
орт этот оси, то
 ,
,  . (1)
. (1)
Вектор  направлен вдоль оси вращения в ту сторону, откуда вращения
направлен вдоль оси вращения в ту сторону, откуда вращения
видно происходящим против часовой стрелки.
Продифференцируем (1) по времени:

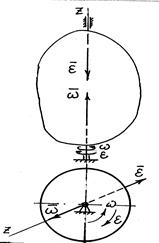
 Вектор
Вектор  направлен вдоль вращения либо в сторону
направлен вдоль вращения либо в сторону 
 (ускоренное вращение), либо в противоположную сторону (замедленное вращения).
(ускоренное вращение), либо в противоположную сторону (замедленное вращения).
 и
и  - вектора скользящие, т.е. могут быть приложены к любой точке оси вращения.
- вектора скользящие, т.е. могут быть приложены к любой точке оси вращения.
Векторные выражения линейных скорости и ускорения

Покажем, что  (формула Эйлера).
(формула Эйлера).
Рассмотрим вращение точки М. Из производной точки О, лежащей на оси вращения, проводим вектор  и радиус-вектор
и радиус-вектор 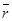 точки М.
точки М.


 .
.



Правая часть представляет модуль векторного произведения формулы Эйлера.
Покажем, что вектора  и
и  имеют одинаковое направление.
имеют одинаковое направление.
Согласно свойству векторного произведения вектор  плоскости, образованный векторами – сомножителями, и направлен в ту сторону, откуда поворот от первого сомножителя ко второму на кратчайший угол виден происходящим против часовой стрелки.
плоскости, образованный векторами – сомножителями, и направлен в ту сторону, откуда поворот от первого сомножителя ко второму на кратчайший угол виден происходящим против часовой стрелки.
Следовательно, модули равны, а вектора коллинеарны и направлены в одну сторону, т. е. действительно
 |
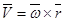 (1) Вектор
(1) Вектор  направлен по касательной к
направлен по касательной к
траектории ( R) в сторону дуговой стрелки
R) в сторону дуговой стрелки
 .
.
Продифференцируем (1) по времени


 Модули
Модули 
 |
 Вектор
Вектор  направлен по касательной к траектории (
направлен по касательной к траектории ( R) в сторону дуговой стрелки
R) в сторону дуговой стрелки  .
.

 Вектор
Вектор  направлен по радиусу к центру (оси) вращения.
направлен по радиусу к центру (оси) вращения.
Задача. При пуске в ход машины для кручения нити веретено диаметром 40 мм приобретает рабочую скорость 1800об/мин за 30 сек.
Определить: 1).Число оборотов шпинделя до полного разгона и скорость точек внешней поверхности бобины, если ее диаметр 20 мм;
2).Скорость бобины; скорость и ускорение точек поверхности через 10 сек после начала вращения.
 Дано:
Дано:

Найти:
 при
при 
 при
при 
Решение.
1. 


 .
.

 м/с
м/с




0 0
 об
об
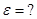

|

|
|
|
|
|

