Плоским называется движение твердого тела, при котором все его точки движутся плоскостях, параллельных некоторой неподвижной плоскости.
Рассмотрим плоскопараллельное движение твердого тела.
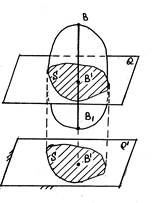
Рассечем тело плоскостью 
Возьмем в теле прямую  плоскости
плоскости  .
.
Т.к. по определению все точки движутся в плоскостях параллельных неподвижной плоскости,  будет все время параллельна первоначальному направлению (по определению это поступательное движение).
будет все время параллельна первоначальному направлению (по определению это поступательное движение).

 т.к. отрезок ВВ1 совершает поступательное движение.
т.к. отрезок ВВ1 совершает поступательное движение.
Т.е. задача изучения плоского движения сводится к изучению движения сечения S в его плоскости.
Сечение S будем называть в дальнейшем плоской (неизменяемой) фигурой.
Уравнение движения плоской фигуры. Разложение движения плоской фигуры на поступательное и вращательное

Пусть тело совершает плоское движение.
Выберем систему координат, жестко связанную с плоской фигурой.
Из аналитической геометрии известно, что для определения положения системы относительно неподвижных осей координат необходимо знать  - обобщенные координаты плоской фигуры S.
- обобщенные координаты плоской фигуры S.
Уравнения движения плоскости являются функции вида:


 определяют поступательное движение
определяют поступательное движение
определяет вращательное движение.
Т.о. всякое абсолютное движение плоской фигуры можно разложить на поступательное (переносное) вместе с произвольно выбранной точкой (О), называемой полюсом, и на вращательное (относительное) вокруг этого полюса.
При этом поступательная часть зависит от выбора полюса, а вращательная часть не зависит от выбора полюса.
Теорема о независимости закона вращательной части плоской фигуры от выбора полюса
Теорема. Закон вращательной части плоской фигуры не зависит от выбора полюса.
Пусть плоская фигура переместилась из положения 1 в положение 2.

Полюс А. Переносное движение поступательное до совмещения А с А1.
Относительное движение- поворот вокруг полюса А 1 отрезка В’А1 до совмещения В’ с В 1 на  по часовой стрелке.
по часовой стрелке.
Полюс В. Переносное движение поступательное до совмещения т. В’ с В1А1.
Относительное движение - поворот вокруг полюса В1 отрезка А ’ с на  по часовой стрелке.
по часовой стрелке.
Т.о.  (1)
(1)
Следствие. Угловая скорость и угловое ускорение плоской фигуры во вращательной части также не зависят от выбора полюса.
Продифференцируем (1) по времени




В дальнейшем 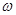 и
и  будем называть угловой скоростью и угловым ускорением плоской фигуры.
будем называть угловой скоростью и угловым ускорением плоской фигуры.
Скорость точки плоской фигуры и разложение её на поступательную и вращательную
Пусть тело совершает плоское движение. Известны скорость некоторой точки и угловая скорость плоской фигуры. Найти скорость произвольной точки М.
 Дано:
Дано:  .
.
 , (1)
, (1)

 т.к. переносное движение поступательное,
т.к. переносное движение поступательное,
 - скорость полюса,
- скорость полюса,
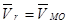 -относительная скорость (скорость точки М
-относительная скорость (скорость точки М
во вращении вокруг полюса).

 Т.о. (1) примет вид
Т.о. (1) примет вид 
Читать. Скорость любой точки плоской фигуры равна геометрической сумме скорости полюса и скорости точки во вращательном движении вокруг этого полюса.
Замечание. За полюс можно принимать любую точку. В практических задачах за полюс удобно принять точку скорость которой известна или её можно непосредственно определить по исходным данным.
Теорема о проекциях скоростей двух точек плоской фигуры на ось, проходящую через эти точки

Дано: 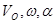
Теорема. Проекции скоростей двух точек плоской фигуры на ось (прямую), проходящую через эти точки, равны.
Примем точку А за полюс, тогда
 . (1)
. (1)
Спроецируем (1) на ось Х прямую AB: 
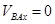 , тогда
, тогда

Что и требовалось доказать.
Мгновенный центр скоростей (МЦС) плоской фигуры и теорема о его существовании
МЦС плоской фигуры называют ту её точку, скорость которой в данное мгновение равна О.
Теорема. При непоступательном движении плоской фигуры в её плоскости МЦС существует в каждый момент времени.
 Дано:
Дано: 
Рассмотрим движение плоской фигуры. Повернём вектор  в сторону вращения плоской фигуры на
в сторону вращения плоской фигуры на  . На полученной полупрямой отложим отрезок
. На полученной полупрямой отложим отрезок  .
.
Покажем, что точка  является МЦС.
является МЦС.
 . (1)
. (1)
 и
и 

Кроме того,  направлены в противоположные стороны.
направлены в противоположные стороны.
Модуль  .
.
Следовательно, складывая два равных и противоположно направленных вектора, получаем
 ,
,

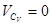 .
.
Замечание. Слово «мгновенный» в определении МЦС подчеркивает то свойство, что эта точка в каждый момент времени располагается в разных местах (в том числе вне плоской фигуры).
Скорость точки плоской фигуры, если за полюс принят МЦС
Дано: 
Найти: 
Примем за полюс
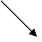

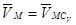
Если за полюс принять МЦС, то скорость любой точки плоской фигуры равна геометрически скорости точки во вращательном движении вокруг МЦС.
Модуль  .(а)
.(а)
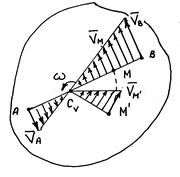 Поле скоростей точек плоской фигуры
Поле скоростей точек плоской фигуры
Если за полюс принять ЦС, то скорость любой точки
 -мгновенный радиус вращения.
-мгновенный радиус вращения.
При вращении вокруг МЦС выполняются соотношения
 .
.
Вывод. Поле распределения скоростей показывает то, что плоская фигура как бы вращается вокруг МЦС в каждый момент времени. При этом скорости точек плоской фигуры пропорциональны расстояниям от точек до МЦС, а вектора скоростей направлены перпендикулярно мгновенным радиусам вращения.
Различные случаи определения МЦС

 1). Из (а)
1). Из (а) 

2). Даны непараллельные прямые вдоль которых могут быть направлены скорости двух точек плоской фигуры. Построить МЦС.
МЦС находится на пересечении перпендикуляров, восстановленных к прямым в точках А и В.

Иногда встречается случай:

Плоская фигура совершает «мгновенно- поступательное движение».
3) Даны параллельные вектора скоростей двух точек плоской фигуры, лежащие на общем перпендикуляре. Определим МЦС.


МЦС находится на пересечении прямой, проведенной через концы векторов, с общим перпендикуляром.
4).Плоская фигура катится без проскальзывания по неподвижному контору. Определить МЦС.
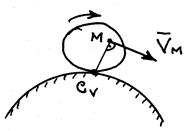
МЦС - в точке контакта контуров.
Пример.
Построить МЦС звена АВ (плоской фигуры АВ).
|
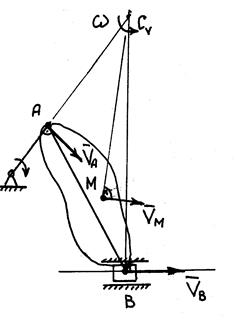
Задача. Груз K,связанный посредствам нерастяжимой нити с катушкой L, опускается вертикально вниз по закону  , при этом катушка L катится по неподвижному рельсу без скольжения. Определите скорости точек C,A,B,O,E катушки в момент времени
, при этом катушка L катится по неподвижному рельсу без скольжения. Определите скорости точек C,A,B,O,E катушки в момент времени  в положении указанном на рисунке, а также угловую скорость катушки, если
в положении указанном на рисунке, а также угловую скорость катушки, если  , а
, а  .
.
Дано:


Определить:
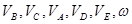
Решение
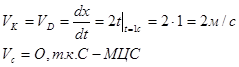
Примем за полюс МЦС.
Тогда скорость произвольной точки М

 и
и 

Скорости всех точек найдем как во вращательном движении (вращением вокруг МЦС):

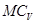 в сторону вращения плоской фигуры, показываем вектор скорости точки М.
в сторону вращения плоской фигуры, показываем вектор скорости точки М.