ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №4
Показатели вариации
Понятие вариации в статистике
При изучении явлений и процессов общественной жизни статистика встречается с разнообразной вариацией. Вариация – это несовпадение уровней одного и того же признака у разных объектов. Вариация имеет объективный характер и помогает познать сущность изучаемого явления.
Вариация порождается комплексом условий, действующих на совокупность и ее единицы. Например, вариация оценок на экзамене в вузе порождается: различными способностями, различием социально-бытовых условий, знаниями, полученными в школе и т.д. Чем больше различия между значениями факторов, тем больше вариация в уровне оценок.
Изменение вариации дает возможность оценить степень воздействия на данный признак других варьирующих признаков, установить какие факторы и в какой степени влияют на исследуемое явление.
Средняя величина — это абстрактная, обобщающая характеристика признака изучаемой совокупности, но она не показывает строения совокупности, которое весьма существенно для анализа. Средняя величина не дает представления о том, как отдельные значения изучаемого признака группируются вокруг средней, сосредоточены ли они вблизи или значительно отклоняются от нее. В том случае, когда индивидуальные значения признака отклоняются от средней незначительно, говорят о типичности средней величины.
Термин "вариация" произошел от латинского «variatio» - изменение, колеблемость, различие. Однако не всякие различия принято называть вариацией. Под вариацией в статистике понимают такие количественные изменения величины исследуемого признака в пределах однородной совокупности, которые обусловлены перекрещивающимся влиянием различных факторов. Различают вариацию признака: случайную и систематическую.
Систематическая вариация признака порождается влиянием основных (факторных) признаков для данной совокупности.
Случайная вариация обусловлена влиянием случайных факторов.
По степени вариации можно судить о следующих сторонах развития изучаемых явлений: об однородности совокупности; об устойчивости индивидуальных значений признака, о типичности средней; о взаимосвязи между признаками одного явления и разных явлений.
Чем однороднее состав совокупности, тем более близки между собой отдельные значения признака и тем меньше разбрасываемость этих значений вокруг средней величины.
При характеристике колеблемости признака применяют систему абсолютных и относительных показателей вариации.
Абсолютные показатели вариации
Для характеристики колеблемости признака используется ряд показателей. Наиболее простой из них - размах вариации.
1. Размах вариации (R) – это разность между максимальным (хmax) и минимальным (хmin) наблюдаемыми значениями признака:
R= хmax- хmin
(5.1)
Отметим, что размах вариации характеризует лишь максимальное различие значений признака и не может измерять закономерную силу его вариаций во всей совокупности.
Более строгими характеристиками являются показатели его колеблемости относительно среднего уровня признака. Для многих варьирующих признаков возможно допущение, что при прочих равных условиях все единицы совокупности в соответствии с основными законами своего развития имели бы одинаковую и притом вполне определенную величину признака в данных условиях места и времени. В качестве такой величины условно принимают среднюю из всех значений признака, поскольку в ней частично погашаются случайные отклонения от закономерного хода развития явлений. Средняя величина тем самым отражает типичный размер признака у данной однородной совокупности единиц. Но условия существования и развития отдельных единиц совокупности в определенной степени различны, что сказывается на различии значений у исследуемого признака. Средняя величина отражает эти средние условия.
Таким образом, средняя применяется в качестве своего рода центра тяжести, вокруг которого происходят колебание, рассеяние значений признака. При обобщении этих колебаний необходимо вновь прибегнуть к методу средних величин – найти среднюю величину этих отклонений.
2. Среднее линейное отклонение (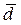
) -это среднее арифметическое значение абсолютных отклонений признака от его среднего уровня. Показывает, насколько в среднем, отклоняется признак в изучаемой совокупности от среднего значения (т.е. насколько средняя величина типична для данной совокупности). Определяется по формуле:
ü для несгруппированных данных: 
;
ü для вариационного ряда: 
(5.2)
Простота расчета и интерпретации составляет положительные стороны данного показателя. Он нашел широкое применение на практике. С его помощью анализируется, например, состав работающих, ритмичность производства, равномерность поставок, разрабатываются системы материального стимулирования. Но математические свойства модулей усложняют расчеты вероятностного типа, затрудняет применение методов математической статистики. Поэтому в статистических научных исследованиях для измерения вариации чаще всего применяют показатель дисперсии.
3. Дисперсия (σ2) представляет собой средний квадрат отклонений индивидуальных значений признака от их средней величины. Определяется по формуле:
ü для несгруппированных данных: 
;
ü для вариационного ряда:. 
(5.3)
Формула для расчета дисперсии может быть преобразована и получена формула расчета дисперсии методом моментов:
(5.4)
где 
среднее значение квадратов признака, или начальный момент второго порядка;
- среднее значение признака, или начальный момент первого порядка.
Величина дисперсии признака σ2 носит еще название центрального момента второго порядка.
Формула метода моментов используется довольно часто. На ней основываются, например, методы статистического имитационного моделирования, а также, если первичные данные сгруппированы, метод моментов позволяет ускорить расчет дисперсии по аналогии с расчетом среднего значения.
Свойства дисперсии.
Уменьшение или увеличение весов (частот) варьирующего признака в определенное число раз дисперсии не изменяет.
Уменьшение или увеличение каждого значения признака на одну и ту же постоянную величину А дисперсии не изменяет.
Уменьшение или увеличение каждого значения признака в какое-то число k раз соответственно уменьшает или увеличивает дисперсию в 
раз, а среднее квадратическое отклонение - в k раз.
Дисперсия признака относительно произвольной величины всегда больше дисперсии относительно средней арифметической на квадрат разности между средней и произвольной величиной: 
. Если А равна нулю, то приходим к следующему равенству: 
, т.е. дисперсия признака равна разности между средним квадратом значений признака и квадратом средней.
Каждое свойство при расчете дисперсии может быть применено самостоятельно или в сочетании с другими.
4. Среднее квадратическое отклонение (σ) равно корню квадратному из суммы квадратов отклонений индивидуальных значений признака от их средней.
Определяется по формуле:
ü для несгруппированных данных: 
;
ü для вариационного ряда: 
(5.5)
Рассмотренные абсолютные показатели вариации выражаются в единицах измерения вариационного признака, с их помощью можно сравнивать вариацию только одного и того же признака в распределениях.
Для оценки интенсивности вариации и для сравнения ее в разных совокупностях, для сравнения вариации разных признаков необходимы относительные показатели вариации. Они вычисляются как отношения абсолютных показателей вариации к средней арифметической величине признака.
Различают следующие относительные показатели вариации:
ü коэффициент осцилляции (отношение размаха вариации (R) к средней арифметической величине (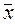
):
;
(5.6)
ü линейный коэффициент вариации (отношение среднего линейного отношения (
) к средней арифметической величине ()):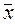
;
(5.7)
ü коэффициент вариации (отношение среднеквадратического отклонениния (σ) к средней арифметической величине ():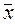
(5.8)
Чаще всего относительные показатели вариации выражаются в процентах и определяют не только сравнительную оценку вариации, но и дают характеристику однородности совокупности. Если коэффициент вариации не превышает 33%, то совокупность считается однородной, а среднее значение признака 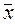является величиной типичной для данной совокупности.
Рассмотрим пример расчета показателей вариации. Распределение студентов по возрасту одного факультета характеризуется следующими данными:
| Возраст студента, лет | ||||||||
| Число студентов |
Размах вариации для данной совокупности составляет 7 лет (24-17).
Средний возраст студента найдем по формуле арифметической взвешенной:
Для расчета показателей вариации построим технологическую таблицу.
Таблица 5.1
Технологическая таблица
| х | Итого | ||||||||
| f | |||||||||
| |||||||||
| 304,2 | 672,8 | 324,9 | 89,1 | 1,3 | 205,7 | 396,9 | 576,6 | 2571,5 |
Используя формулы, приведенные в данной главе рассчитаем:
ü среднее линейное отклонение:
d = 1155/750 ≈1.5 года
ü дисперсию:
σ2 = 2571,5/750 ≈ 3,44 года
ü среднее квадратическое отклонение:
σ = √3,44 ≈ 1,86 года
ü коэффициент вариации:
Vσ = 1.86 *100 / 20.9 ≈ 8.9 %
ü коэффициент осцилляции:
VR = 7 * 100 / 750 = 0.93%
ü линейный коэффициент вариации:
Vd = 1.5*100 / 750 = 7.1%.
Так как коэффициент вариации получился существенно меньше заданного числа (33 %), то можно судить об однородности совокупности и типичности средней величины.