Правило сложения дисперсий

Наряду с изучением вариации признака по всей совокупности в целом часто бывает необходимо проследить количественные изменения признака по группам, на которые разделяется совокупность, а так же и между группами.

Такое изучение вариации достигается посредством вычисления и анализа различных видов дисперсии.

Общая дисперсия (σ₀²) измеряет вариацию признака во всей совокупности под влиянием всех факторов (причин), обусловивших эту вариацию:

;

(5.9)

где х₀ – общая средняя арифметическая для всей изучаемой совокупности.

Межгрупповая дисперсия (δ²) характеризует систематическую вариацию, т.е. различия в величине изучаемого признака, возникающие под влиянием признака – фактора, положенного в основание группировки. Рассчитывается по формуле:

(5.10)

где - средняя по отдельной группе;

- межгрупповая средняя;

n_i - число единиц в определенной группе.

Средняя внутригрупповая дисперсия () отражает случайную вариацию, возникающую под влиянием других, неучтенных факторов и не зависящую от признака – фактора, положенного в основание группировки. Рассчитывается:

или

(5.11)

где - дисперсия по отдельной группе; .

Существует закон (правило сложения дисперсий), связывающий 3 вида дисперсии: величина общей дисперсии равна сумме межгрупповой дисперсии и средней внутригрупповой дисперсии:

σ₀= δ²+

(5.12)

Данное правило широко используется при исчислении показателей тесноты связи, в дисперсионном анализе, при оценке точности типической выборки и в других случаях.

Расчет приведенных видов дисперсий рассмотрим на следующем примере:

По данным выборочного обследования заработной платы работников бюджетной сферы получены следующие показатели:

Отрасль	Средняя з/плата, д.е.	Численность, чел	Дисперсия з/платы, д.е.
Здравоохранение
Образование
Итого

Средняя заработная плата работников по двум отраслям составляет 720д.е.

Зная дисперсию признака в каждой группе, найдем среднюю из внутригрупповых дисперсий:

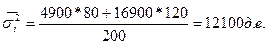
Межгрупповая дисперсия будет составлять 9600 д.е.

Исходя, из правила сложения дисперсий, общая дисперсия равна:

σ² = 9600+12100 = 21700 д.е.

На основе, рассчитанных показателей можно определить, какая доля всей вариации признака обусловлена систематической вариацией, какая случайной, посредством расчета таких показателей как коэффициент детерминации и эмпирическое корреляционное отношение.

Коэффициент детерминации рассчитывается по формуле:

(5.13)

В данном примере η² = (9600/21700)*100 = 44,24 %, следовательно, оплата труда на 44,24 % зависит от отраслевой принадлежности предприятия и на 55,76 % от внутриотраслевых причин.

Эмпирическое корреляционное отношение определяет силу связи между рассматриваемыми признаками и рассчитывается:

(5.14)

Данный показатель изменяется от 0 до 1. Если связь между факторным и результативным признаком отсутствует, то η равно 0, если связь близка к функциональной, то η = 1.

В нашем примере этот показатель равен 66,5 %, что свидетельствует о существенном влиянии отраслевых особенностей на дифференциацию заработной платы.

Для качественной оценки тесноты связи на основе данного показателя можно воспользоваться следующей таблицей: