МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ОБНИНСКИЙ ИНСТИТУТ АТОМНОЙ ЭНЕРГЕТИКИ - филиал
федерального государственного автономного образовательного учреждения
высшего профессионального образования
«Национальный исследовательский ядерный университет «МИФИ»
(ИАТЭ НИЯУ МИФИ)
Факультет Кибернетики
Кафедра Компьютерных систем, сетей и технологий
реферат на тему:
«Линейные блоковые коды»
Выполнил:
Студент
гр. ВТ1-С10
Еличева Е.А.
Проверил:
Мышев А.В.
Обнинск 2013
Содержание
Введение……………………………………………………………..2
Глава 1.Векторное пространство.………………………………..2
Глава 2.Структура линейных блоковых кодов…….………….2
Глава 3.Матричное описание линейных блоковых кодов..….5
Глава 4.Стандартное расположение…………………..………...6
Вывод………………………………………………………..………10
Введение
Управление правильностью передачи информации выполняется с помощью помехоустойчивого кодирования. Есть коды, обнаруживающие ошибки, и корректирующие коды, которые еще и исправляют ошибки. Помехозащищенность достигается с помощью введения избыточности, дополнительных битов.
Простейшими способами обнаружения ошибок являются контрольное суммирование, проверка на нечетность. Однако они недостаточно надежны, особенно при наличии множества ошибок. Поэтому в качестве надежных обнаруживающих кодов применяют линейные коды.
Глава 1. Векторное пространство.
Известный пример векторного пространства дает трехмерное евклидово пространство, фигурирующее во многих физических задачах. Его обобщением является n-мерное векторное пространство над полем вещественных чисел. Понятие n-мерного пространства тесно связано с идеями линейной алгебры и теории матриц и играет важную роль во многих приложениях.
Для произвольного поля можно дать абстрактное определение векторных пространств.
Определение. Пусть F — некоторое поле. Назовем элементы из F скалярами. Множество V называется векторным пространством, и его элементы называются векторами, если для пар элементов из V определена такая операция векторного сложения (обозначается плюсом), а для элементов из V и элементов из F определена такая операция умножения на скаляры, что результат выполнения операции дает элемент из V.
В качестве примера векторного пространства V можно указать множество многочленов от х с коэффициентами из GF (q). Векторами этого пространства служат многочлены. Векторное сложение совпадает со сложением многочленов, а умножение на скаляр — с умножением многочленов на элементы поля.
Множество векторов, которое не является линейно зависимым, называется линейно независимым. Никакой вектор из множества линейно независимых векторов не может быть представлен в виде линейной комбинации остальных векторов этого множества. Отметим, что нулевой вектор 0 не может принадлежать линейно независимому множеству; каждое множество, содержащее 0, является линейно зависимым.
О множестве векторов говорят, что оно порождает векторное пространство, если каждый вектор пространства равен хотя бы одной линейной комбинации векторов из этого множества. Векторное пространство, порождаемое конечным множеством векторов, называется конечномерным векторным пространством. Мы в первую очередь интересуемся конечномерными векторными пространствами.
Два множества линейно независимых векторов, порождающие одно и то же векторное пространство, содержат одинаковое количество векторов.
Широко используемые разделы прикладной математики — линейная алгебра, в частности теория матриц.
Определение.(п X т)-матрицей А над кольцом R называется прямоугольная таблица, состоящая из п строк и т столбцов и содержащая пт элементов из кольца R:

В большинстве приложений кольцо R в действительности является полем, и мы ограничимся этим случаем. Как правило, мы будем рассматривать матрицы над конечным полем GF (q).
Множество элементов aij для которых номер строки совпадает с номером столбца, называется главной диагональю. Если п равно т, то матрица называется квадратной матрицей, (n X п)-матрица, "все элементы главной диагонали которой равны единичному элементу поля, а остальные элементы равны нулевому элементу поля, называется единичной (п X п)-матрицей.
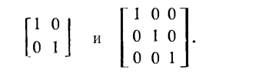
Две матрицы (п X m) A и B над полем GF (q) можно складывать по правилу
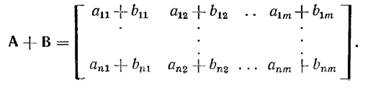
Матрицу А(п X m) можно умножать на элемент поля β по правилу
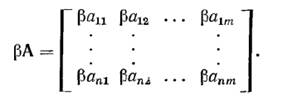
Матрицу А(l X m) можно умножать на матрицу B(n X m) получив результирующую матрицу С(l X m) по правилу
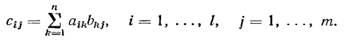
Строки (n X т)-матрицы А над GF (q) можно рассматривать как множество m-мерных векторов над GF (q). Пространство строк матрицы А определяется как множество всех линейных комбинаций векторов-строк матрицы А. Размерность пространства строк называется рангом матрицы по строкам. Аналогично столбцы матрицы А можно рассматривать как множество «-мерных векторов над GF (q). Пространство столбцов матрицы А определяется как множество всех линейных комбинаций векторов-столбцов матрицы А, а размерность пространства столбцов называется рангом матрицы по столбцам. Множество всех векторов V, таких, что AV = О, называется нулевым пространством матрицы А. Ясно, что нулевое пространство является подпространством в GF" (q)- В частности, нулевое пространство является ортогональным дополнением пространства строк матрицы А, так как нулевое пространство можно задать как множество всех векторов, ортогональных ко всем векторам пространства строк.
Элементарными операциями над строками матрицы называются следующие действия:
1) перестановка двух произвольных строк;
2) умножение произвольной строки на нулевой элемент поля;
3) замена произвольной строки па сумму ее самой и некоторого кратного любой другой строки.
Каждая элементарная операция над строками обратима, и обратная операция имеет такой же вид. Каждая элементарная операция над строками (n X n)-матрицы А может быть выполнена путем левого умножения А на соответствующим образом подобранную так называемую элементарную (n X n)-матрицу F.
Глава 2. Структура линейных блоковых кодов.
Напомним, что векторное пространство GF (q) представляет собой множество л-последовательностей элементов из GF (q) с покомпонентным сложением и умножением на скаляр. Наиболее важным частным случаем является GF (2) — векторное пространство двоичных слов длины n, в котором при сложении двух векторов в каждой компоненте происходит сложение по модулю 2.
Определение 3.I.I. Линейный код есть подпространство в GF (q)
Таким образом, линейный множество n-последовательностей над GF(q) называемых кодовыми словами, такое, что сумма двух кодовых слов является кодовым словом, и произведение любого кодового слова на элемент ноля также является кодовым словом. В любом линейном коде нулевое слово как начало координат векторного пространства всегда есть кодовое слово. Точнее, если с — кодовое слово, то — с также кодовое слово и, следовательно, с (— с) тоже будет кодовым словом.
Каждое слово в линейном коде связано с остальными словами кода так же, как любое другое кодовое слово. Расположение соседних кодовых слов вокруг нулевого слова есть типичное расположение слов вокруг любого другого кодового слова. Например, предположим, что с — некоторое кодовое слово и с1..., сr —• кодовые слова, находящиеся на некотором расстоянии d от с; тогда с - с—нулевое слово и с, —с, с2 — с,..., сr,. —
— с—кодовые слова, находящиеся на расстоянии d от нулевого слова. Таким образом, для определения минимального расстояния линейного кода достаточно определить расстояние между нулевым словом и ближайшим к нему другим кодовым словом.
Глава 3.Матричное описание линейных блоковых кодов.
Линейный код b образует подпространство в GFn (q). Для изучения этих кодов будет полезна теория линейных пространств. Любое множество базисных векторов может быть использовано в качестве строк для построения (kХn)-матрицы G, которая называется порождающей матрицей кода. Пространство строк матрицы G есть линейный код b, любое кодовое слово есть линейная комбинация строк из G. Множество qk кодовых слов называется линейным (n, k)-кодом.
Любое взаимно однозначное соответствие k-последовательностей действий и кодовых слов может быть использовано для кодирования, но наиболее естественный способ кодирования использует отображение
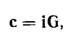
i-информационное слово, представляющее собой k-последовательность кодируемых информационных символов, а c-образующая кодовое n-последовательность. Задаваемое последним равенством соответствие меджу информационным и кодовым словами определяет кодер и зависит от выбора базисных векторов в качестве строк матрицы G; в то же время само множество кодовых слов не зависит от этого выбора.
В качестве примера двоичного блокового кода рассмотрим пораждающую матрицу

В этом случае информационное слово
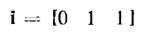
Будет кодироваться в кодовое слово
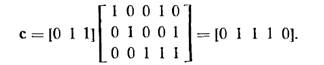
Порождающая матрица будет являться сжатым описанием линейного кода.
Ортогональное дополнение b’ имеет размерность n-k, и любой его базис также состоит из n-k векторов. Пусть H-матрица со строками, являющимися этими базисными векторами. Тогда n-последовательность c является кодовым словом в том и только том случае, когда она ортогональна каждой вектор-строке матрицы H
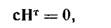
Для порождающей матрицы

Каждая порождающая матрица G эквивалентна некоторой матрице канонического ступенчатого вида, и поскольку строки линейно независимы, все строки эквивалентной матрицы являются ненулевыми. Эквивалентную матрицу можно записать
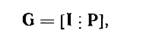
Где P есть n X (n-k)-матрица. Любая порождающая матрица может быть приведена к такому частному виду при помощи последовательности элементарных операций над строками и последующей перестановки столбцов. Такую порождающую матрицу будем называть порождающей матрицей в систематическом виде.
Систематическим кодом называется код, которого каждое слово начинается с информационных символов.
Систематический линейный код кодируется умножением информационного вектора на порождающую матрицу G в систематическом виде, а каждая порождающая матрица G эквивалентна некоторой систематической матрице

Тогда i=[0 1 1] при систематическом кодировании отобразится в слово c=[0 1 1 1 0].
1. Перечислением кодовых слов, т.е. составлении списка всех кодовых слов кода.
Пример. В таблице 1 представлены все кодовые слова (5,3) - кода (ai - информационные, а bi - проверочные символы).
| Таблица 1 | |||||
№ 
| a1 | a2 | a3 | b1 | b2 |
2. Системой проверочных уравнений, определяющих правила формирования проверочных символов по известным информационным:

где
j - номер проверочного символа;
i - номер информационного символа;
hij - коэффициенты, принимающие значения 0 или 1 в соответствии с правилами формирования конкретных групповых кодов.
Пример. Для кода (5,3) проверочные уравнения имеют вид:
b1= a2 + a3;
b2= a1 + a2.
Матричное, основанное на построении порождающей и проверочной матриц.
Векторное пространство Vn над GF(2) включает в себя 2n векторов (n-последовательностей), а подпространством его является множество из 2k кодовых слов длины n, которое однозначно определяется его базисом, состоящим из k линейно независимых векторов. Поэтому линейный (n,k) - код полностью определяется набором из k кодовых слов, принадлежащих этому коду. Набор из k кодовых слов, соответствующих базису, обычно представляется в виде матрицы, которая называется порождающей.
Пример. (5,3) - код, который был представлен в таблице 1, может быть задан матрицей
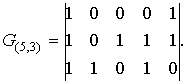
Остальные кодовые слова получаются сложением строк матриц в различных сочетаниях.
Общее количество различных вариантов порождающих матрицу определяется выражением
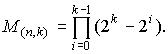
Для исключения неоднозначности в записи G(n,k) вводят понятие о канонической или систематической форме матрицы, которая имеет вид
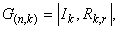
где
Ik - единичная матрица, содержащая информационные символы;
Rk,r - прямоугольная матрица, составленная из проверочных символов.
Пример. Порождающая матрица в систематическом виде для (5,3) - кода
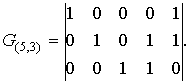
Порождающая матрица G(n,k) в систематическом виде может быть получена из любой другой матрицы посредством элементарных операций над строками (перестановкой двух произвольных строк, заменой произвольной строки на сумму ее самой и ряда других) и дальнейшей перестановкой столбцов.
Проверочная матрица в систематическом виде имеет вид
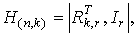
где Ir - единичная матрица; 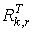 - прямоугольная матрица в транспонированном виде матрицы Rk,r из порождающей матрицы.
- прямоугольная матрица в транспонированном виде матрицы Rk,r из порождающей матрицы.
Пример. Проверочная матрица (5,3) - кода
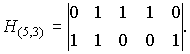
Глава 4. Стандартное расположение.
Поскольку разность двух кодовых слов линейного кода является кодовым словом, пулевое слово всегда будет кодовым. Если мы знаем, какое множество принятых слов линейного кода лежит ближе всего к нулевому слову, то с помощью простого сдвига начала координат нетрудно выяснить, какие из принятых слов лежат ближе всего к любому другому кодовому слову.
Пусть d* нечетно и d* — 2i + 1. Внутри сферы радиуса t с центром в нулевом слове находится множество точек S={v|d(0, V)<t}-Эта сфера содержит все принятые слова, которые декодируются в нулевое кодовое слово. Внутри сферы радиуса t с центром в кодовом слове с находится множество точек
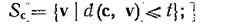
тогда

Таким образом, мы можем выписать точки, лежащие внутри каждой сферы декодирования или (что эффективнее) внутри сферы декодирования с центром в нулевом слове, а точки, лежащие внутри других сфер получать но мере необходимости с помощью простого сдвига.
Стандартное расположение представляет собой способ описания всех этих сфер. Пусть 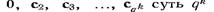 кодовых слов (n, k)-кода.. В первой строке выпишем все кодовые слова. Из оставшихся в GFn (q) слов, лежащих на расстоянии 1 от нулевого слова, выберем любое и обозначим его v,. Во второй строке
кодовых слов (n, k)-кода.. В первой строке выпишем все кодовые слова. Из оставшихся в GFn (q) слов, лежащих на расстоянии 1 от нулевого слова, выберем любое и обозначим его v,. Во второй строке 
запишем 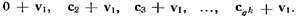 . Таким же, образом строятся следующие строки. На j-м шаге выберем слово
. Таким же, образом строятся следующие строки. На j-м шаге выберем слово 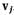 , которое является ближайшим к нулевому и отсутствует в предыдущих строках, и запишем в j-й строке
, которое является ближайшим к нулевому и отсутствует в предыдущих строках, и запишем в j-й строке 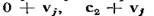 . Эта процедура закончится, когда после очередного шага не останется неиспользованных слов.
. Эта процедура закончится, когда после очередного шага не останется неиспользованных слов.
Вывод
Таким образом, линейные коды образуют векторное пространство и обладают следующим важными свойствами: два кодовых слова можно сложить, используя подходящее определение суммы, и получить третье кодовое слово. Второе свойство состоит в том, что линейность существенно упрощает задачу вычисления параметров кода, поскольку расстояние между двумя кодовыми словами при этом эквивалентно расстоянию между кодовым словом, состоящим целиком из нулей, и некоторым другим кодовым словом.
Список Литературы
Мышев А.В- «Основы прикладной теории кодирования информации»
Питерсон, Уелдон.- «Коды исправляющие ошибки»
В.В. Лидовский – «Теория Информации»