Для нахождения интегралов данного типа используется метод интегрирования «по частям». Напомним, что формула интегрирования по частям имеет вид:  . Основные приемы, связанные с интегрированием «по частям» приведены в таблице 3.
. Основные приемы, связанные с интегрированием «по частям» приведены в таблице 3.
Решение задачи 6
Данный интеграл имеет вид  , где
, где  . Такие интегралы берутся «по частям». За функцию
. Такие интегралы берутся «по частям». За функцию  принимается
принимается  и применяется
и применяется  раз формула интегрирования по частям. В нашем случае
раз формула интегрирования по частям. В нашем случае  , поэтому формулу интегрирования «по частям» здесь достаточно использовать только один раз.
, поэтому формулу интегрирования «по частям» здесь достаточно использовать только один раз.

 .
.
Задача 7
Вычислить интеграл  .
.
Решение задачи 7
Данный интеграл относится к виду  . Такие интегралы берутся «по частям». За функцию
. Такие интегралы берутся «по частям». За функцию  принимается
принимается  и применяется
и применяется  раз формула интегрирования по частям. В нашем случае
раз формула интегрирования по частям. В нашем случае  , формулу интегрирования «по частям» здесь достаточно использовать два раза.
, формулу интегрирования «по частям» здесь достаточно использовать два раза.

 .
.
Применим ко второму интегралу еще раз формулу интегрирования по частям.
 .
.
Вычислим интеграл  отдельно, сделав предварительно некоторые алгебраические преобразования. Сначала добавим и вычтем 1 в числителе, а затем разобьем исходный интеграл на два табличных интеграла.
отдельно, сделав предварительно некоторые алгебраические преобразования. Сначала добавим и вычтем 1 в числителе, а затем разобьем исходный интеграл на два табличных интеграла.

 .
.
Отсюда

Применив метод подведения под знак дифференциала последние два интеграла, можно вычислить

Окончательный ответ


 .
.
Задача 8
Вычислить интеграл  .
.
Справочный материал
В данном интеграле подынтегральная функция является дробно-рациональной функцией, то есть представляет собой рациональную дробь вида
 .
.
Метод интегрирования рациональных дробей сводится к разложению подынтегральной функции на сумму элементарных дробей, интегралы от которых являются табличными интегралами.
Если знаменатель дроби можно разложить на множители
 где
где  и
и 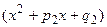 не имеют вещественных корней, то правильная дробь
не имеют вещественных корней, то правильная дробь 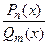 , где
, где  , может быть представлена в виде суммы элементарных дробей:
, может быть представлена в виде суммы элементарных дробей:


Приведем примеры элементарных или простейших дробей.
1.  ,
,
2.  , (
, ( - целое положительное число)
- целое положительное число)
3.  (дискриминант
(дискриминант  ),
),
4.  (
( и
и  - целое положительное число).
- целое положительное число).
Интегралы от этих дробей имеют вид:
1.  .
.
2.  .
.
3. 
 .
.
4.  .
.
Интегрирование простейших дробей этого типа требует более сложных вычислений. Мы не будем здесь подробно рассматривать вычисления, связанные с интегрированием дробей данного типа, так как эти вычисления приведены в компендиуме по данной теме. Приведем окончательную формулу.

Вычисление последнего интеграла сводятся к рекуррентным соотношениям вида
 .
.
Если дробь неправильная, предварительно следует выделить целую часть этой дроби. Неправильную рациональную дробь всегда можно представить в виде суммы рационального выражения (многочлена) и правильной рациональной дроби, то есть рациональная дробь  при
при  представима в виде:
представима в виде:
 , где
, где  .
.
Такое представление неправильной рациональной дроби и называется выделением целой части.
Решение задачи 8
В нашем примере степень числителя и знаменателя одинакова и равна 3. Следовательно, предварительно необходимо выделить целую часть рациональной дроби. Рассмотрим подынтегральную функцию:

Выделение полной части рациональной дроби можно осуществить путем деления многочленов.


| 
|
–

| |

|
Таким образом
 .
.
Полученную неправильную рациональную дробь разложим на простейшие дроби. Знаменатель можно представить в виде  . Следовательно, дробь представима в виде
. Следовательно, дробь представима в виде
 .
.
Приведем выражение, стоящее в правой части равенства к общему знаменателю

Отсюда получим тождество
 .
.
Коэффициенты  можно найти двумя способами.
можно найти двумя способами.
1 способ. Приравнивая коэффициенты при одинаковых степенях в обеих частях тождества.
Коэффициенты при одинаковых степенях  в обеих частях тождества должны быть равны:
в обеих частях тождества должны быть равны:

| = | 
| |

| –2 | = | 
|

| –8 | = | 
|
Таким образом, для нахождения коэффициентов получена система линейных алгебраических уравнений, решив которую найдем неизвестные коэффициенты.
 .
.
Отсюда  ,
,  ,
,  .
.
2 способ. Придавая переменной  конкретные значения.
конкретные значения.
Подставим значение  в полученное тождество
в полученное тождество
 ,
,
определим  .
.
Подставив значение  определим
определим  , и, наконец, подставив
, и, наконец, подставив  , определим
, определим  .
.
Теперь исходный интеграл запишется в виде:

 .
.
Полученный интеграл можно записать в более компактном виде, используя свойства логарифма.
 .
.
Задача 9
Вычислить интеграл  .
.
Справочный материал
В данном интеграле подынтегральная функция так же является дробно-рациональной функцией, и представляет собой правильную рациональную дробь, в отличие от примера, рассмотренного в предыдущем пункте. Метод решения – разложение подынтегральной функции на простейшие рациональные дроби. Этот метод был изложен в предыдущем пункте.
Решение задачи 9
Знаменатель можно представить в виде  . Следовательно, дробь представима в виде
. Следовательно, дробь представима в виде
 .
.
Приведем выражение, стоящее в правой части равенства к общему знаменателю

Отсюда получим тождество
 .
.
Коэффициенты при одинаковых степенях  в обеих частях тождества должны быть равны:
в обеих частях тождества должны быть равны:

| = | 
| |

| = | 
| |

| -3 | = | 
|
Таким образом, для нахождения коэффициентов получена система линейных алгебраических уравнений, решив которую найдем неизвестные коэффициенты.
 .
.
Выразим коэффициенты  и
и  через
через  и подставим их во второе уравнение
и подставим их во второе уравнение
 или
или  ,
,  ,
,  .
.
Теперь исходный интеграл запишется в виде:
 Первый из интегралов является табличным, формула (2).
Первый из интегралов является табличным, формула (2).
Второй интеграл можно вычислить двумя способами.
1 способ. Второй интеграл представляет собой интеграл типа 3 (см. справочный материал к задаче 8), поэтому можно применить формулу.

 .
.
В нашем случае
 ,
,  .
.
 .
.
 .
.
2 способ. Выделение полного квадрата в знаменателе подынтегрального выражения.
Представим  в виде полного квадрата.
в виде полного квадрата.
 .
.
Тогда интеграл можно переписать в виде:

Рассмотрим первый из интегралов

Второй из интегралов – табличный, формула (12).
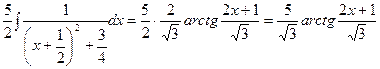 .
.
Таким образом,
 .
.
Окончательный ответ  .
.
Задача 10
Вычислить интеграл  .
.
Справочный материал
В данном примере подынтегральная функция содержит иррациональное выражение. Метод решения здесь: применение подходящей замены. Обычно замену выбирают так, чтобы избавиться от иррационального выражения.
Решение задачи 10
Введем новую переменную  . Отсюда
. Отсюда 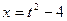 ,
,  . Подставим полученные выражения в интеграл
. Подставим полученные выражения в интеграл

Вернемся к исходной переменной

Задача 11
 .
.
Справочный материал
В данном примере подынтегральная функция имеет вид  , где
, где 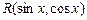 ― рациональная функция от
― рациональная функция от  и
и  . Метод решения здесь основан на применении так называемой универсальной подстановки
. Метод решения здесь основан на применении так называемой универсальной подстановки
 , или
, или  .
.
Тогда
 ,
, 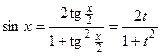 ,
,  .
.
Таким образом, данная подстановка, приводит исходный интеграл от тригонометрических функций  и
и  к интегралу от рациональной функции новой переменной
к интегралу от рациональной функции новой переменной  .
.
 .
.
Решение задачи 11
Применив универсальную подстановку, получим

 .
.
Таким образом, интеграл от тригонометрических функций свелся к интегралу от рациональной дроби.
Разложим подинтегральную функцию на простейшие дроби
 .
.
Отсюда
 .
.
Подставим в ту формулу  , получим
, получим  , подставим в ту формулу
, подставим в ту формулу  , получим
, получим  . Таким образом,
. Таким образом,
 .
.
Возвращаясь к исходной переменной, получим:

 .
.
Задача 12
Вычислить интеграл 
Справочный материал
В данном примере требуется найти значение определенного интеграла. Для вычисления определенных интегралов используется формула Ньютона-Лейбница
 ,
,
где  есть какая-либо первообразная для функции
есть какая-либо первообразная для функции  .
.
Подынтегральная функция имеет вид  , где
, где 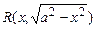 ― рациональная функция своих аргументов. Метод решения здесь основан на применении подстановки
― рациональная функция своих аргументов. Метод решения здесь основан на применении подстановки  . Тогда
. Тогда  .
.
Решение задачи 12
1 способ. Рассмотрим сначала неопределенный интеграл. Применив подстановку  ,
,
тогда 
получим

Представим в знаменателе число  в виде
в виде 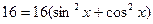 , и вынесем
, и вынесем  за скобку, получим
за скобку, получим

 .
.
Возвратимся к исходной переменной. Найдем сначала
 .
.
Получим:
 .
.
2 способ. Можно интегрировать непосредственно определенный интеграл. В этом случае нужно пересчитать пределы интегрирования. При  , имеем
, имеем  , отсюда
, отсюда  . При
. При  , имеем
, имеем  , отсюда
, отсюда  .
.

 .
.
Задача 13
Вычислить площадь фигуры, ограниченной линиями:  ,
,  .
.
Справочный материал
Определенный интеграл используется для нахождения площадей плоских фигур. Площадь криволинейной трапеции, ограниченной кривыми  ,
,  и прямыми
и прямыми  ,
,  (рис.1), равна
(рис.1), равна
.  .
.
 |




Рис.1 Площадь криволинейной трапеции
Решение задачи 13
В данном случае фигура ограничена двумя линиями – прямой и параболой.

Рис. 2.
Для определения пределов интегрирования найдем точки пресечения этих кривых. Они находятся как решения уравнения 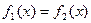 .
.
Для определения пределов интегрирования найдем точки пресечения этих кривых. Они находятся как решения уравнения 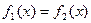 . В нашем случае
. В нашем случае  ,
,  . Для определения точек пересечения имеем уравнение:
. Для определения точек пересечения имеем уравнение:
 , или
, или  . Решая уравнение, находим
. Решая уравнение, находим  . Следовательно,
. Следовательно,  .
.
Осталось вычислить определенный интеграл

Задача 14
Вычислить площадь фигуры, ограниченной линией:
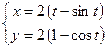 , при
, при  .
.
Справочный материал
Для определения площади фигуры, ограниченной кривой, заданной в параметрическом виде
 ,
,
и прямыми вида  и
и  , используется формула:
, используется формула:
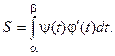
где  . Пределы интегрирования
. Пределы интегрирования  и
и  находятся из уравнений
находятся из уравнений  .
.
Решение задачи 14
Данная кривая является циклоидой.

Рис. 3
В нашем случае
 .
.
Пределы интегрирования  и
и  находятся из уравнений
находятся из уравнений  , то есть из равнений
, то есть из равнений 
 . Решая их находим
. Решая их находим  ,
,  , поэтому искомая площадь равна значению определенного интеграла
, поэтому искомая площадь равна значению определенного интеграла


Задача 15
Вычислить длину дуги кривой
 , при
, при  .
.
Справочный материал
Для определения длины дуги кривой, заданной в параметрическом виде 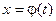 и
и  , где
, где  используется формула:
используется формула:
 .
.
Решение задачи 15
Заданная кривая является астроидой

Рис. 4.

 .
.
| 1 вариант | |
1.  .
2. .
2.  .
3. .
3.  .
4. .
4.  .
5. .
5.  .
6. .
6.  .
7. .
7.  . .
|
8.  .
9. .
9.  .
10. .
10.  .
11. .
11.  .
12. .
12.  . .
|
13.Вычислить площадь фигуры, ограниченной линиями:
 , ,  .
14.Вычислить площадь фигуры, ограниченной линиями: .
14.Вычислить площадь фигуры, ограниченной линиями:
 , ,  , при , при  .
15.Найти объем тела, полученного от вращения фигуры, ограниченной линиями .
15.Найти объем тела, полученного от вращения фигуры, ограниченной линиями  , при , при  , вокруг оси , вокруг оси 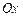 . .
| |
| 2 вариант | |
1.  . 15. Найти длину дуги кривой
2. . 15. Найти длину дуги кривой
2.  .
3. .
3.  .
4. .
4.  .
5. .
5.  .
6. .
6.  . .
|
7.  .
8. .
8.  .
9. .
9.  .
10. .
10.  .
11. .
11.  .
12. .
12. 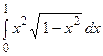 . .
|
13.Вычислить площадь фигуры, ограниченной линиями:  и и  .
14.Вычислить площадь фигуры, ограниченной линиями: .
14.Вычислить площадь фигуры, ограниченной линиями:
 , ,  , при , при  .
15.Вычислить длину дуги кривой .
15.Вычислить длину дуги кривой  от ее вершины до точки от ее вершины до точки  . .
| |
| 3 вариант. | |
1. 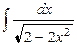 .
2. .
2.  .
3. .
3.  .
4. .
4.  .
5. .
5.  .
6. .
6.  .
7. .
7.  . .
|
8.  .
9. .
9.  .
10. .
10.  .
11. .
11.  .
12. .
12.  . .
|
13.Вычислить площадь фигуры, ограниченной линиями:
 , ,  , ,  .
14.Вычислить площадь фигуры, ограниченной линиями: .
14.Вычислить площадь фигуры, ограниченной линиями:
 и и  , при , при  и и  .
15.Найти объем тела, образованного вращением фигуры, ограниченной линиями .
15.Найти объем тела, образованного вращением фигуры, ограниченной линиями  и и  , вокруг оси , вокруг оси 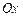 . .
|
| 4 вариант. | |
1.  .
2. .
2.  .
3. .
3.  .
4. .
4.  .
5. .
5.  .
6. .
6.  .
7. .
7.  . .
|
8. 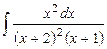 .
9. .
9.  .
10. .
10.  .
11. .
11.  .
12. .
12.  . .
|
13.Вычислить площадь фигуры, ограниченной линиями:
 , ,  , ,  , ,  .
14.Вычислить площадь фигуры, ограниченной линиями: .
14.Вычислить площадь фигуры, ограниченной линиями:
 , ,  , при , при  .
15.Вычислить длину дуги линии .
15.Вычислить длину дуги линии  , при , при  . .
|
| 5 вариант. | |
1.  .
2. .
2.  .
3. .
3.  .
4. .
4.  .
5. .
5.  .
6. .
6.  .
7. .
7.  . .
|
8.  .
9. .
9.  .
10. .
10.  .
11. .
11.  .
12. .
12.  . .
|
13.Вычислить площадь фигуры, ограниченной линиями:
 , , 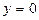 , при , при  .
14.Вычислить площадь фигуры, ограниченной линиями: .
14.Вычислить площадь фигуры, ограниченной линиями:  , ,  , при , при  .
15.Вычислить объем тела, образованного вращением вокруг оси .
15.Вычислить объем тела, образованного вращением вокруг оси  фигуры, ограниченной линией: фигуры, ограниченной линией:  . .
|
| 6 вариант. | |
1.  .
2. .
2.  .
3. .
3.  .
4. .
4.  .
5. .
5.  .
6. .
6.  . .
|
7.  .
8. .
8.  .
9. .
9.  .
10. .
10.  .
11. .
11.  .
12. .
12.  . .
|
13.Вычислить площадь фигуры, ограниченной линиями
 , ,  , при , при  .
14.Вычислить площадь фигуры, ограниченной линиями: .
14.Вычислить площадь фигуры, ограниченной линиями:
 , ,  ,при ,при .
15.Вычислить длину дуги кривой .
15.Вычислить длину дуги кривой
 ,при ,при . .
|
| 7 вариант. | |
1.  .
2. .
2.  .
3. .
3. 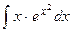 .
4. .
4.  .
5. .
5.  .
6. .
6.  .
7. .
7.  . .
| 8.  .
9. .
9.  .
10. .
10.  .
11. .
11.  .
12. .
12.  . .
|
13.Вычислить площадь фигуры, ограниченной линиями:
 , ,  , ,  .
14.Вычислить площадь фигуры, ограниченной линией: .
14.Вычислить площадь фигуры, ограниченной линией:
 .
15.Найти объем тела, образованного вращением вокруг оси .
15.Найти объем тела, образованного вращением вокруг оси  фигуры, ограниченной линиями: фигуры, ограниченной линиями:
 . .  , ,  , ,
|
| 8 вариант. | |
1.  .
2. .
2.  .
3. .
3.  .
4. .
4.  .
5. .
5.  .
6. .
6. 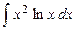 .
7. .
7.  . .
|
8.  .
9. .
9.  .
10. .
10.  .
11. .
11.  .
12. .
12.  . .
|
13.Вычислить площадь фигуры, ограниченной линиями:
 , ,  , ,  , ,  .
14.Вычислить площадь фигуры, ограниченной линиями: .
14.Вычислить площадь фигуры, ограниченной линиями:
 , ,  ,при ,при  и и  .
15.Вычислить длину дуги кривой .
15.Вычислить длину дуги кривой  ,при ,при . .
|
| 9 вариант. | ||
1.  .
2. .
2.  .
3. .
3.  .
4. .
4.  .
5. .
5.  .
6. .
6.  . .
| 7.  .
8. .
8.  .
9. .
9.  .
10. .
10. 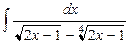 .
11. .
11.  .
12. .
12.  . .
| |
13.Вычислить площадь фигуры, ограниченной линиями:
 , , 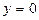 ,при ,при  .
14.Вычислить плошадь фигуры, ограниченной линиями: .
14.Вычислить плошадь фигуры, ограниченной линиями:
 , ,  ,при ,при  .
15.Вычислить объем тела, образованного вращением фигуры, ограниченной линиями: .
15.Вычислить объем тела, образованного вращением фигуры, ограниченной линиями:  и и  , вокруг , вокруг  . .
| ||
| 10 вариант. | ||
1.  .
2. .
2.  .
3. .
3.  .
4. .
4.  .
5. .
5.  .
6. .
6.  .
7. .
7.  . .
| 8.  .
9. .
9.  .
10. .
10.  .
11. .
11.  .
12. .
12.  . .
| |
13.Вычислить площадь фигуры, ограниченной линиями:
 , ,  , , 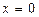 .
14.Вычислить площадь фигуры, ограниченной линиями: .
14.Вычислить площадь фигуры, ограниченной линиями:
 , ,  ,при ,при  .
15.Найти длину дуги кривой .
15.Найти длину дуги кривой  ,при ,при  . .
| ||
| 11 Вариант. | ||||
1.  .
2. .
2.  .
3. .
3.  .
4. .
4.  .
5. .
5.  .
6. .
6.  . .
| 7.  /
8. /
8.
Поиск по сайту©2015-2025 poisk-ru.ru
Все права принадлежать их авторам. Данный сайт не претендует на авторства, а предоставляет бесплатное использование. Дата создания страницы: 2020-05-09 Нарушение авторских прав и Нарушение персональных данных |
Поиск по сайту: Читайте также: Деталирование сборочного чертежа Когда производственнику особенно важно наличие гибких производственных мощностей? Собственные движения и пространственные скорости звезд |