РАБОЧАЯ ТЕТРАДЬ
Санкт-Петербург
Справочный материал
Задания данного типового расчета делятся на три типа: нахождение неопределенных интегралов, вычисление определенных интегралов и применение интегралов к решению геометрических задач.
Перечислим основные методы нахождения неопределенного интеграла.
Метод 1. Непосредственное интегрирование. В этом случае необходимо с помощью элементарных преобразований привести интеграл к табличному виду. Ниже приводятся первообразные для основных элементарных функций. При решении задач мы будем ссылаться на эту таблицу, указывая соответствующий номер формулы.
Таблица 1.
 , где , где 
| (1) |

| (2) |

| (3) |

| (4) |

| (5) |

| (6) |

| (7) |

| (8) |

| (9) |

| (10) |

| (11) |

| (12) |

| (13) |
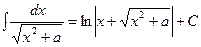
| (14) |

| (15) |

| (16) |

| (17) |

| (18) |

| (19) |

| (20) |
Метод 2. Замена переменной или интегрирование подстановкой. Методы, использующие замену переменной можно разделить на две группы:
Подведение под знак дифференциала.
Интегрирование посредством замены переменной.
Подведение под знак дифференциала используется, если подинтегральная функция представима в виде
 .
.
Используя определение дифференциала  , исходный интеграл перепишется в виде
, исходный интеграл перепишется в виде
 ,
,
где интеграл  является табличным интегралом.
является табличным интегралом.
Например,  . Здесь использована формула
. Здесь использована формула  .
.
Приведем преобразования дифференциалов, используемых наиболее часто:
Таблица 2.
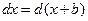 , где , где 
| (21) |
 , где , где 
| (22) |

| (23) |

| (24) |

| (25) |

| (26) |
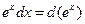
| (27) |
Интегрирование посредством замены переменной. Для нахождения интеграла можно заменить переменную  новой переменной
новой переменной  , связанной с
, связанной с  подходящей формулой
подходящей формулой  . Определив для этой формулы
. Определив для этой формулы  и подставляя в интеграл, получим
и подставляя в интеграл, получим
 .
.
Если полученный интеграл с новой переменной будет найден, то преобразовав результат к переменной  , получим искомое выражение заданного интеграла.
, получим искомое выражение заданного интеграла.
Иногда замену переменной удобнее сделать в виде  . Определив для этой формулы
. Определив для этой формулы  , получим
, получим  . Подставив
. Подставив  и
и  в исходный интеграл, получим интеграл от новой переменной.
в исходный интеграл, получим интеграл от новой переменной.
Метод 3. Интегрирование по частям. Ф ормула интегрирования по частям имеет вид:
 .
.
Этот метод используется чаще всего для интегралов специального вида  , где
, где  многочлен степени
многочлен степени  , а
, а  такая функция, что интеграл
такая функция, что интеграл 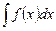 является табличным или легко сводится к такому. В таблице 3 приведены основные типы интегралов, для которых используется этот метод.
является табличным или легко сводится к такому. В таблице 3 приведены основные типы интегралов, для которых используется этот метод.
Таблица 3.
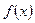
| 
| 
|
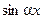
| 
| 
|
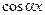
| 
| 
|

| 
| 
|

| 
| 
|
 , где , где 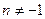
| 
| 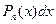
|

| 
| 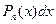
|

| 
| 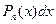
|
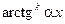
| 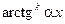
| 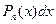
|

| 
| 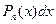
|
Задача 1.1
Вычислить интеграл  .
.
Справочный материал
Для нахождения интегралов данного типа необходимо с помощью элементарных преобразований привести интеграл к табличному виду.
Решение задачи 1.1
 .
.
По свойству интеграла (см. компендиум по этой теме), постоянный множитель можно вынести за знак интеграла. Полученный интеграл является табличным и его можно вычислить по формуле (10).
 .
.
Задача 1.2
Вычислить интеграл  .
.
Решение задачи 1.2
Используя свойство дифференциала (см. компендиум по этой теме), имеем  . Тогда исходный интеграл можно записать в виде
. Тогда исходный интеграл можно записать в виде
 .
.
Полученный интеграл является табличным, см. формулу (1).
 .
.
Задача 2
Вычислить интеграл  .
.
Справочный материал
Для нахождения интегралов данного типа используется метод подведения под знак дифференциала. Все необходимые формулы приведены в таблице 2.
Решение задачи 2
Используя свойство дифференциала  , исходный интеграл можно записать в виде
, исходный интеграл можно записать в виде
 .
.
Введем обозначение  , тогда интеграл запишется в виде
, тогда интеграл запишется в виде  . Полученный интеграл является табличным интегралом, его можно вычислить по формуле (1).
. Полученный интеграл является табличным интегралом, его можно вычислить по формуле (1).
 .
.
Задача 3
Вычислить интеграл  .
.
Справочный материал для задач 3, 4, 5
Задачи этого типа похожи на задачу 2, рассмотренную в предыдущем пункте, но они более сложные. Для нахождения интегралов здесь также используется метод подведения под знак дифференциала. Иногда требуется предварительно произвести некоторые алгебраические преобразования исходного интеграла.
Решение задачи 3
По свойству дифференциала  , тогда исходный интеграл можно записать в виде
, тогда исходный интеграл можно записать в виде
 .
.
Полученный интеграл является табличным интегралом, его можно вычислить по формуле (11).
 .
.
Задача 4
Вычислить интеграл  .
.
Решение задачи 4
Используя свойство дифференциала  , исходный интеграл можно записать в виде
, исходный интеграл можно записать в виде
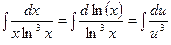 .
.
Полученный интеграл является табличным интегралом, формула (1).
 .
.
Задача 5.1
Вычислить интеграл  .
.
Решение задачи 5.1
Выполним предварительно алгебраические преобразования подынтегральной функции
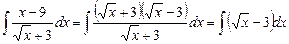 .
.
Используя свойства интеграла его можно записать в виде
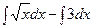 .
.
Каждый из полученных интегралов является табличным.
 .
.
Задача 5.2
Вычислить интеграл 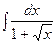 .
.
Справочный материал
Для решения задач такого типа требуется замена переменной.
Решение задачи 5.2
Для вычисления интеграла используем метод – интегрирование посредством замены переменной. Положим  , тогда
, тогда  . Подставим в интеграл
. Подставим в интеграл

Возвращаясь к исходной переменной, получим
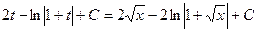 .
.
Задача 6
Вычислить интеграл  .
.