Критерии предельных напряженно-деформированных состояний изотропных материалов

Значительные объемы теоретических исследований и экспериментальных обоснований предельных состоянии материалов и конструкций, базирующиеся на анализе напряженно-деформированных состояний и характеристиках механических свойств (пределы текучести, прочности, разрушающая деформация и т.д.), привели к тому, что и механике деформируемого твердого тела оформилась как самостоятельное направление теория предельных состояний. Обзор работ по различным аспектам проблемы содержится в [33-39].

Согласно традиционным трактовкам, предельное (опасное) напряженно-деформированное состояние материала возникает, когда некоторая функция главных напряжений 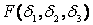достигнет своего предельного значения:

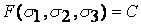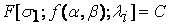или (3.1)

где 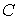— критерий предельного состояния (минимальное значение параметра, характеризующего момент наступления предельного состояния); 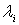— параметры материала.

Уравнение (3.1) включает в себя функцию 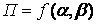, описывающую вид напряженного состояния (линейное, плоское напряженное состояние, плоская деформация, объемное) Параметры этой функции характеризуют жесткость напряженного состояния 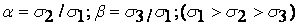, изменяясь в диапазоне .

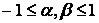В зависимости от условий деформирования (температура, скорость нагружения, среда и т.д.) один и тот же материал может находиться в различных механических состояниях: упругом, упруго-пластическом, пластическом и в состоянии разрушения. Для конструкционных материалов характерна следующая последовательность смены состояний при деформировании:

 упругая стадия;

 пластическая стадия (накопление повреждений, разрыхление материала, пластическое течение);

 образование и накопление микротрещин, формирование и развитие магистральной трещины до разрушения.

Переход материала от упругой стадии деформирования к пластической описывается критериями пластичности, а переход материала от стадии упругого или пластического деформирования к стадии разрушения описывается критериями разрушения. Таким образом, в зависимости от механического состояния материала уравне­ние (3.1) может характеризовать:

 начало пластического течения, тогда 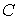— критерий пластич­ности (текучести):

 момент разрушения, тогда 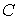— критерий разрушения.

Если выполняется условие

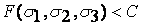(3.2)

то материал согласно критерию пластичности не переходит в пла­стическое состояние, сохраняя упругие свойства, а согласно крите­рию разрушения в материале не образуются трещины, приводящие к разрушению. В трехмерном пространстве главных напряжений 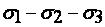условие (3.1) геометрически интерпретируется поверхно­стью, ограничивающей область безопасных напряженных состояний с точки зрения наступления текучести или реализации разрушения. Если выбрать систему координат, оси которой совпадают С направ­лением главных напряжений, то каждой точке ,

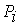пространства на­пряжении с координатами 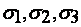соответствует определенное

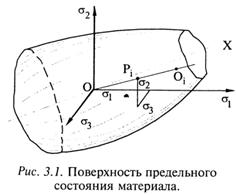
напряженное состояние (рис. 3.1). Процесс нагружения осуществляет­ся путем перехода от

состояния к состоянию .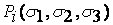

Путь нагружения может быть представлен отрезком 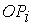. При неко­тором критическом значении главных напряжений наступает пре­дельное состояние материала. Это состояние отмечено точкой 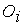. Совокупность точек 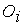образует поверхность, называемую предель­ной, так как она ограничивает область безопасных напряжений (внутри поверхности). В зависимости от механического состояния материала, стадии деформирования, нагружения и других факторов предельная поверхность может интерпретироваться поверхностью текучести или поверхностью разрушения.

В рамках классического подхода к проблеме разрушения сущест­венная роль напряженного состояния определяется тем, что его пара­метры и и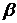спользуются для формулировки эквивалентных (предель­ных) напряженных состояний с различной степенью объем­ности на основе соответст­вующих гипотез прочности и результатов испытаний при простых (одноосных) видах нагружения.

В зависимости от того, какую физическую интерпретацию имеет критерии прочности 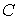, существующие теории прочности можно разделить на силовые, если критерий прочности выражается через нормальные или касательные напряжения, энергетические, если величина 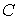имеет связь с удельной энергией деформации, и деформационные, если критерий связан с линейными удлинениями или деформациями.

Силовые теории прочности (теории наибольших нормальных напряжении, наибольших касательных напряжений, теория Мора) позволяют отразить различное сопротивление материалов растяжению и сжатию, и кроме того, теория наибольших касательных напряжений широко используется к качестве условия текучести:

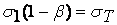(3.3)

Обобщение теории Мора на основе гипотезы Л. Надаи |33| о существовании функциональной связи между октаэдрическими касательными и нормальными напряжениями

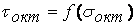(3.4)

позволило [34] путем введения обобщенных инвариантов тензора напряжении доказать, что каждый вид напряженного состояния определяется своим предельным семейством главных кругов и соответствующей им предельной кривой.

Более полно вид напряженного состояния описывают энергетические теории прочности, согласно которым предельное состояние в условиях текучести или разрушения наступает в результате достижения обшей энергией деформации или ее составляющей (энергией формоизменения) некоторого предельного значения. В основе этих теории лежит зависимость (3.4), а основное их различие состоит в разных путях учета влияния шаровою тензора напряжении на прочность материалов. Наибольшее распространение получила теория Губера — Мизеса — Генки, использующая в качестве условия текучести пластичных материалов соотношение

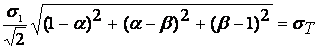(3.5)

Отражая с различной степенью точности предельное напряженное состояние, силовые и энергетические теории прочности не дают ответа на вопрос о характере разрушения, влиянии температуры и скорости нагружения, не учитывают степени пластической деформации. Влияние этих факторов в предположении о двух видах разрушения — хрупкого (отрывом) и вязкого (срезом) — анализируется на основе схем механического состояния [35,40].

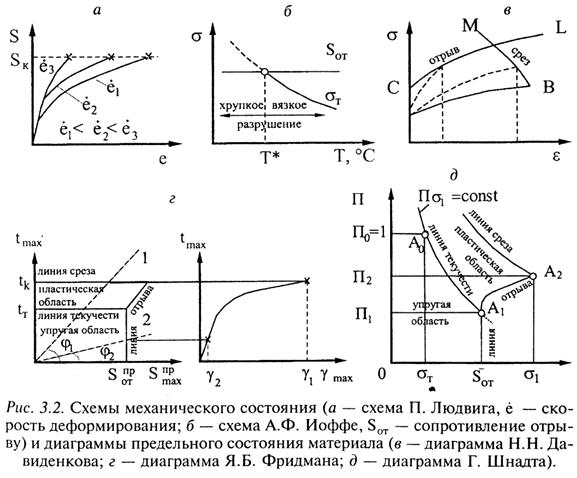
Переход от вязких разрушений к хрупким наблюдается в результате увеличения скорости деформирования (схема П. Людвига, рис. 3.2. а) или снижения температуры (схема Л.Ф. Иоффе, рис. 3.2, 6) и связан с повышением сопротивления пластическому деформированию, обусловливающего уменьшение предельной пластической деформации. Схема Н.Н. Давиденкова (рис. 3.2, в) определяет не только два характера разрушения, но и два вида сопротивления разрушению — сопротивление срезу (кривая МВ) при вязком разрушении и сопротивление отрыву (кривая CL) при хрупком разрушении. Обобщение этой схемы на случай сложного напряженного состояния дано Я.Б. Фридманом [40| при построении диаграммы механического состояния (рис. 3.2,г) в координатах 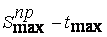( - максимальные истинные напряжения растяжения по 2-й гипотезе прочности; 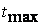— наибольшие касательные напряжения по 3-й гипотезе прочности) для данного напряженного состояния. В виде прямых линий наносятся предел текучести 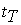, сопротивление сдвигу 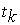, и сопротивление отрыву 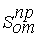. Вид напряженного состояния характеризуется функцией

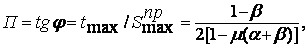(3.6)

где 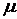— коэффициент Пуассона.

Если луч, соответствующий определенному значению 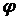, вначале пересекает линию 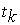, то разрушение происходит путем среза, если линию - то путем отрыва.

Диаграмма предельного состояния (рис. 3.2, д.). предложенная Г. Шнадтом [35], также определяет два вида разрушения — отрыв и срез, однако в качестве функции 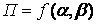принимается величина

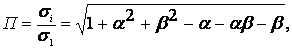
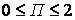(3.7)

По оси абсцисс откладывается наибольшее главное напряжение , являющееся мерой уровня напряженного состояния, а по оси ординат — интенсивность напряжений 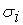, как мера влияния напряженного состояния на сопротивление материала пластическим деформациям. Линия текучести является уравнением параболы и характеризует изменение предела текучести при переходе от линейною напряженного состояния (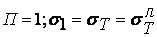) к объемному 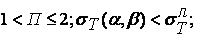(при при 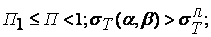), и согласно (3.5) и (3.7) получаем

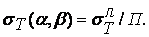(3.8)

С другой стороны, при использовании относительных напряжений 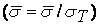и деформаций 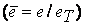условия возникновения пластических деформаций и случае линейного и объемного номинальных напряженных состояний в соответствии с (3.5) запишутся в виде

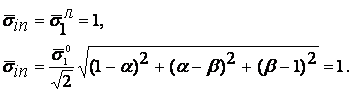(3.9)

Тогда коэффициент повышения первого главного напряжения при переходе от линейного номинального напряженного состояния к объемному номинальному будет равен

(3.10)

Из (3.7) и (3.10) следует, что , и подставляя это выражение в условие текучести (3.8), получим

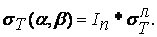(3.11)

Если в качестве условия текучести использовать (3.3), то величина определяется соотношением

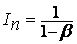(3.12)

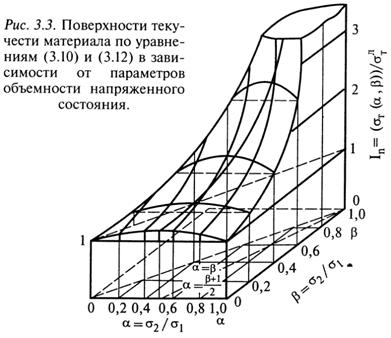
Изменение относительного предела текучести по уравнению (3.11) для трехосных однородных напряженных состояний, характеризуемых коэффициентами объемности на основе (3.10) и (3.12), Представляет собой поверхности текучести (рис. 3.3). С возрастанием 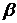при 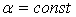поверхности поднимаются и с приближением к 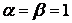(гидростатическое давление) устремляются к бесконечности. По критерию (3.3) коэффициент не зависит от , и поэтому линии поверхности текучести при 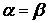параллельны оси (штриховые линии). Поверхность текучести на основе (3.5), (3.10), (3.11) совпадает с поверхностью по (3.3), (3.11), (3.12) только по крайним линиям при 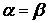, 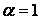и имеет выпуклость по средней линии 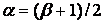на коэффициент 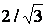. Изменение поверхности текучести при = 3 не имеет особого практического значения, так как однородные напряженные состояния такой степени объемности редко реализуются в действительности.

Деформационные теории прочности имеют ряд преимуществ по сравнению с силовыми и энергетическими теориями, так как критерии по напряжениям не позволяют учесть особенности, связанные с неоднородностью процессов деформирования и эффектами деформационной анизотропии.

Критерием разрушения в условиях развитых пластических деформаций может служить некоторое критическое значение деформации, характерное для данного материала и условий деформирования. При одноосном растяжении разрушающая деформация (предельная пластичность) равна

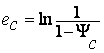(3.13)

где 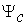— относительное сужение при разрушении.

Как показывают экспериментальные исследования, предельная пластичность возрастает в условиях гидростатического давления |41, 42| и уменьшается с увеличением параметров и 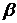, т.е. при переходе от одноосного напряженного состояния к плоскому и объемному [33, 36, 41, 43-45]. Количественное определение влияния объемности напряженного состоянии на сопротивление пластическим деформациям и на предельные нагрузки [44-46], а также анализ предельных разрушающих деформаций в связи с неодноосностью напряженного состояния [37, 47, 48] показали, что предельные пластические деформации при разрушении в условиях неодноосного напряженного состояния определяются отношением гидростатического давления 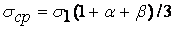к интенсивности напряжений 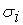.Согласно результатам исследований, выполненных в |49], коэффициент снижения предельных пластических деформаций 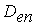, равный отношению интенсивности деформации при разрушении для объемного 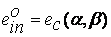и линейного напряженных состояний, с учетом (3.10) записывается в виде

(3.14)

где 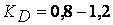— характеристика материала.

Тогда предельная пластическая деформация при неодноосных напряженных состояниях определяется выражением

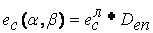. (3.15)

Таким образом, условие наступления пластических деформаций, характеризуемое пределом текучести 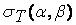, и разрушающая пластическая деформация при неодноосных номинальных напряженных состояниях определяются через предел текучести 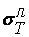и разрушающую деформацию при одноосном (линейном) напряженном состоянии и параметры жесткости напряженного состояния. Отсюда следует, что величины 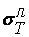и являются основополагающими характеристиками предельных состояний материалов дли различных видов напряженно-деформированных состояний. Их значения определяются экспериментально по результатам испытаний гладких образцов на осевое растяжение в соответствии с ГОСТ 1497-84 [50]