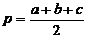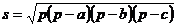Составить алгоритм вычисления функции

ЛЕКЦИЯ № 6.

6. ЭТАПЫРЕШЕНИЯ ЗАДАЧ НА ЭВМ.

Подготовка задачи к решению на ЭВМ является достаточно сложной процедурой, включающей следующие этапы:

1. Содержательная постановка задачи - определение цели и условий решения задачи (выполняется специалистом той области, к которой относится данная задача).

2. Математическая формулировка задачи - построение математической модели (описание связей между объектами задачи математическими соотношениями).

3. Выбор существующего или разработка нового метода решения задачи.

4. Разработка алгоритма решения задачи - отображение математических операций в определенную последовательность действий ЭВМ.

5. Программирование - запись алгоритма изобразительными средствами конкретного языка программирования.

6. Подготовка информации - перенесение текста программы и исходных данных на носитель информации с помощью специальных устройств подготовки информации.

7. Отладка программы, включая визуальный и синтаксический контроль, решение контрольного примера.

8. Решение задачи на ЭВМ и получение результата.

Эффективное использование ЭВМ требует от пользователя умения программировать на каком-либо алгоритмическом языке. Наиболее распространенными в настоящее время являются следующие языки программирования: Бейсик, Фортран, Паскаль.

Необходимо отметить, что разработка программы - многоступенчатый процесс, и начинается он вовсе не с сидения перед машиной. Более того, половина всей работы вообще выполняется за столом и не требует общения с ЭВМ. Исключительно важна общая четкая организация работы, логичность действий на всех этапах, тщательность их исполнения, готовность к неоднократной переделке ошибочных или сомнительных мест в программе. Но все окупается, когда программа, наконец, заработает.

Не следует считать, что компьютеру может быть понятно что-либо «само собой». Приступая к решению задачи, необходимо выяснить имеющиеся в распоряжении пользователя возможности - это равносильно сведениям о том, что и на каком языке компьютер «понимает».

В зависимости от решаемой задачи следует выбирать определенную компьютерную систему. Эти системы, как правило, ориентированы на класс решаемых задач, например: системы обработки данных, системы обработки текстов, графический редактор и т.д.

Умение решать практические задачи с помощью компьютера означает:

n вовремя находить и вычленять практические проблемные ситуации;

n правильно ставить задачу, выбирая соответствующее знаковое оформление;

n строить формализованное описание задачи или предметной области так, как это необходимо для используемой системы, т.е. с учетом ее сервисных и рабочих средств; соотносить модель задачи, отражающую ее понимание пользователем, со средствами решения, которые представляет компьютер - языком программирования, сервисными возможностями системы, объемом памяти, структурой данных и т.д.;

n планировать и намечать стратегию решения, уметь адекватно использовать имеющиеся средства программного обеспечения и из них конструировать алгоритм решения;

n учитывать соотношение цены реального времени в зависимости от важности задачи.

В качестве помощника компьютер тем эффективнее, чем лучше и глубже пользователь осознает решаемую задачу. Постановка и анализ задач выполняется человеком. Это способствует творческому подходу к делу, творческому мышлению, совершенствованию профессиональной деятельности.

6.1. ПОНЯТИЕ АЛГОРИТМА.

В течение жизни каждый человек постоянно пользуется набором всевозможных алгоритмов - правил, которые заложены в него природой, даны воспитанием, обучением, тренировкой, выработаны на основе собственного опыта. Инструкции пользования лифтом, телефоном, различными автоматами и бытовыми приборами, правила перехода улицы, оказание первой медицинской помощи, распорядок дня, кулинарные рецепты, порядок проведения физических и химических опытов, правила вычислений, методы решения алгебраических и геометрических задач - все это можно считать алгоритмами.

Алгоритм – одно из основных математических понятий. Происхождение термина «алгоритм» связывают с именем великого узбекского математика и астронома аль-Хорезми, жившего в IX веке и разработавшего правила выполнения четырех арифметических действий над числами в десятичной системе счисления. Множества этих правил назвали алгоритмом (algorithmi - от латинского написания имени аль-Хорезми), а затем словом «алгоритм» стали обозначать совокупность правил определенного вида, а не только правил выполнения арифметических действий.

Долгое время понятие алгоритма использовалось исключительно математиками, обозначая правила решения различных задач. Развитие математической науки привело к необходимости уточнения алгоритма - одного из основных, базовых математических понятий, к разработке новой математической дисциплины «теории алгоритмов». Теория алгоритмов как предмет изучения дает возможность алгоритмы разрабатывать, анализировать и преобразовывать на научной, математической основе.

Большое значение понятия алгоритма стало особенно очевидным в связи с развитием электронно-вычислительной техники и программирования. Оказалось, что составление алгоритма является необходимым этапом решения задач при помощи ЭВМ.

Теперь слово «алгоритм» вышло далеко за пределы математики, можно без преувеличения сказать, что мы живем в мире алгоритмов. Ныне алгоритмом называют любую точно определенную последовательность действий (не обязательно математических!), необходимых для выполнения некоторой работы или для решения данной задачи.

Для эффективного пользования алгоритмами важно представлять себе все задание в целом и уметь разбивать на частные задачи, на отдельные этапы, на стандартные операции, правильная последовательность выполнения которых приведет (или должна привести) к желаемому результату.

Среди математиков популярна следующая притча-задача, ярко иллюстрирующая алгоритмический способ мышления.

Вопрос:

Имеется газовая плита, спички, водопровод, чайник. Как вскипятить чай?

Ответ:

С помощью водопровода наполнить чайник, с помощью спичек зажечь газовую горелку, поставить чайник на газ. Через несколько минут он закипит.

Вопрос:

Допустим, что чайник уже наполнен, газ уже горит. Как выполнить задание теперь?

Ответ:

Выключить газ, вылить из чайника воду - и мы сведем задачу к предыдущей, решение которой уже известно.

При всей своей кажущейся нелепости эта притча имеет глубокий смысл. Если предлагаемая задача (не только математическая) может быть сведена к другой, решение которой известно, то и предлагаемую задачу можно решить тем же способом. Возможно, что этот способ окажется не самым простым, не самым коротким, но решить задачу с его помощью можно!

Для решения задачи на ЭВМ необходимо выбранный метод ее решения выразить в виде определенной последовательности операций, выполняемых вычислительной машиной. При этом следует детально описать решение задачи, предусмотрев все возможные случаи, переходы и проверки. Этот этап можно определить как разработку решения задачи.

Алгоритм представляет собой описание вычислительного процесса, ведущего от варьируемых начальных данных к искомому результату.

Правильно разработанный алгоритм должен обладать следующими свойствами:

n определенностью или детерминированностью - применение алгоритма к одним и тем же исходным данным должно приводить к одному и тому же результату. Это свойство связано с необходимостью его однозначного понимания, отсутствия какой бы то ни было неопределенности в трактовке алгоритма;

n массовостью – каждый алгоритм решает не одну отдельную задачу, а определенный класс задач. Конкретные задачи этого класса отличаются одна от другой системой своих начальных величин;

n дискретностью - возможность расчленить его на конечное количество отдельных «элементарных» шагов;

n результативностью - возможность достижения результата за конечное число достаточно простых шагов, перерабатывая начальные данные в решении задачи, или доказать, что алгоритм неприменим к данному множеству исходных данных. Наибольшее множество начальных данных, на котором данный алгоритм есть результативным, называют областью применения алгоритма.

Применение алгоритма к конкретным исходным данным из области применения алгоритма называется алгоритмическим процессом. Этот процесс основывается в переработке входной информации (начальных данных) в решение задачи по правилам (командам), которые определяются данным алгоритмом.

Пример.

Отгадать задуманное число. Предложить задумать какое-нибудь натуральное число х и выполнить следующие операции:

а) умножить число х на 10;

б) к результату прибавить число 5;

в) полученную сумму удвоить;

г) сообщить полученное число.

Зная полученное число m можно отгадать задуманное число х, используя следующий алгоритм:

1) разделить число m на 10, перейти к пункту 2;

2) от результата отнять единицу, перейти к пункту 3;

3) полученный результат разделить на 2.

Это и будет задуманное число х.

Алгоритмом наз. некоторая конечная последовательность предписаний (правил), однозначно определяющих процесс преобразования исходных и промежуточных данных в результат решения задачи.

Корректность алгоритма состоит в получении правильного решения для всех допустимых исходных данных.

Формальность – очень важная черта каждого алгоритма. Именно благодаря этому исполнение алгоритма можно поручить любому автомату, который «умеет» точно выполнять команды алгоритма.

Задача построения и применения алгоритма связана с использованием двух языков: одним описывается алгоритм, другим – информацию, которая подлежит переработке согласно данному алгоритму. Объекты, над которыми производят указанные в алгоритме операции, называются операндами.

Разработка алгоритма решения задачи является очень ответственным этапом при подготовке задачи к решению на ЭВМ. Ошибки, допущенные на этапе разработки алгоритма, приведут к тому, что написанная по этому алгоритму программа будет неработоспособной, т.е. не позволит получить правильный результат.

В частности, для удовлетворения свойств массовости и результативности алгоритма необходимо, чтобы результат мог быть получен для любого множества исходных данных, если на них не накладываются ограничения условиями задачи. Это означает, что при построении алгоритма необходимо предусмотреть те варианты исходных данных, при которых возникают «невычислительные» ситуации - деление на ноль, вычисление корня четной степени из отрицательного числа, вычисление логарифма отрицательного или равного нулю аргумента и т.д. - и выдавать информацию о возникновении такой ситуации в качестве результата.

Алгоритм решения задачи можно описать различными способами: с помощью словесной записи, в виде блок-схемы или в операторной форме.

Словесная запись алгоритма представляет собой перечисление простейших действий (арифметических, логических и других), которые нужно выполнить для получения результата, в той последовательности, в какой они должны выполняться.

Операторная запись алгоритма представляет собой изображение алгоритма в виде последовательности операторов какого-либо алгоритмического языка.

Описание алгоритма в виде блок-схем является наиболее наглядным способом представления алгоритмов. Алгоритм при этом изображается в виде последовательности блоков, предписывающих выполнение отдельных функций, и связей между ними. Внутри блоков помещается информация, поясняющая выполняемые ими действия. Каждый блок снабжен номером, который размещается в разрыве контура в левой верхней его части. В таблице приведены некоторые наиболее часто используемые блоки и пояснения выполняемых ими функций.

Схемою алгоритма называют графическое задание алгоритма в виде совокупности условных графических обозначений – символов, соединенных между собой стрелками (горизонтальными и вертикальными линиями потока), которые однозначно устанавливают последовательность выполнения операций, записанных в этих символах. Каждый символ (блок) выполняет определенную операцию и обеспечивает определенный этап переработки информации. Среди этих блоков есть первый, с которого начинает работать алгоритм, и есть последний, после выполнения которого действия алгоритма прекращаются. Направление линий потока сверху вниз и слева направо берут за основное и стрелками может не обозначаться. Направление линий потока справа налево и снизу вверх указывают стрелками. Место соединения линий потока обозначают точкой.

В середине символа «Процесс» (арифметический блок) можно записать правило (команду) алгоритма математической формулой. В середине символа «Решение» (логический блок) записывается логическое условие (отношение). Если это условие истинно, то выполняется та операция алгоритма, к символу которого ведет стрелка с обозначением «да», в противном случае, выполняется операция алгоритма, к которой проведена стрелка с обозначением «нет». В блоке ввода информации после символа «Ввод» перечисляются через запятую те переменные, которые должны иметь конкретные числовые значения до начала выполнения алгоритма. В блоке вывода информации после символа «Вывод» перечисляются через запятую те переменные, которые получают числовые значения в результате решения задачи по данному алгоритму.

УСЛОВНЫЕ ГРАФИЧЕСКИЕ ОБОЗНАЧЕНИЯ, ПРИМЕНЯЕМЫЕ ПРИ СОСТАВЛЕНИИ СХЕМ АЛГОРИТМОВ.

№ п/п	Название символа	Символ	Отображаемая функция
1	Блок вычислений (процесс)		Вычислительное действие или последователь-ность вычисли-тельных действий
2	Логический блок (решение)		Выбор направления выполнения алгоритма в зависимости от некоторых условий (условия)
3	Блоки ввода-вывода		Общее обозначение ввода или вывода данных (в незави-симости от физи-ческого носителя)
	Вывод данных, носителем кото-рых служит доку-мент (печатающее устройство)
	Начало-конец (вход – выход)		Начало или конец программы, оста-нов, вход или выход в подпрог-раммах
5	Предопределён­ный процесс (подпрограмма)		Вычисления по стандартной под-программе или подпрограмме пользователя
6	Блок модификации (заголовок цикла)		Выполнение действий, изменяющих пункты алгоритма
7	Соединитель		Указание связи между прерванными линиями потока информации в пределах одной страницы
8	Межстранич-ный соединитель		Указание связи между частями схемы, расположенными на разных листах

Никаких строгих правил разбиения алгоритма на отдельные блоки при построении схем не существует. В блоки можно выделять отдельные арифметические действия, вычисления по формулам и даже отдельные алгоритмы, которые решают более узкие классы задач. Основным преимуществом представления алгоритмов в виде блок-схем является то, что не требуется дополнительных пояснений, имеется возможность наглядно представить последовательность действий, необходимых для решения задачи. В связи с этим изображение алгоритмов в виде блок-схем используется в настоящее время наиболее широко.

6.2. ОСНОВНЫЕ ТИПЫАЛГОРИТМОВ

По характеру связей между выполняемыми в алгоритме операциями различают линейные, разветвляющиеся и циклические алгоритмы.

6.2.1. ЛИНЕЙНЫЕ АЛГОРИТМЫ

Наиболее простыми по своей структуре являются алгоритмы, в которых все операции выполняются последовательно в порядке их расположения в алгоритме. Такой порядок следования называется естественным. Алгоритм с естественным порядком выполнения операций называется линейным.

Задача 1.

Дан треугольник со сторонами a, b, c. Найти площадь треугольника по формуле Герона 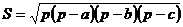, где p – полупериметр треугольника. Составить блок-схему.

Решение:

Нача

 

 

 

 

 

 

 

 

 

 

 

 

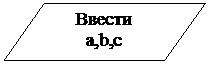6.2.2. АЛГОРИТМЫРАЗВЕТВЛЯЮЩЕЙСЯ СТРУКТУРЫ

Решение ряда практических задач не ограничивается линейным алгоритмом, а предусматривает различные пути вычисления решения. Причем выбор того или иного пути определяется либо условиями задачи, либо результатами, полученными в процессе решения. Каждое из возможных направлений вычисления называется ветвью, в зависимости от выполнения некоторого условия вычислительный процесс может идти по одной или другой ветви. Алгоритм такого вычислительного процесса называется разветвляющимся алгоритмом. Количество ветвей в общем случае может быть больше двух.

Задача 2.

Составить алгоритм вычисления функции

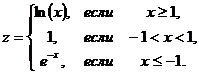
Решение: Вычислительный процесс в данном случае имеет три ветви. Выполнение условия 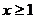определяет вид выражения для вычисления функции z, т.е. позволяет реализовать первую ветвь. Чтобы установить, по какой из двух оставшихся ветвей должен идти вычислительный процесс в случае невыполнения первого условия, необходимо сделать еще одну проверку.

 

 

 

 

Y=ln(x)

да

 

нет

Y=

да

 

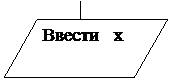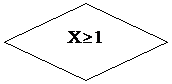
нет

 

 

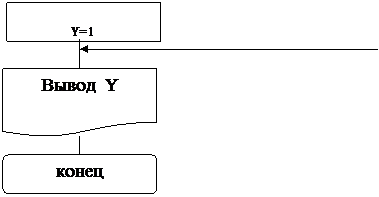6.2.3. АЛГОРИТМЫЦИКЛИЧЕСКОЙ СТРУКТУРЫ

Циклическим алгоритмом называется алгоритм, который дает возможность получить результат многоразовым повторением определенной последовательности действий, которая называется циклом. Если число повторений цикла задано, то такие циклы называются арифметическими. Если количество повторений цикла заранее неизвестно, а определяется только в процессе выполнения алгоритма, то такие циклы называются итерационными.

АРИФМЕТИЧЕСКИЕ ЦИКЛЫ

Типичным примером такого алгоритма является алгоритм решения задачи табулирования функции одной переменной, которая формулируется следующим образом.

Задача 3.

Вычислить значение функции 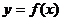некоторой переменной 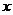, изменяющейся от начального значения 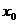до конечного 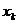с постоянным шагом .

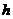Решение: Эта задача реализуется с помощью цикла с заданным количеством повторений, которое определяется как 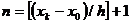. Здесь величина в квадратных скобках означает целую часть от частного. Процедура вычислений сводится к следующему: вычисляется значение 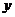для начального значения 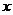, равного 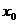. Затем 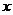увеличивается на значение шага 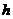, и для него вычисляется значение 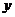. Последний этап повторяется до тех пор, пока 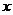не превысит конечного значения .

 

 

 

x=

y=f(x)

 

 

 

 

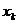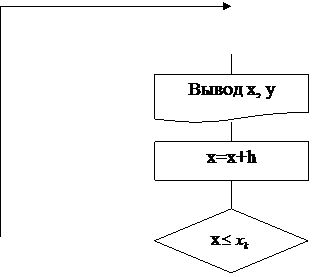
да

нет

 

ИТЕРАЦИОННЫЕ ЦИКЛЫ

Такие алгоритмы характеризуются последовательным приближением вычисляемых величин к искомому значению. Окончание цикла в этом случае обычно осуществляется при достижении заданной точности вычисления результата. К итерационным циклам приводят задачи вычисления сумм бесконечных рядов, реализации численных методов решения уравнений, систем уравнений, задачи оптимизации.

Рассмотрим правила составления итерационных циклических алгоритмов на примере вычисления суммы бесконечного ряда. Задача при этом сводится к нахождению с погрешностью, не превышающей 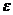, суммы

,

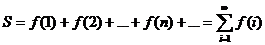каждое слагаемое которой является функцией номера 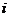, а также может являться функцией одного или нескольких дополнительных параметров.

Задача нахождения такой суммы является типичным примером итерационного процесса, так как заранее не известно, при каком номере слагаемого будет достигнута требуемая точность.

Вычисление суммы членов бесконечного ряда возможно лишь в том случае, если получаемая в результате циклического процесса последовательность s(1), s(2), …, s(i), … сходится к своему предельному значению S, т.е. существует предел 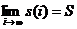. Здесь s(i) – сумма i членов бесконечного ряда.

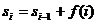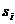Процесс вычисления суммы членов равномерно сходящегося ряда организуется в виде циклического алгоритма, когда при каждом прохождении цикла номер слагаемого i увеличивается на единицу, а сумма изменяется на величину i-го слагаемого, т.е. , где и 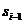- суммы i и i-1 слагаемых. Приведенное выше соотношение в алгоритме вычисления записывается следующим образом: S=S+f(i), что означает добавление слагаемого с номером i к значению суммы, вычисленному на предыдущем шаге алгоритма, и присвоение вычисленного значения S+f(i) той же переменной S. Начальное значение S должно быть равно нулю, в этом случае после первого выполнения цикла значение S будет равно значению первого слагаемого. Суммирование считается законченным при выполнении условия 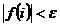, т.е. если значение очередного вычисленного члена ряда меньше величины погрешности.

Задача 4.