Приближённые методы вычисления

Контрольная работа

По дисциплине «ЭВМ-эксперимент и машинная обработка информации»

Тема: Численное интегрирование

Аннотация

В данной работе будут рассмотрены три метода приближённого интегрирования определённого интеграла: метод прямоугольников, метод трапеций и метод Симпсона. Все эти методы будут подробно выведены с оценкой погрешности каждого из них. В работу включено наглядное применение нахождения определенного интеграла методом прямоугольников и трапеций. В материале имеются иллюстрации, с помощью которых, можно более глубоко вникнуть в суть рассматриваемой темы.

Введение

Основная цель этой работы заключается в ознакомлении с численным интегрированием. Суть численного интегрирования заключается в том, что подынтегральную функцию заменяют другой приближенной функцией, так, чтобы, во-первых, она была близка к первоначальной функции и, во вторых, интеграл от нее легко вычислялся. Методы численного интегрирования, основаны на замене подынтегральной функции интерполяционным многочленом. Это позволяет приближенно заменить определенный интеграл интерполяционной суммой. В зависимости от способа ее вычисления получаются разные методы численного интегрирования, такие как:

метод прямоугольников;

метод трапеций;

метод Симпсона.

В частности при выполнении данной работы использовался метод трапеций.

Математическая модель

Определение интеграла и его геометрический смысл

В начале узнаем, что такое определённый интеграл. Возможны два различных подхода к определению определённого интеграла. Приращение любой из преобразованных функций при изменении аргумента от до 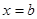называют определённым интегралом от a до b функции f и обозначается 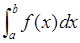. Причём функция является первообразной для функции f на некотором промежутке D, а числа а и b принадлежат этому промежутку. Это можно записать следующим образом:

(1)

это формула Ньютона-Лейбница.

Рис. 1

Если при любой последовательности разбиений отрезка [a;b] таких, что (n→∞) и при любом выборе точек 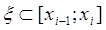интегральная сумма 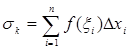стремится к одному и тому же конечному пределу А, то это число А и есть определённый интеграл, т.е.

(2)

Где 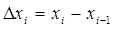- начало разбиения произвольная точка из отрезка сумма всех произведений . Простыми словами, определенный интеграл есть предел интегральной суммы, число членов которой неограниченно возрастает, а каждое слагаемое стремится к нулю.

Геометрический смысл

Рис. 2

Всякая непрерывная на отрезке [a,b] функция f интегрируема на отрезке [a,b], функция f неотрицательна, но определённый интеграл численно равен S криволинейной трапеции, ограниченной графиком функции f, осью абсцисс и прямыми

и , .

Приближённые методы вычисления

Как мы уже отметили, если функция f непрерывна на промежутке, то на этом промежутке существует функция такая, что , то есть существует первообразная для функции , но не всякая элементарная функция имеет элементарную первообразную . Объясним понятие элементарной функции.

Функции: степенная, показательная, тригонометрическая, логарифмическая, обратные тригонометрическим называются основными элементарными функциями. Элементарной функцией называется функция, которая может быть задана с помощью формулы, содержащей лишь конечное число арифметических операций и суперпозиций основных элементарных.

Бывает, что на практике сталкиваются с вычислением интегралов от функций, которые заданы табличными и графическими способами, или интегралы от функций, первообразные которых выражаются через элементарные функции очень сложно, что неудобно, долго и не рационально. В этих случаях вычисление определённого интеграла по формуле Ньютона-Лейбница (1) сводит вычисление определённого интеграла от какой-либо функции к нахождению её первообразной. Значит, если первообразная не элементарна, надо вычислить определённый интеграл как-то по другому, поэтому прибегают к различным методам приближённого интегрирования.

В основе приближённых методов интегрирования лежит геометрический смысл определённого интеграла, который рассмотрен выше.

Формул приближённого интегрирования существует много. В данной курсовой работе будет рассмотрено три метода приближённого интегрирования: метод трапеций, метод прямоугольников и метод Симпсона.

Формула прямоугольников

Теперь рассмотрим первый вид приближённого вычисления:
требуется вычислить определённый интеграл: .

Пусть на отрезке [a,b] задана непрерывная функция . Разделим отрезок [a,b], аналогично как в формуле трапеций: точками на n равных частей длины , где .

Рис. 3

Обозначим через y0,y1,y2,…,yn-1,yn значение функции 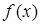в точках то есть, если записать в наглядной формуле:

В данном способе подынтегральную функцию заменяем функцией, которая имеет ступенчатый вид (на рис. выделена).

Составим суммы:

; .

Каждое слагаемое этих сумм выражает площадь, полученных прямоугольников с основанием .

Каждая из этих сумм является интегральной суммой для на отрезке [a,b], и равна площади ступенчатых фигур, а значит приближённо выражает интеграл. Вынесем из каждой суммы, получим:

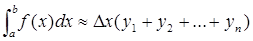
Выразив x, получим окончательно:

(3)

(3*)

Это и есть формулы прямоугольников. Их две, так как можно использовать два способа замены подынтегральной функции. Если - положительная и возрастающая функция, то формула (3) выражает S фигуры, расположенной под графиком, составленной из входящих прямоугольников, а формула (3*) - площадь ступенчатой фигуры, расположенной под графиком функции составленной из выходящих треугольников.

Ошибка, совершаемая при вычислении интегралов по формуле прямоугольников, будет тем меньше, чем больше число n (то есть чем меньше шаг деления)

Для вычисления погрешности этого метода используется формула:

, где

Результат полученный по формуле (3) заведомо даёт большую площадь прямоугольника, так же по формуле (3*) даёт заведомо меньшую площадь, для получения среднего результата используется формула средних прямоугольников:

(3**)

Формула трапеций.

Рис. 4

Возьмём определённый интеграл

где - непрерывная подынтегральная функция, которую мы для наглядности будем предполагать положительной. При вычислении интеграла с помощью формулы трапеций подынтегральная функция заменяется функцией, график которой представляет собой ломанную линию (на рис. 1 красным цветом), звенья которой соединяют концы ординат и Тогда площадь криволинейной трапеции, ограниченной линиями x=a, , , , а значит (следуя из геометрического смысла), и значение нужного нам интеграла, приблизительно равна сумме площадей обычных трапеций с основаниями и , и высотой , так как (если более привычно выражать для нас) это ,a 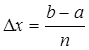при делении отрезка на n равных отрезков при помощи точек . Прямые разбивают криволинейную трапецию на n полосок. Принимая каждую из этих полосок за обыкновенную трапецию, получаем, что площадь криволинейной трапеции приблизительно равна сумме обыкновенных трапеций.

Рис. 5

Площадь крайней полоски слева, как помниться из школьного курса геометрии, равна произведению полусуммы основания на высоту.

Итак, запишем сказанное выше в математическом виде:

(4)

Формула (4) и есть формула трапеций

Для определения погрешности интеграла вычисленного с помощью формулы трапеций используется формула:

, где

Формула Симпсона (формула парабол).

Существует два подхода к формуле Симпсона. В одном используется парабола в другом нет.

А) с использованием параболы.

Разделим отрезок [a;b] на чётное число равных частей . Площадь криволинейной трапеции, соответствующей первым двум отрезкам [x0,x1], [x1,x2] и ограниченной заданной кривой , заменим площадью криволинейной трапеции, которая ограничена параболой второй степени, проходящей через три точки M0[x0,y0], M1[x1,y1], M2[x2,y2] и имеющей ось, параллельную оси Oy. Такую криволинейную трапецию называют параболической трапецией.

Уравнение параболы с осью, параллельной оси Oy, имеет вид:

Рис. 6

Коэффициенты A, B и C однозначно определяются из условия, что парабола проходит через три заданные точки. Аналогичные параболы строятся и для других пар отрезков. Сумма параболических трапеций и даст приближённое значение интеграла. Сначала вычислим площадь одной параболической трапеции. Для этого докажем лемму.

Лемма: если криволинейная трапеция ограничена параболой , осью Ox и двумя ординатами, расстояние между которыми равно 2h, то её площадь равна:

(5)

где и 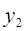- крайние ординаты, а - ордината кривой в середине отрезка.

Рис. 7

Доказательство:

Расположим вспомогательную систему координат так, как показано на рис. Коэффициент в уравнение параболы определяются из следующих уравнений:

Если 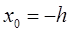, то

Если , то (6)

Если , то

Считая коэффициенты A, B, C известными определим площадь параболической трапеции с помощью определённого интеграла:

из равенства (6) следует, что

следовательно:

ч.т.д. пользуясь формулой (5), можно написать приближённые равенства, учитывая, что

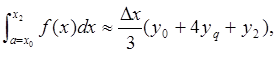
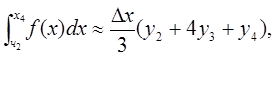
складывая левые и правые части, получим слева искомый интеграл, справа его приближённое значение:

или

(7)

Это и есть формула Симпсона. Здесь число точек деления произвольно, но чем это число больше, тем точнее сумма в правой части равенства (6) даёт значение интеграла. Формула Симпсона даёт самое точное значение интеграла (из классических формул приближённого интегрирования), погрешность для этого метода находится по формуле:

где

Б) Без использования парабол

Рис. 8

В тех случаях, когда линия между и мало изогнута, интеграл приближенно выражается достаточно простой формулой. Будем считать положительной и искать площадь криволинейной трапеции aABb. Для этого разделим отрезок [a;b] точкой

пополам и в точке проведём касательную к линии . После этого разделим [a,b] точками p и g на 3 равные части и проведём через них прямые и . P и Q - точки пересечения прямых с касательной. Соединив AP и BQ, получим 3 прямолинейные трапеции aAPp, pPQq, qQBb. Сумма площадей этих трапеций равна будет примерно равна площади криволинейной трапеции aABb:

Обозначим: Aa, Pp, qQ, bB - основания трапеций;

- высота трапеций, в данном случае число n строго задано n=3

Получаем:

(8)

Обозначим, что: , . Отрезки pP и qQ не являются ординатами точек линии , так как P и Q лежат на касательной. Но нам нужна сумма этих отрезков, которая выражается через среднюю линию трапеции и равна полусумме её оснований, откуда

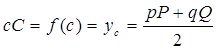Значит . Формула (8) принимает вид:

(9)

Эта формула называется малой формулой Симпсона.

Рис. 9

Малая формула Симпсона пригодна, когда график подынтегральной функции мало изогнут, например, для случая, изображённого на рисунке, применять малую формулу уже нельзя, так как она даёт значение 0 на [a,b]. Но если отрезок [a,b] разбить на части [a,c] и [c,b] и к каждому из них применить формулу (9), то получится приемлемый результат.

Эта идея лежит в основе вывода «большой» формулы Симпсона.

Для вычисления интеграла выберем какое-либо чётное число и разложим [a,b] на n равных частей точками

Интеграл представим в виде суммы

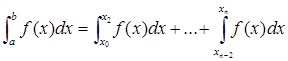
К каждому слагаемому справа применим малую формулу Симпсона. Учитывая, что в каждом интеграле длина промежутка интегрирования , и положить , то получим:

Раскроем скобки:

Это и есть «большая формула Симпсона». Её точность, также как и у всех формул рассмотренных выше, тем выше, чем больше n. Эта формула совпадает с формулой (7), выведенной с помощью парабол. Для оценки погрешности формулы Симпсона используется формула:

метод парабола интеграл мatlab