Программа для вычисления значения интеграла методом трапеций в среде пакета Matlab:
function y=int_trapezoidal(n,a,b)(mod(n,2)~=1)=(b-a)/n;=a:h:b;=0;i=1:n/2=s+f(x(2*i-1))+2*f(x(2*i))+f(x(2*i+1));=s*h/2;=3.051757810013100e-005;
disp ('Количество элементарных отрезков: '), disp(n)('Результат: '), disp (y)('Погрешность: '), disp (erf)disp ('Введите четное число!')
endy=f(x)
y=4/(1+x^2);
Цикл if отвечает за то, что если пользователь введет число n элементарных отрезков не кратных двум, программа выведет на экран сообщение:
Введите четное число!

Рис. 10
Цикл for - это основная составляющая программы для данного метода. Здесь суммируется площади трапеций, на которые разбивается наша площадь под кривой.
Погрешность erf  3.0517e-005 была получена как разность результатов с n = 64 и n = 128 элементарными отрезками.
3.0517e-005 была получена как разность результатов с n = 64 и n = 128 элементарными отрезками.
Таблица полученных результатов
| n, коли-во эл. отрезков | Значение интеграла |
| 3.100000000000000 | |
| 3.131176470588235 | |
| 3.138988494491089 | |
| 3.140941612041389 | |
| 3.141429893174975 | |
| 3.141551963485653 | |
| 3.141582481063753 |
Даже при n = 128 ответ является точным лишь до пятого знака после запятой (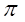 =3,141592653589793 - точное значение числа пи для 15 знаков после запятой).
=3,141592653589793 - точное значение числа пи для 15 знаков после запятой).
Только при n = 700000 значение числа 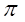 совпадает с точным значением до 13 знака после запятой.
совпадает с точным значением до 13 знака после запятой.
Определение значения интеграла с помощью метода прямоугольников. Сравнение результатов
Программа для вычисления значения интеграла методом прямоугольников в среде пакета Matlab:
function s = int_rectangle(n,a,b)= (b-a)/n;= 0;= a:h:b;i = 1:n= s+f(x(i))*h;y = f(x)
y = 4/(1+x^2);
Таблица полученных результатов
| n, коли-во эл. отрезков | Значение интеграла |
| 3.600000000000000 | |
| 3.381176470588235 | |
| 3.263988494491089 | |
| 3.203441612041389 | |
| 3.172679893174975 | |
| 3.157176963485654 | |
| 3.149394981063753 |
Очевидно, что метод прямоугольников значительно уступает точностью методу трапеций с одинаковым количеством элементарных отрезков n.
Погрешность данного метода составляет 7.781982421901e-003, что на два порядка больше, чем погрешность метода трапеций.
Использование для вычисления одновременно двух методов (трапеций и прямоугольников) позволило исследовать зависимость точности вычислений при применении обоих методов.
Следовательно, при понижении численного значения точности, вычислений результаты расчетов по обеим методам стремятся друг к другу и оба к точному результату.
Заключение
В завершении работы, хочется отметить ряд особенностей применения рассмотренных выше методов. Каждый способ приближённого решения определённого интеграла имеет свои преимущества и недостатки, в зависимости от поставленной задачи следует использовать конкретные методы. Если необходимо быстро получить решение, но нет необходимости в большой точности ответа, следует воспользоваться методом прямоугольников. Если же необходимо получить наиболее точный результат, идеально подходит метод Симпсона. Метод трапеций даёт ответ более точный, чем метод прямоугольников, но методу Симпсона он сильно уступает, этот метод можно назвать «золотой серединой» между двумя другими.
Список литературы
1. Каханер Д., Моулер К., Нэш С. Численные методы и программное обеспечение. - М.: Мир, 2011. - 575 с.
2. Форсайт Дж., Малькольм М., Моулер Машинные методы математических вычислений. - М.: Мир 2009. - 277 с.
. Зализняк В.Е. Основы научных вычислений. Введение в численные методы для физиков. - М.: Едиториал УРСС, 2012. - 296 с.