Многогранники
Многогранник – это такое тело, поверхность которого состоит из конечного числа плоских многоугольников.
Многогранник называется выпуклым, если он расположен по одну сторону плоскости каждого плоского многоугольника на его поверхности. Общая часть такой плоскости и поверхности выпуклого многогранника называется гранью. Грани выпуклого многогранника являются плоскими выпуклыми многоугольниками. Стороны граней называются ребрами многогранника, а вершины – вершинами многогранника.
Простейшие многогранники: куб, призма, пирамида.
Призма
Призмой называется многогранник, который состоит из двух плоских многоугольников, лежащих в разных плоскостях и совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих многоугольников. Многоугольники называютсяоснованиями призмы, а отрезки, соединяющие соответствующие вершины, - боковыми ребрами призмы.  Свойства призмы: 1. Основания призмы равны и лежат в параллельных плоскостях. 2. Боковые ребра параллельны и равны. Поверхность призмы состоит из оснований и боковой поверхности. Боковая поверхность состоит из параллелограммов. Высотой призмы называется расстояние между плоскостями. Отрезок, соединяющий две вершины призмы, не принадлежащие одной грани, называется диагональю призмы. Свойства призмы: 1. Основания призмы равны и лежат в параллельных плоскостях. 2. Боковые ребра параллельны и равны. Поверхность призмы состоит из оснований и боковой поверхности. Боковая поверхность состоит из параллелограммов. Высотой призмы называется расстояние между плоскостями. Отрезок, соединяющий две вершины призмы, не принадлежащие одной грани, называется диагональю призмы.
| |
Прямая призма

Призма называется прямой, если ее боковые ребра перпендикулярны основаниям.
Призма называется наклонной, если ее боковые ребра не перпендикулярны основаниям.
У прямой призмы грани – прямоугольники.

Призма называется правильной, если ее основания являются правильными многоугольниками.
Площадью боковой поверхности призмы называется сумма площадей боковых граней.
Полная поверхность призмы равна сумме боковой поверхности и площадей оснований
Прямая призма. Свойства
Теорема Боковая поверхность прямой призмы равна произведению периметра основания на высоту призмы, т.е. на длину бокового ребра. Доказательство Боковые грани прямой призмы – прямоугольники. Основания этих прямоугольников являются сторонами многоугольника, лежащего в основании призмы, а высоты равны длине боковых ребер. Следовательно, боковая поверхность призмы равна  где a1, a2, …, an – длины ребер основания, p – периметр основания призмы, а l – длина боковых ребер. Теорема доказана. где a1, a2, …, an – длины ребер основания, p – периметр основания призмы, а l – длина боковых ребер. Теорема доказана.
| |
Параллелепипед
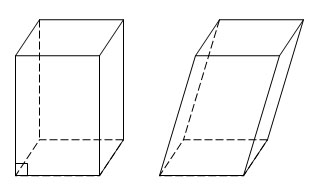 Параллелепипедом называется призма, в основании которой параллелограмм. Параллелепипед называется прямым, если его боковые ребра перпендикулярны основаниям. Параллелепипед называется наклонным, если его боковые ребра не перпендикулярны основаниям. Грани параллелепипеда, не имеющие общих вершин, называются противолежащими. Параллелепипедом называется призма, в основании которой параллелограмм. Параллелепипед называется прямым, если его боковые ребра перпендикулярны основаниям. Параллелепипед называется наклонным, если его боковые ребра не перпендикулярны основаниям. Грани параллелепипеда, не имеющие общих вершин, называются противолежащими.
| |
Параллелепипед. Свойства
Теорема У параллелепипеда противолежащие грани параллельны и равны.  Доказательство Возьмем любые две противолежащие грани параллелепипеда: A1A2A2`A1` и A3A4A4`A3`. Так как все грани параллелепипеда – параллелограммы, то прямая A1A2 параллельна прямой A4A3, а прямая A1A1` параллельна прямой A4A4`. Следовательно плоскости рассматриваемых граней параллельны. Так как грани параллелепипеда – параллелограммы, то отрезки A1A4, A1`A4`, A2`A3` и A2A3 – параллельны и равны. Следовательно грань A1A2A2`A1` совмещается параллельным переносом вдоль ребра A1A4 с гранью A3A4A4`A3` и, значит, грани равны. Точно также доказывается параллельность и равенство других противолежащих граней параллелепипеда. Теорема доказана. Доказательство Возьмем любые две противолежащие грани параллелепипеда: A1A2A2`A1` и A3A4A4`A3`. Так как все грани параллелепипеда – параллелограммы, то прямая A1A2 параллельна прямой A4A3, а прямая A1A1` параллельна прямой A4A4`. Следовательно плоскости рассматриваемых граней параллельны. Так как грани параллелепипеда – параллелограммы, то отрезки A1A4, A1`A4`, A2`A3` и A2A3 – параллельны и равны. Следовательно грань A1A2A2`A1` совмещается параллельным переносом вдоль ребра A1A4 с гранью A3A4A4`A3` и, значит, грани равны. Точно также доказывается параллельность и равенство других противолежащих граней параллелепипеда. Теорема доказана.
| |
Центральная симметрия параллелепипеда
Теорема Диагонали параллелепипеда пересекаются в одной точке и точкой пересечения делятся пополам.  Доказательство Рассмотрим любые две диагонали параллелепипеда, например A1A3` и A4A2`. Так как четырехугольники A1A2A3A4 и A2A2`A3`A3 – параллелограммы с общей стороной A2A3, то их стороны A1A4 и A2`A3` параллельны друг другу, следовательно, лежат в одной плоскости. Эта плоскость пересекает плоскости противолежащих граней параллелепипеда по параллельным прямым A1A2` и A4A3`. Следовательно, четырехугольник A4A1A2`A3` - параллелограмм. Диагонали параллелепипеда A1A3` и A2A4` являются диагоналями этого параллелограмма. Поэтому они пересекаются и точкой пересечения O делятся пополам. Аналогично доказывается, что диагонали A1A3` и A2A4`, а также диагонали A1A3` и A3A1` пересекаются и точкой пересечения делятся пополам. Теорема доказана. Доказательство Рассмотрим любые две диагонали параллелепипеда, например A1A3` и A4A2`. Так как четырехугольники A1A2A3A4 и A2A2`A3`A3 – параллелограммы с общей стороной A2A3, то их стороны A1A4 и A2`A3` параллельны друг другу, следовательно, лежат в одной плоскости. Эта плоскость пересекает плоскости противолежащих граней параллелепипеда по параллельным прямым A1A2` и A4A3`. Следовательно, четырехугольник A4A1A2`A3` - параллелограмм. Диагонали параллелепипеда A1A3` и A2A4` являются диагоналями этого параллелограмма. Поэтому они пересекаются и точкой пересечения O делятся пополам. Аналогично доказывается, что диагонали A1A3` и A2A4`, а также диагонали A1A3` и A3A1` пересекаются и точкой пересечения делятся пополам. Теорема доказана.
| |
Прямоугольный параллелепипед
 Прямоугольный параллелепипед, у которого основанием является прямоугольник, называется прямоугольным параллелепипедом. У прямоугольного параллелепипеда все грани – прямоугольники. Прямоугольный параллелепипед, у которого все ребра равны, называется кубом Длины непараллельных ребер прямоугольного параллелепипеда называются его линейными размерами. Прямоугольный параллелепипед, у которого основанием является прямоугольник, называется прямоугольным параллелепипедом. У прямоугольного параллелепипеда все грани – прямоугольники. Прямоугольный параллелепипед, у которого все ребра равны, называется кубом Длины непараллельных ребер прямоугольного параллелепипеда называются его линейными размерами.
| |
Прямоугольный параллелепипед. Свойство
Теорема В прямоугольном параллелепипеде квадрат любой диагонали равен сумме квадратов трех его измерений. Доказательство Рассмотрим прямоугольный параллелепипед ABCDA`B`C`D`. По теореме Пифагора в треугольнике AC`C получаем: 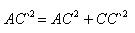 Из прямоугольного треугольника ACB по теореме Пифагора получаем Из прямоугольного треугольника ACB по теореме Пифагора получаем  Ребра AB, BC и CC` не параллельны, а следовательно, их длины являются линейными размерами параллелепипеда. Теорема доказана. Ребра AB, BC и CC` не параллельны, а следовательно, их длины являются линейными размерами параллелепипеда. Теорема доказана.
| |
Пирамида
 Пирамидой называется многогранник, который состоит из плоского многоугольника – основания пирамиды, точки, не лежащей в плоскости основания, - вершины пирамиды и всех отрезков, соединяющих вершину пирамиды с точками основания. Отрезки, соединяющие вершину пирамиды с вершинами основания, называются боковыми ребрами. A1A2A34 – основание пирамиды, S – вершина пирамиды, A1S, A2S, A3S, A4S – ребра пирамиды. Высотой пирамиды называется перпендикуляр, опущенный из вершины пирамиды на плоскость основания. Пирамидой называется многогранник, который состоит из плоского многоугольника – основания пирамиды, точки, не лежащей в плоскости основания, - вершины пирамиды и всех отрезков, соединяющих вершину пирамиды с точками основания. Отрезки, соединяющие вершину пирамиды с вершинами основания, называются боковыми ребрами. A1A2A34 – основание пирамиды, S – вершина пирамиды, A1S, A2S, A3S, A4S – ребра пирамиды. Высотой пирамиды называется перпендикуляр, опущенный из вершины пирамиды на плоскость основания.
| | | | | | |
| |
Усеченная пирамида
Теорема
Плоскость, пересекающая пирамиду и параллельная ее основанию, отсекает подобную пирамиду.

Доказательство
Пусть S – вершина пирамиды, A – вершина основания и A` - точка пересечения секущей плоскости с боковым ребром SA. Подвергнем пирамиду преобразованию гомотетии относительно вершины S с коэффициентом гомотетии

При этой гомотетии плоскость основания переходит в параллельную плоскость, проходящую через точку A`, т.е. в секущую плоскость, а следовательно, вся пирамида - в отсекаемую этой плоскость часть. Так как гомотетия есть преобразование подобия, то отсекаемая часть пирамиды является пирамидой, подобной данной. Теорема доказана.
| Правильная пирамида
Пирамида называется правильной, если ее основанием является правильный многоугольник, а высоты совпадают с центром этого многоугольника. Осью правильного пирамиды называется прямая, содержащая высоту. У правильной пирамиды: 1. Боковы ребра равны; 2. Боковые грани – равнобедренные треугольники. Высота боковой грани правильной пирамиды, проведенная из ее вершины, называется апофемой.
| |
Правильная пирамида. Свойства
Боковой поверхностью пирамиды называется сумма площадей ее боковых граней. Теорема Боковая поверхность правильной пирамиды равна произведению полупериметра основания на апофему.  Доказательство Если сторона основания a, число сторон n, то боковая поверхность пирамиды равна: Доказательство Если сторона основания a, число сторон n, то боковая поверхность пирамиды равна:  где l – апофема, p – периметр основания пирамиды. Теорема доказана. где l – апофема, p – периметр основания пирамиды. Теорема доказана.
| |
Правильные многогранники
Выпуклый многогранник называется правильным, если его грани являются правильными многоугольниками с один и тем же числом сторон и в каждой вершине многогранника сходится одно и то же число ребер.

У тетраэдра грани – правильные треугольники. В каждой вершине сходится по три ребра. Тетраэдр представляет собой треугольную пирамиду, у которой все ребра равны.
У куба все грани – квадраты. В каждой вершине сходятся по три ребра. Куб – это прямоугольный параллелепипед с равными ребрами.
У октаэдра грани – правильные треугольники. В каждой вершине сходится по четыре ребра.
У додекаэдра грани – правильные пятиугольники. В каждой вершине сходится по три ребра.
У икосаэдра грани – правильные треугольники. В каждой точке сходится по пять ребер.





 Свойства призмы: 1. Основания призмы равны и лежат в параллельных плоскостях. 2. Боковые ребра параллельны и равны. Поверхность призмы состоит из оснований и боковой поверхности. Боковая поверхность состоит из параллелограммов. Высотой призмы называется расстояние между плоскостями. Отрезок, соединяющий две вершины призмы, не принадлежащие одной грани, называется диагональю призмы.
Свойства призмы: 1. Основания призмы равны и лежат в параллельных плоскостях. 2. Боковые ребра параллельны и равны. Поверхность призмы состоит из оснований и боковой поверхности. Боковая поверхность состоит из параллелограммов. Высотой призмы называется расстояние между плоскостями. Отрезок, соединяющий две вершины призмы, не принадлежащие одной грани, называется диагональю призмы.
 где a1, a2, …, an – длины ребер основания, p – периметр основания призмы, а l – длина боковых ребер. Теорема доказана.
где a1, a2, …, an – длины ребер основания, p – периметр основания призмы, а l – длина боковых ребер. Теорема доказана.
 Параллелепипедом называется призма, в основании которой параллелограмм. Параллелепипед называется прямым, если его боковые ребра перпендикулярны основаниям. Параллелепипед называется наклонным, если его боковые ребра не перпендикулярны основаниям. Грани параллелепипеда, не имеющие общих вершин, называются противолежащими.
Параллелепипедом называется призма, в основании которой параллелограмм. Параллелепипед называется прямым, если его боковые ребра перпендикулярны основаниям. Параллелепипед называется наклонным, если его боковые ребра не перпендикулярны основаниям. Грани параллелепипеда, не имеющие общих вершин, называются противолежащими.
 Доказательство Возьмем любые две противолежащие грани параллелепипеда: A1A2A2`A1` и A3A4A4`A3`. Так как все грани параллелепипеда – параллелограммы, то прямая A1A2 параллельна прямой A4A3, а прямая A1A1` параллельна прямой A4A4`. Следовательно плоскости рассматриваемых граней параллельны. Так как грани параллелепипеда – параллелограммы, то отрезки A1A4, A1`A4`, A2`A3` и A2A3 – параллельны и равны. Следовательно грань A1A2A2`A1` совмещается параллельным переносом вдоль ребра A1A4 с гранью A3A4A4`A3` и, значит, грани равны. Точно также доказывается параллельность и равенство других противолежащих граней параллелепипеда. Теорема доказана.
Доказательство Возьмем любые две противолежащие грани параллелепипеда: A1A2A2`A1` и A3A4A4`A3`. Так как все грани параллелепипеда – параллелограммы, то прямая A1A2 параллельна прямой A4A3, а прямая A1A1` параллельна прямой A4A4`. Следовательно плоскости рассматриваемых граней параллельны. Так как грани параллелепипеда – параллелограммы, то отрезки A1A4, A1`A4`, A2`A3` и A2A3 – параллельны и равны. Следовательно грань A1A2A2`A1` совмещается параллельным переносом вдоль ребра A1A4 с гранью A3A4A4`A3` и, значит, грани равны. Точно также доказывается параллельность и равенство других противолежащих граней параллелепипеда. Теорема доказана.
 Доказательство Рассмотрим любые две диагонали параллелепипеда, например A1A3` и A4A2`. Так как четырехугольники A1A2A3A4 и A2A2`A3`A3 – параллелограммы с общей стороной A2A3, то их стороны A1A4 и A2`A3` параллельны друг другу, следовательно, лежат в одной плоскости. Эта плоскость пересекает плоскости противолежащих граней параллелепипеда по параллельным прямым A1A2` и A4A3`. Следовательно, четырехугольник A4A1A2`A3` - параллелограмм. Диагонали параллелепипеда A1A3` и A2A4` являются диагоналями этого параллелограмма. Поэтому они пересекаются и точкой пересечения O делятся пополам. Аналогично доказывается, что диагонали A1A3` и A2A4`, а также диагонали A1A3` и A3A1` пересекаются и точкой пересечения делятся пополам. Теорема доказана.
Доказательство Рассмотрим любые две диагонали параллелепипеда, например A1A3` и A4A2`. Так как четырехугольники A1A2A3A4 и A2A2`A3`A3 – параллелограммы с общей стороной A2A3, то их стороны A1A4 и A2`A3` параллельны друг другу, следовательно, лежат в одной плоскости. Эта плоскость пересекает плоскости противолежащих граней параллелепипеда по параллельным прямым A1A2` и A4A3`. Следовательно, четырехугольник A4A1A2`A3` - параллелограмм. Диагонали параллелепипеда A1A3` и A2A4` являются диагоналями этого параллелограмма. Поэтому они пересекаются и точкой пересечения O делятся пополам. Аналогично доказывается, что диагонали A1A3` и A2A4`, а также диагонали A1A3` и A3A1` пересекаются и точкой пересечения делятся пополам. Теорема доказана.
 Прямоугольный параллелепипед, у которого основанием является прямоугольник, называется прямоугольным параллелепипедом. У прямоугольного параллелепипеда все грани – прямоугольники. Прямоугольный параллелепипед, у которого все ребра равны, называется кубом Длины непараллельных ребер прямоугольного параллелепипеда называются его линейными размерами.
Прямоугольный параллелепипед, у которого основанием является прямоугольник, называется прямоугольным параллелепипедом. У прямоугольного параллелепипеда все грани – прямоугольники. Прямоугольный параллелепипед, у которого все ребра равны, называется кубом Длины непараллельных ребер прямоугольного параллелепипеда называются его линейными размерами.
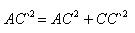 Из прямоугольного треугольника ACB по теореме Пифагора получаем
Из прямоугольного треугольника ACB по теореме Пифагора получаем  Ребра AB, BC и CC` не параллельны, а следовательно, их длины являются линейными размерами параллелепипеда. Теорема доказана.
Ребра AB, BC и CC` не параллельны, а следовательно, их длины являются линейными размерами параллелепипеда. Теорема доказана.
 Пирамидой называется многогранник, который состоит из плоского многоугольника – основания пирамиды, точки, не лежащей в плоскости основания, - вершины пирамиды и всех отрезков, соединяющих вершину пирамиды с точками основания. Отрезки, соединяющие вершину пирамиды с вершинами основания, называются боковыми ребрами. A1A2A34 – основание пирамиды, S – вершина пирамиды, A1S, A2S, A3S, A4S – ребра пирамиды. Высотой пирамиды называется перпендикуляр, опущенный из вершины пирамиды на плоскость основания.
Пирамидой называется многогранник, который состоит из плоского многоугольника – основания пирамиды, точки, не лежащей в плоскости основания, - вершины пирамиды и всех отрезков, соединяющих вершину пирамиды с точками основания. Отрезки, соединяющие вершину пирамиды с вершинами основания, называются боковыми ребрами. A1A2A34 – основание пирамиды, S – вершина пирамиды, A1S, A2S, A3S, A4S – ребра пирамиды. Высотой пирамиды называется перпендикуляр, опущенный из вершины пирамиды на плоскость основания.
 Доказательство Если сторона основания a, число сторон n, то боковая поверхность пирамиды равна:
Доказательство Если сторона основания a, число сторон n, то боковая поверхность пирамиды равна:  где l – апофема, p – периметр основания пирамиды. Теорема доказана.
где l – апофема, p – периметр основания пирамиды. Теорема доказана.