Переходим к комплексной передаточной функции
p→jω
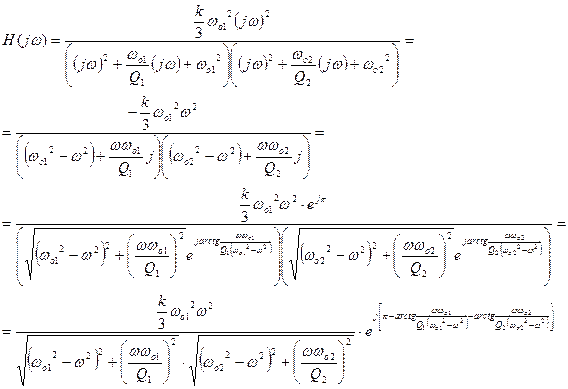
Отсюда находим АЧХ
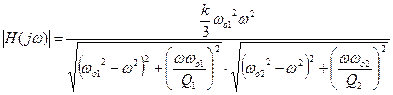
Где
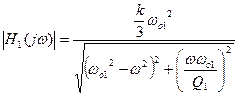
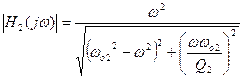
находим ФЧХ
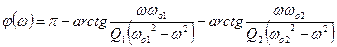
где
Подставляем числовые значения
R1 = 100 кОм = 105 Ом
R2 = 68 кОм = 0,68×105 Ом
R3 = 116 кОм = 1,16×105 Ом
С1 = 2,4 нФ = 2,4×10-9 Ф
С2 = 1 нФ = 10-9 Ф
К = 3,2
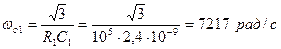
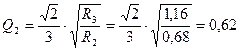
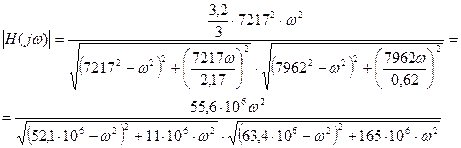
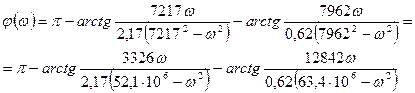
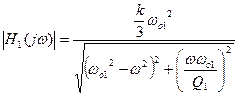
При ω =0
Н1(0) =k/3
При ω = ωo1
Н1(ωo1) =Q1k/3=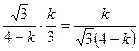 
При ω = ∞
Н1(∞) = 0
Таким образом, первое звено фильтра является ФНЧ
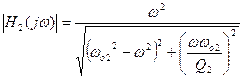
При ω =0
Н2(0) = 0
При ω = ωo2
Н2(ωo2) = Q2 =0,62
При ω = ∞
Н2(∞) = 1
Таким образом, второе звено фильтра является ФВЧ
Таблица 1. Значения АЧХ и ФЧХ первого и второго звена и фильтра в целом.
| ω, рад/с | IН1(jω)I | IН2(jω)I | IН(jω)I | φ1(ω), рад | φ2(ω), рад | φ(ω), рад |
| 1,067 | 0,000 | 0,000 | 0,000 | 3,142 | 3,142 | |
| 1,071 | 0,004 | 0,004 | -0,032 | 3,040 | 3,007 | |
| 1,085 | 0,016 | 0,017 | -0,065 | 2,937 | 2,872 | |
| 1,109 | 0,035 | 0,039 | -0,100 | 2,834 | 2,734 | |
| 1,144 | 0,062 | 0,071 | -0,138 | 2,731 | 2,593 | |
| 1,193 | 0,095 | 0,114 | -0,180 | 2,627 | 2,447 | |
| 1,256 | 0,135 | 0,169 | -0,228 | 2,522 | 2,294 | |
| 1,338 | 0,179 | 0,240 | -0,285 | 2,417 | 2,132 | |
| 1,444 | 0,228 | 0,329 | -0,354 | 2,312 | 1,959 | |
| 1,579 | 0,280 | 0,441 | -0,440 | 2,209 | 1,768 | |
| 1,747 | 0,332 | 0,581 | -0,552 | 2,107 | 1,555 | |
| 1,949 | 0,386 | 0,751 | -0,698 | 2,007 | 1,308 | |
| 2,165 | 0,438 | 0,947 | -0,894 | 1,910 | 1,017 | |
| 2,335 | 0,487 | 1,138 | -1,145 | 1,817 | 0,672 | |
| 2,360 | 0,535 | 1,262 | -1,439 | 1,728 | 0,289 | |
| 2,192 | 0,578 | 1,268 | -1,736 | 1,644 | -0,092 | |
| 1,902 | 0,619 | 1,177 | -1,991 | 1,565 | -0,426 | |
| 1,597 | 0,655 | 1,047 | -2,189 | 1,490 | -0,699 | |
| 1,333 | 0,688 | 0,918 | -2,338 | 1,421 | -0,917 | |
| 1,120 | 0,718 | 0,804 | -2,449 | 1,356 | -1,093 | |
| 0,952 | 0,744 | 0,708 | -2,534 | 1,295 | -1,239 | |
| 0,818 | 0,768 | 0,628 | -2,600 | 1,238 | -1,361 | |
| 0,712 | 0,788 | 0,561 | -2,653 | 1,186 | -1,467 | |
| 0,625 | 0,807 | 0,505 | -2,696 | 1,137 | -1,558 | |
| 0,554 | 0,824 | 0,456 | -2,731 | 1,092 | -1,639 | |
| 0,495 | 0,838 | 0,415 | -2,761 | 1,049 | -1,712 | |
| 0,446 | 0,851 | 0,379 | -2,787 | 1,010 | -1,777 | |
| 0,403 | 0,863 | 0,348 | -2,809 | 0,973 | -1,836 | |
| 0,367 | 0,873 | 0,321 | -2,828 | 0,939 | -1,889 | |
| 0,336 | 0,883 | 0,297 | -2,845 | 0,906 | -1,939 | |
| 0,309 | 0,891 | 0,275 | -2,860 | 0,876 | -1,984 | |
| 0,285 | 0,899 | 0,256 | -2,874 | 0,848 | -2,026 | |
| 0,264 | 0,906 | 0,239 | -2,886 | 0,821 | -2,065 | |
| 0,245 | 0,912 | 0,223 | -2,897 | 0,796 | -2,101 | |
| 0,228 | 0,917 | 0,209 | -2,907 | 0,772 | -2,134 | |
| 0,213 | 0,923 | 0,197 | -2,916 | 0,750 | -2,166 | |
| 0,200 | 0,927 | 0,185 | -2,924 | 0,729 | -2,195 | |
| 0,187 | 0,932 | 0,174 | -2,932 | 0,709 | -2,223 |
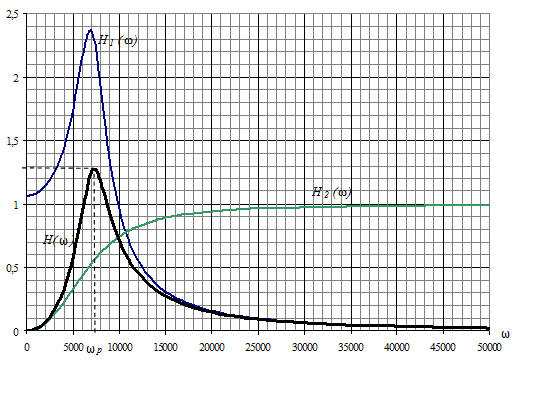
Рис.6. График АЧХ фильтра
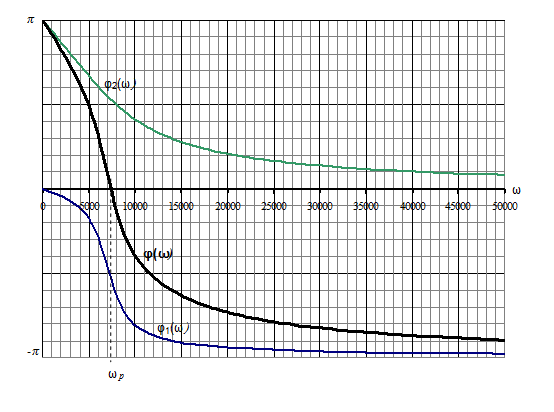
Рис.7. График ФЧХ фильтра
В соответствие с построенной АЧХ фильтра тип фильтра определяется как полосовой (ПФ)
Найти переходную характеристику первого звена фильтра и построить ее график
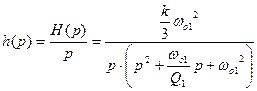
Раскладываем рациональную дробь на слагаемые
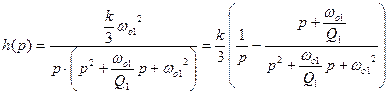
Изображение первого слагаемого по Лапласу – единичный скачок.
Чтобы найти обратное изображение второго слагаемого воспользуемся теоремой о разложении
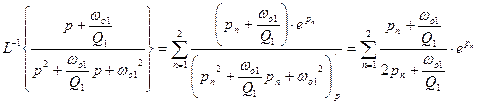
Найдем корни характеристического многочлена рn
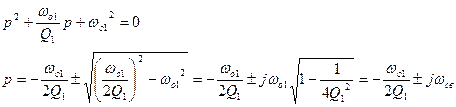
Где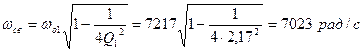 
- круговая частота свободных колебаний первого звена
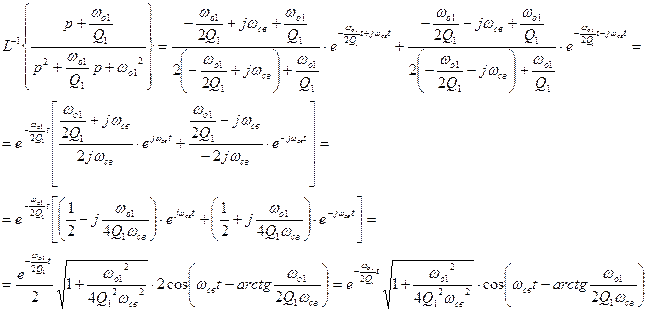
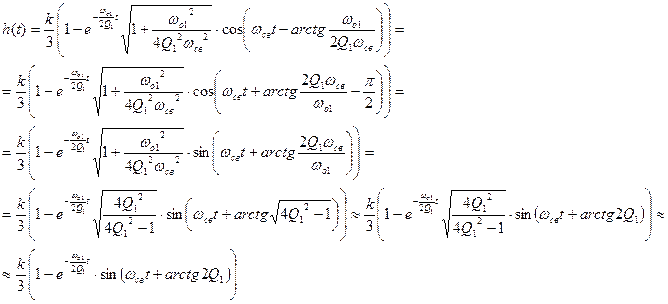Подставляя числовые значения, получаем:
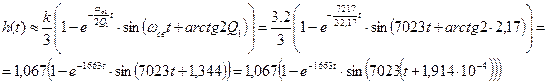
При измерении времени в миллисекундах
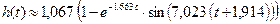
Период свободных колебаний
Таблица 2
| t,мс | h(t), B |
| 0,247586 | |
| 0,25 | 0,723179 |
| 0,5 | 1,507212 |
| 0,75 | 1,109862 |
| 0,864931 | |
| 1,25 | 1,097379 |
| 1,5 | 1,147607 |
| 1,75 | 1,034211 |
| 1,039862 | |
| 2,25 | 1,087863 |
| 2,5 | 1,073753 |
| 2,75 | 1,056278 |
| 1,066662 | |
| 3,25 | 1,07175 |
| 3,5 | 1,065994 |
| 3,75 | 1,065176 |
| 1,067881 | |
| 4,25 | 1,067581 |
| 4,5 | 1,066476 |
| 4,75 | 1,066874 |
| 1,067259 |
Рис.8. График переходной характеристики первого звена фильтра
Оценить допустимую величину ступенчатого воздействия на фильтр, если напряжение на входе усилителя второго звена фильтра во избежание его перегрузки не должно превышать 0,2 В.
максимальное значение сигнала
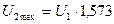
Тогда допустимое значение амплитуды ступенчатого воздействия равно
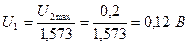
5. Получить выражения и построить графики:
Спектральной плотности амплитуд
Спектра фаз
Спектральной плотности энергии колебаний на входе фильтра, если к его входу подведен одиночный импульс заданной формы. Оценить области концентрации энергии воздействия и реакции, показать на графике ширину спектра
Входным импульсом является видеоимпульс
Рис.9. Видеоимпульс прямоугольной формы
высота импульса,
u(t) = U
где U= 0,9∙Uдоп. = 0,9×0,12 = 0,11В
Длительность импульса
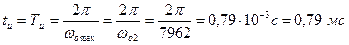
Находим комплексную спектральную плотность
5.1 Спектральная плотность амплитуд будет равна модулю комплексной спектральной плотности
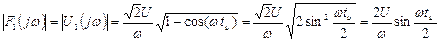
5.2 Спектр фаз будет равен аргументу комплексной спектральной плотности
5.3 Спектральная плотность энергии входного сигнала
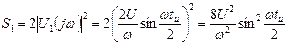
На выходе фильтра спектральная плотность амплитуд
Спектр фаз
Спектральная плотность энергии-+
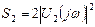
Таблица 3. результаты расчета спектральной плотности амплитуд, спектра фаз и спектральной плотности энергии
| ω, рад/с | U1(ω), мкВ×с | φ1(ω), рад | S1, мкВ2×с2 | Н(ω) | φ(ω), рад | U2(ω), мкВ×с | φ2(ω), рад | S2, мкВ2×с2 |
| 3,142 | 3,142 | |||||||
| 24,02507192 | -0,1975 | 1154,408161 | 0,004 | 3,007 | 0,096100288 | 2,8095 | 0,018470531 | |
| 46,20013076 | -0,395 | 4268,904164 | 0,017 | 2,872 | 0,785402223 | 2,477 | 1,233713303 | |
| 64,86510659 | -0,5925 | 8414,964106 | 0,039 | 2,734 | 2,529739157 | 2,1415 | 12,79916041 | |
| 78,71787637 | -0,79 | 12393,00812 | 0,071 | 2,593 | 5,588969223 | 1,803 | 62,47315394 | |
| 86,94109193 | -0,9875 | 15117,50693 | 0,114 | 2,447 | 9,91128448 | 1,4595 | 196,4671201 | |
| 89,27365498 | -1,185 | 15939,57095 | 0,169 | 2,294 | 15,08724769 | 1,109 | 455,2500858 | |
| 86,01942946 | -1,3825 | 14798,68449 | 0,24 | 2,132 | 20,64466307 | 0,7495 | 852,4042265 | |
| 77,99339299 | -1,58 | 12165,9387 | 0,329 | 1,959 | 25,65982629 | 0,379 | 1316,853371 | |
| 66,41291979 | -1,7775 | 8821,351829 | 0,441 | 1,768 | 29,28809763 | -0,0095 | 1715,585325 | |
| 52,74831421 | -1,975 | 5564,769305 | 0,581 | 1,555 | 30,64677056 | -0,42 | 1878,449091 | |
| 38,55128379 | -2,1725 | 2972,402963 | 0,751 | 1,308 | 28,95201412 | -0,8645 | 1676,438244 | |
| 25,2822047 | -2,37 | 1278,379749 | 0,947 | 1,017 | 23,94224785 | -1,353 | 1146,462465 | |
| 14,15656431 | -2,5675 | 400,8166264 | 1,138 | 0,672 | 16,11017019 | -1,8955 | 519,0751671 | |
| 6,027975234 | -2,765 | 72,67297085 | 1,262 | 0,289 | 7,607304746 | -2,476 | 115,742171 | |
| 1,320081322 | -2,9625 | 3,485229392 | 1,268 | -0,092 | 1,673863116 | -3,0545 | 5,603635461 | |
| 0,013212893 | -3,16 | 0,000349161 | 1,177 | -0,426 | 0,015551575 | -3,586 | 0,000483703 | |
| 1,684657563 | -3,3575 | 5,676142211 | 1,047 | -0,699 | 1,763836469 | -4,0565 | 6,222238177 | |
| 5,594803578 | -3,555 | 62,60365416 | 0,918 | -0,917 | 5,136029685 | -4,472 | 52,75760185 | |
| 10,8060214 | -3,7525 | 233,5401969 | 0,804 | -1,093 | 8,688041205 | -4,8455 | 150,9641199 | |
| 16,31763316 | -3,95 | 532,5303039 | 0,708 | -1,239 | 11,55288428 | -5,189 | 266,9382702 | |
| 21,19907196 | -4,1475 | 898,8013036 | 0,628 | -1,361 | 13,31301719 | -5,5085 | 354,4728533 | |
| 24,70443841 | -4,345 | 1220,618555 | 0,561 | -1,467 | 13,85918995 | -5,812 | 384,1542922 | |
| 26,35489353 | -4,5425 | 1389,160826 | 0,505 | -1,558 | 13,30922123 | -6,1005 | 354,2707396 | |
| 25,98018346 | -4,74 | 1349,939865 | 0,456 | -1,639 | 11,84696366 | -6,379 | 280,7010958 | |
| 23,71637425 | -4,9375 | 1124,932815 | 0,415 | -1,712 | 9,842295313 | -6,6495 | 193,7415541 | |
| 19,96278225 | -5,135 | 797,02535 | 0,379 | -1,777 | 7,565894471 | -6,912 | 114,4855183 | |
| 15,30633029 | -5,3325 | 468,567494 | 0,348 | -1,836 | 5,326602942 | -7,1685 | 56,7453978 | |
| 10,42546715 | -5,53 | 217,3807305 | 0,321 | -1,889 | 3,346574955 | -7,419 | 22,39912785 | |
| 5,987888486 | -5,7275 | 71,70961705 | 0,297 | -1,939 | 1,77840288 | -7,6665 | 6,32543361 | |
| 2,556383091 | -5,925 | 13,07018901 | 0,275 | -1,984 | 0,70300535 | -7,909 | 0,988433044 | |
| 0,515269236 | -6,1225 | 0,531004772 | 0,256 | -2,026 | 0,131908924 | -8,1485 | 0,034799929 | |
| 0,026416834 | -6,32 | 0,001395698 | 0,239 | -2,065 | 0,006313623 | -8,385 | 7,97237E-05 | |
| 1,019311724 | -6,5175 | 2,077992783 | 0,223 | -2,101 | 0,227306515 | -8,6185 | 0,103336503 | |
| 3,214676637 | -6,715 | 20,66829176 | 0,209 | -2,134 | 0,671867417 | -8,849 | 0,902811652 | |
| 6,176516296 | -6,9125 | 76,2987071 | 0,197 | -2,166 | 1,21677371 | -9,0785 | 2,961076524 | |
| 9,383732517 | -7,11 | 176,1088719 | 0,185 | -2,195 | 1,735990516 | -9,305 | 6,027326141 | |
| 12,31013731 | -7,3075 | 303,0789612 | 0,174 | -2,223 | 2,141963892 | -9,5305 | 9,176018628 | |
| 14,50104321 | -7,505 | 420,5605084 | 0,165 | -2,249 | 2,39267213 | -9,754 | 11,44975984 | |
| 15,63565272 | -7,7025 | 488,9472722 | 0,156 | -2,274 | 2,439161825 | -9,9765 | 11,89902082 | |
| 15,56698735 | -7,9 | 484,6621903 | 0,148 | -2,297 | 2,303914128 | -10,197 | 10,61604062 | |
| 14,33467695 | -8,0975 | 410,9659264 | 0,14 | -2,319 | 2,006854773 | -10,4165 | 8,054932158 | |
| 12,15002312 | -8,295 | 295,2461236 | 0,133 | -2,34 | 1,615953075 | -10,635 | 5,22260868 | |
| 9,356755232 | -8,4925 | 175,0977369 | 0,127 | -2,36 | 1,188307914 | -10,8525 | 2,824151399 | |
| 6,374248297 | -8,69 | 81,26208269 | 0,121 | -2,379 | 0,771284044 | -11,069 | 1,189758153 | |
| 3,63221523 | -8,8875 | 26,38597495 | 0,115 | -2,397 | 0,417704751 | -11,2845 | 0,348954519 | |
| 1,506743801 | -9,085 | 4,540553763 | 0,11 | -2,414 | 0,165741818 | -11,499 | 0,054940701 | |
| 0,266949762 | -9,2825 | 0,142524351 | 0,105 | -2,43 | 0,028029725 | -11,7125 | 0,001571331 | |
| 0,039602876 | -9,48 | 0,003136776 | 0,101 | -2,446 | 0,003999891 | -11,926 | 3,19982E-05 | |
| 0,796175992 | -9,6775 | 1,267792421 | 0,097 | -2,461 | 0,077229071 | -12,1385 | 0,011928659 | |
| 2,363324818 | -9,875 | 11,17060839 | 0,093 | -2,475 | 0,219789208 | -12,35 | 0,096614592 | |
| 4,454344882 | -10,0725 | 39,68237665 | 0,089 | -2,489 | 0,396436694 | -12,5615 | 0,314324105 | |
| 6,716174908 | -10,27 | 90,21401079 | 0,085 | -2,502 | 0,570874867 | -12,772 | 0,651796228 | |
| 8,784438055 | -10,4675 | 154,3327039 | 0,082 | -2,514 | 0,720323921 | -12,9815 | 1,037733101 | |
| 10,33810555 | -10,665 | 213,7528529 | 0,079 | -2,526 | 0,816710339 | -13,191 | 1,334031555 | |
| 11,14572373 | -10,8625 | 248,4543149 | 0,076 | -2,538 | 0,847075003 | -13,4005 | 1,435072123 | |
| 11,09667075 | -11,06 | 246,2722034 | 0,073 | -2,549 | 0,810056965 | -13,609 | 1,312384572 | |
| 10,21334218 | -11,2575 | 208,6247168 | 0,071 | -2,56 | 0,725147295 | -13,8175 | 1,051677198 | |
| 8,643118488 | -11,455 | 149,4069944 | 0,068 | -2,57 | 0,587732057 | -14,025 | 0,690857942 | |
| 6,631993313 | -11,6525 | 87,9666706 | 0,066 | -2,58 | 0,437711559 | -14,2325 | 0,383182817 | |
| 4,48439171 | -11,85 | 40,21953801 | 0,064 | -2,59 | 0,287001069 | -14,44 | 0,164739228 |
Рис.10. Спектральная плотность амплитуд
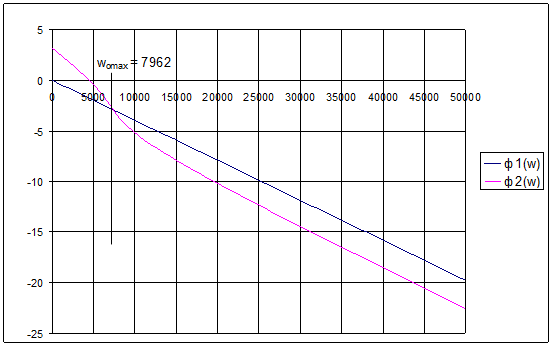
Рис.11. Спектр фаз
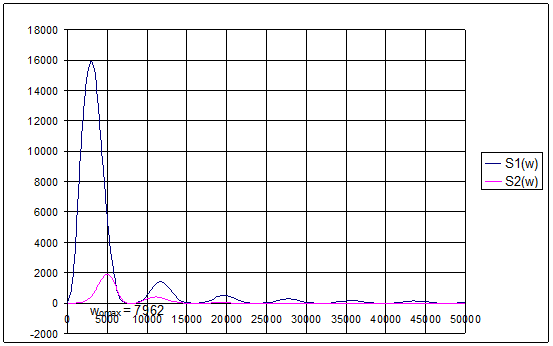
Рис.10. Спектральная плотность энергии
Убедиться в устойчивости фильтра по расположению полюсов его передаточной функции, показав их на комплексной плоскости
Характеристический многочлен 4 степени. Передаточная функция имеет 4 полюса
Найдем полюса передаточной функции
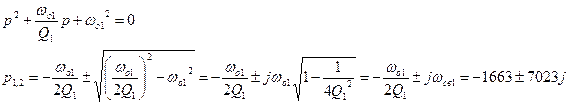
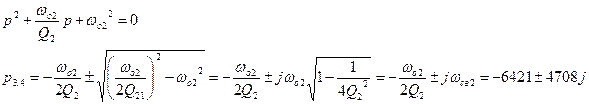
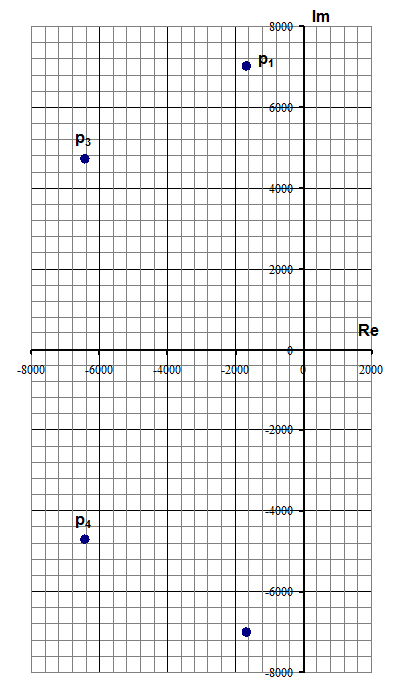
Рис. 13. Полюса передаточной функции
Все корни находятся в левой полуплоскости комплексной плоскости – следовательно, фильтр устойчивая система
Построить годограф передаточной функции по петле обратной связи первого звена фильтра, разомкнув цепь обратной связи на входе первого усилителя звена. Убедится в устойчивости фильтра по критерию Найквиста.
Составляем разомкнутую схему
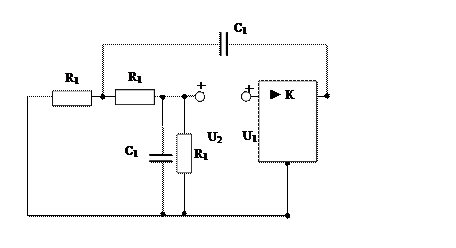
Рис.14. Первое звено фильтра
Схема замещения
Рис.15. Схема замещения
Составляем узловые уравнения для второго и третьего узлов
| Y22 | -Y23 | × | U2 | = | Y24U2 |
| -Y32 | Y33 | U3 | Y34U3 |
| 
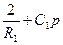
| × | U2 | = | |
|
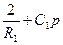
| U3 | 
|
|
|
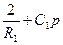
| × | U2/U1 | = | |
|
|
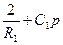
| U3/U1 |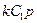 
|
|
|
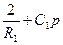
| × | B12(p) | = | |
|
|
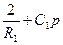
| B13(p) |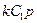
|
| 
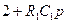
| × | B12(p) | = | |
|
|
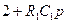
| B13(p) |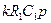 
|
|
| |
|
|
| |
|
|
| |
|
|
|
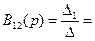
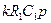
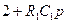
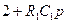
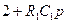
Таким образом, получаем передаточную функцию по петле обратной связи
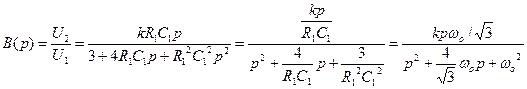
где формальная резонансная частота
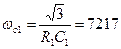
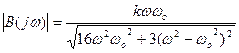
Строим годограф при изменении частоты от 0 до ∞
| ω, рад/с | IВ(jω)I | φ(ω), рад |
| 1,571 | ||
| 0,127 | 1,411 | |
| 0,248 | 1,255 | |
| 0,359 | 1,106 | |
| 0,456 | 0,965 | |
| 0,538 | 0,833 | |
| 0,606 | 0,711 | |
| 0,661 | 0,599 | |
| 0,704 | 0,496 | |
| 0,736 | 0,401 | |
| 0,761 | 0,314 | |
| 0,778 | 0,234 | |
| 0,790 | 0,159 | |
| 0,797 | 0,091 | |
| 0,800 | 0,026 | |
| 0,8 | 0,000 | |
| 0,797 | -0,089 | |
| 0,786 | -0,190 | |
| 0,769 | -0,280 | |
| 0,749 | -0,360 | |
| 0,727 | -0,431 | |
| 0,704 | -0,495 | |
| 0,681 | -0,553 | |
| 0,658 | -0,605 | |
| 0,635 | -0,653 | |
| 0,614 | -0,696 | |
| 0,593 | -0,736 | |
| 0,573 | -0,773 | |
| 0,553 | -0,807 | |
| 0,471 | -0,942 | |
| 0,406 | -1,038 | |
| 0,356 | -1,109 | |
| 0,316 | -1,164 | |
| 0,284 | -1,208 | |
| 0,258 | -1,243 | |
| 0,236 | -1,272 | |
| 0,217 | -1,296 | |
| 0,201 | -1,317 | |
| 0,187 | -1,335 | |
| 0,175 | -1,350 | |
| 0,164 | -1,364 | |
| 0,155 | -1,376 | |
| 0,147 | -1,387 | |
| 0,139 | -1,396 | |
| 0,132 | -1,405 | |
| 0,126 | -1,413 | |
| 0,120 | -1,420 | |
| 0,115 | -1,426 | |
| 0,110 | -1,432 | |
| 0,106 | -1,438 | |
| 0,102 | -1,443 | |
| 0,098 | -1,448 | |
| 0,095 | -1,452 | |
| 0,092 | -1,456 | |
| 0,089 | -1,460 | |
| ∞ | -1,571 |
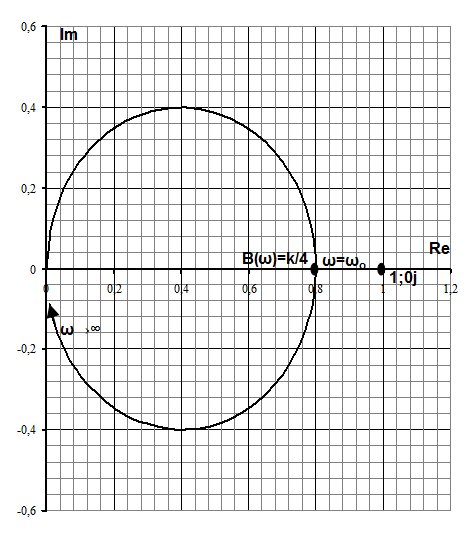
Рис. 16. Годограф передаточной функции по петле обратной связи
При возрастании частоты от 0 до ∞ годограф не охватывает точку (1;0j) – следовательно, согласно критерию Найквиста звено устойчиво.
При каких значения коэффициента усиления усилителя первого звена фильтра, цепь будет находиться строго на границе устойчивости. Чему при этом равна частота свободных колебаний в каскаде?
При k/4 =1 звено находится на границе устойчивости, при этом k = 4.
При этом добротность становится бесконечно большой
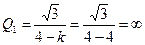
Частота свободных колебаний становится равной резонансной
