Определение времени и пути разгона машины, оборудованной коробкой передач с переключением без разрыва потока мощности
Коробки передач с переключением передач без разрыва потока мощности (КПБРМ) получают известное распространение на сельскохозяйственных тракторах, которые имеют большое количество передач для обеспечения различных технологических процессов. Однако целесообразность их применения на быстроходных гусеничных машинах (БГМ), у которых количество передач ограничено, не очевидна из-за большей сложности и стоимости, а также дополнительных потерь мощности сравнительно с широко применяемыми более простыми механическими КП. Для БГМ, а также автомобилей, имеющих количество передач свыше пяти, преимущества переключения передач без разрыва потока мощности могут перевешивать их недостатки, указанные выше. Для армейских ГМ, используемых в военных условиях, время и путь разгона могут иметь решающее значение. В работе проведена сравнительная оценка БГМ, оборудованной пятискоростной механической синхронизированной КП и КПБРМ, которая показала преимущества переключения передач без разрыва потока мощности в снижении времени и пути разгона соответственно в 1,3 и 1,2 раза. Для выполнения расчетов была разработана методика и алгоритм точного расчета параметров разгона машины в сравнении с широко используемым на практике приближенным методом графоаналитического интегрирования проф. Н.А. Яковлева. Методика точного расчета базируется на решении дифференциального уравнения, связывающего ускорение с параметрами разгона ГМ при начальных условиях, соответствующим началу ее движения. Методика и алгоритм расчета могут быть использованы также для определения тягово-скоростных и топливно - экономических качеств других транспортных средств, в том числе, автомобилей.
Введение
Коробки передач (КП) с переключением передач без разрыва потока мощности (КПБРМ) или КП с переключением без остановки машины получают известное распространение на сельскохозяйственных тракторах. Не так очевидна целесообразность установки КПБРМ на транспортно-тяговые быстроходные гусеничные машины (БГМ). Преимуществом КПБРМ является поддержание непрерывности технологического процесса, повышение производительности сельскохозяйственных МТА и сокращение времени и пути разгона для БГМ. Если это преимущество КПБРМ для МТА было подтверждено на практике, то для БГМ можно только предполагать о такой возможности.
Действительно, каждое переключение передачи сопровождается снижением скорости машины, тем большим, чем длительнее процесс переключения, что и приводит к увеличению времени и пути разгона машины. Для гусеничных машин эффект снижения скорости должен быть значительнее, чем для колесных, у которых сохраняется движение за счет наката. Экспериментальные данные о влиянии КПБРМ на время и путь разгона БГМ отсутствуют. Не разработана также методика определения времени и пути разгона машин, оборудованных КПБРМ. При определении тягово-скоростных показателей автомобилей, колесных и гусеничных машин, оборудованных механической КП, обычно используют приближенный метод графо-аналитического интегрирования проф. Н.А.Яковлева. [1-4].
В данной работе предлагается методика точного расчета времени и пути разгона БГМ, оборудованной КПБРМ, на основе решения дифференциального уравнения  при начальных условиях t=0, v=0. По методике проводится сравнение показателей разгона БГМ, оборудованной механической ступенчатой синхронизированной КП и КПБРМ.
при начальных условиях t=0, v=0. По методике проводится сравнение показателей разгона БГМ, оборудованной механической ступенчатой синхронизированной КП и КПБРМ.
Материалы и методы исследования
В качестве объекта расчетов была выбрана БГМ, близкая по параметрам гусеничному тягачу ГТ-Т. Масса машины с грузом составляет 10400 кг, максимальная скорость движения 45 км/ч (12,5 м/с), габариты (мм): колея 2600, высота 2300, дорожный просвет 450, коэффициент обтекаемости 0,06, КПД трансмиссии 0,9, КПД гусениц при максимальной скорости 0,725, общий КПД машины при максимальной скорости 0,653. Требуемая свободная мощность двигателя 148 кВт, требуемая эффективная мощность 173,2 кВт.
Тяговый расчет машины с указанными параметрами показал, что для неё подходит дизельный двигатель КАМАЗ 740.30-260, параметры внешней скоростной характеристики которого приведены в таблице 1
Таблица 1
Внешняя скоростная характеристика двигателя 740.30-260
| Номинальные обороты двигателя nДN мин-1 | ||||||||
| Номинальный момент двигателя Mд N, Нм | ||||||||
| Номинальная мощность двигателя Nд N, кВт | 103,78 | 133,08 | 158,19 | 175,93 | 188,68 | 193,10 | 192,14 | 0,00 |
| Свободная мощность Nсв N, кВт | 88,70 | 113,74 | 135,20 | 150,37 | 161,27 | 165,05 | 164,22 | 0,00 |
| Свободный момент Mсв N, Нм |
В результате тягового расчета была выбрана пятискоростная КП с передаточными числами: u1= 4,98; u2=3,15; u3= 1,99; u4= 1,26; u5= 0,79.
На первом этапе расчетов для определения времени и пути разгона машины с механической ступенчатой КП использовалась традиционная методика приближенных расчетов, базирующаяся на методе проф. Н.А. Яковлева. В соответствии с этим методом скоростной диапазон разбивается на интервалы, размеры которых при малых скоростях не превышают 3-5 км/ч, на высших передачах 5-7 км/ч. Для каждого из диапазонов определяется время и путь разгона, которые затем суммируются. При этом учитывается время и путь разгона с момента начала движения машины до достижения ею минимальной скорости на первой передаче, а также потери скорости машиной при переключении передач. Методика расчета тягового расчета БГМ изложена в методических указаниях [4].
На втором этапе расчетов определялось время и путь разгона машины, оснащенной КПБРМ. Для этого была разработана специальная программа в форме макроса для книги Excel на языке программирования VBA, которая не приводится из-за ограниченного формата статьи.
Для решения задачи о разгоне БГМ были сначала получены выражения, связывающие скорость и ускорение для каждого этапа разгона, а затем разработана программа, основанная на интегрировании полученных выражений по времени методом Рунге-Кутты 4-го порядка, в результате чего была получена зависимость v=f(t). Ниже приводятся математические уравнения, применяемые при моделировании.
Можно выделить три типовых режима разгона:
– Трогание с места;
– Разгон на фиксированной передаче;
– Переключение передач.
При трогании с места момент на сцеплении нарастает линейно, поэтому система уравнений для определения углового ускорения колёс БГМ имеет вид:
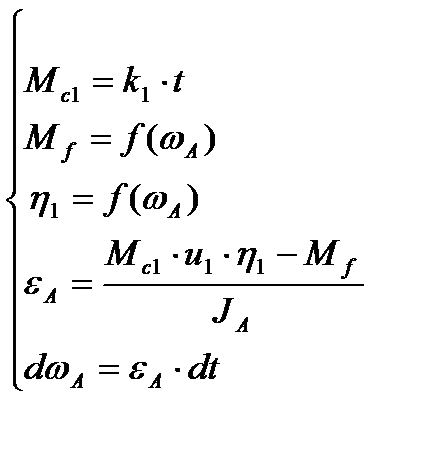 (1)
(1)
где Мс1 – крутящий момент, передаваемый первым сцеплением, Нм;
Мf – крутящий момент от сил сопротивления движению, приведённый к колёсам, Нм;
t – время, с;
JA – момент инерции вращающихся элементов трансмиссии и поступательно движущихся масс БГМ, приведённый к колёсам, кгм2;
ωА – угловая скорость колёс машины, рад/с1;
εА – угловое ускорение колёс машины, рад/с2;
ηi –общий КПД трансмиссии и движителя на i-ой (1-ой) передаче;
ui – передаточное число от сцепления к колёсам на i-ой (1-ой) передаче;
k1 – коэффициент скорости нарастания момента на сцеплении при трогании, Нм/с;
t – время, с;
i – номер включенной передачи
Если момент трения на сцеплении достигает своего предельного значения, то система уравнений несколько меняется:
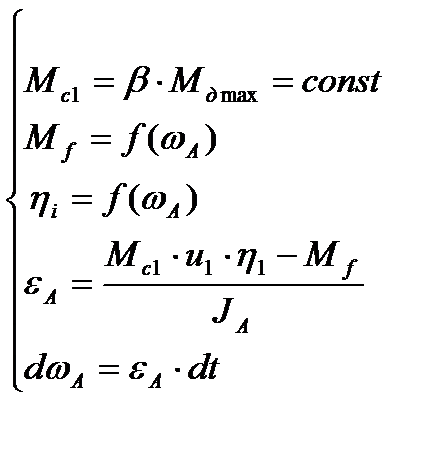 (2)
(2)
где МД max – максимальный крутящий момент двигателя, Нм;
β – коэффициент запаса сцепления;
Будем считать, что двигатель во время трогания управляется таким образом, что к моменту завершения буксования сцепления он имеет частоту вращения 1000 об/мин, начиная с которой работа двигателя сохраняется устойчивой и известна его ВСХ. После того, как скорость БГМ достигнет величины, соответствующей этой частоте вращения двигателя на первой передаче, начинается второй этап разгона, когда между двигателем и колесами есть жёсткая кинематическая связь. Для этого этапа использовался следующая система уравнений:
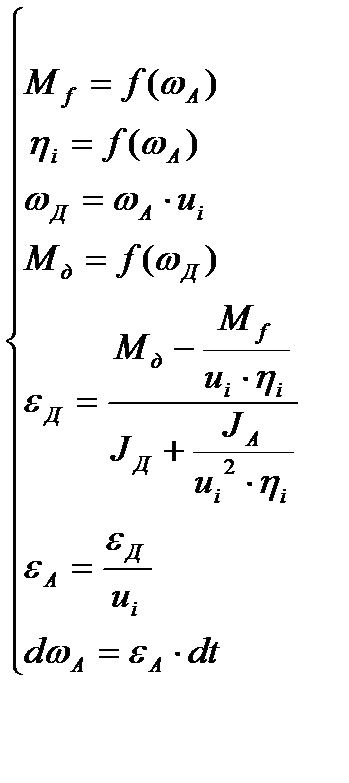 (3)
(3)
где Mд – крутящий момент, развиваемый двигателем, Нм;
JД – момент инерции подвижных элементов двигателя и ведущих частей сцепления, приведённый к маховику, кгм2;
ωД – угловая скорость коленчатого вала ДВС, рад/с1;
εД – угловое ускорение коленчатого вала ДВС;
Отдельный вопрос – переключение передач. Здесь сложность связана с наличием в КП двух сцеплений, работающих с перекрытием. Рассмотрим его подробнее, для чего обратимся к расчётной схеме (рис. 1). При этом для простоты изложения будем считать, что переключение происходит с первой передачи на вторую.
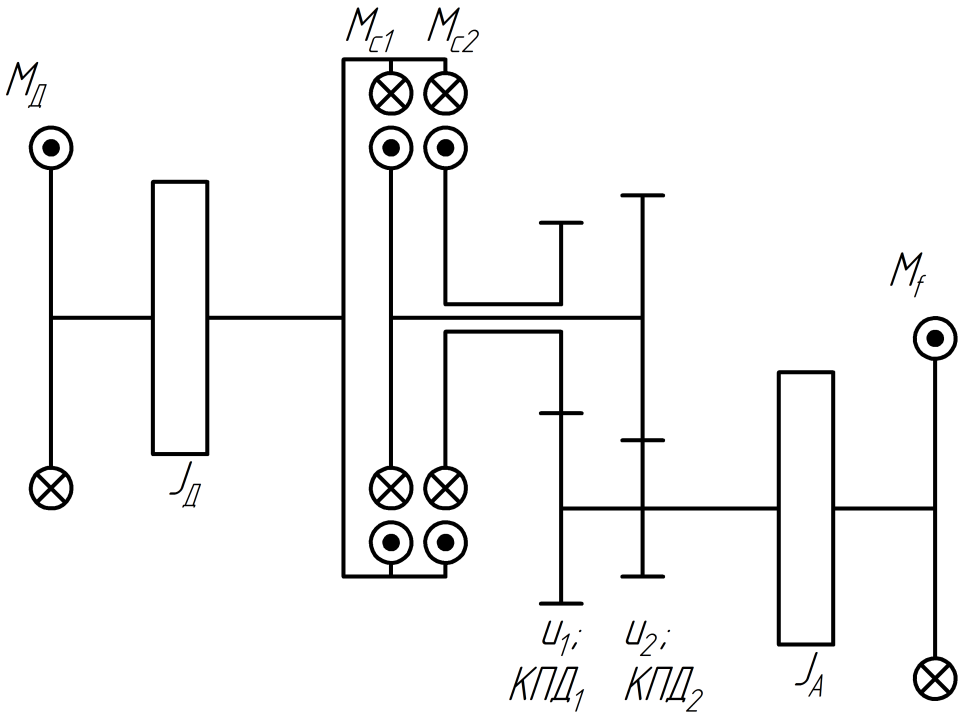
Рис. 1 – Расчётная схема переключения передач
Уравнение равновесия для масс, связанных с ведомым валом JA:
 , (4)
, (4)
где Мс2 – крутящий момент, передаваемый вторым сцеплением, Нм;
Отсюда
 (5)
(5)
На первом этапе переключения, когда нет буксования первого сцепления, угловое ускорение коленчатого вала двигателя может быть выражено через угловое ускорение колёс и передаточное число первой передачи:
 , (6)
, (6)
где ωс1, – угловая скорость ведомого диска первого сцепления, рад/с1
Уравнение равновесия для масс, связанных с двигателем:
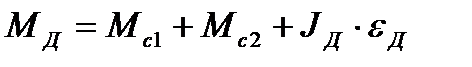 (7)
(7)
Используя полученные ранее выражения для εд (6) и εА (5), получим следующее уравнение:
 (8)
(8)
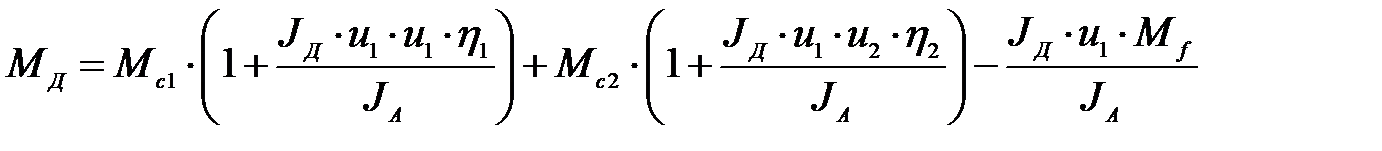 (9)
(9)
Отсюда для момента на первом сцеплении получим:
 (10)
(10)
Зная момент двигателя и момент сопротивления от внешних сил, мы можем определить зависимость между моментами на сцеплениях Mс1 и Мс2.
Пусть в первом приближении момент двигателя, КПД машины и момент сопротивления постоянны, а момент трения на втором сцеплении нарастает линейно. Тогда момент на первом сцеплении будет линейно уменьшаться (рис. 2). При этом целесообразно уменьшать давление в бустере управления первым сцеплением таким образом, чтобы в тот момент, когда крутящий момент, передаваемый первым сцеплением, упадёт до нуля, давление на диски сцепления также исчезло, и сцепление полностью выключилось. В противном случае момент на первом сцеплении станет отрицательным, и в системе возникнет циркуляция мощности. Следует отметить, что на протяжении всего первого этапа переключения в первом сцеплении нет буксования, если передаваемый им момент не превышает максимально возможный, определяемый давлением масла в бустере. Это условие будет выполняться, если давление будет также уменьшаться по линейному закону (основная пунктирная линия на рис. 2).
Первый этап переключения завершается тогда, когда первое сцепление перестаёт передавать крутящий момент. После этого Мс1 в уравнениях можно считать равным нулю. Теперь скорость вала двигателя начинает уменьшаться, выравниваясь со скоростью ведомых дисков второго сцепления, а давление в бустере второго сцепления продолжает нарастать. В зависимости от скорости переключения и коэффициента запаса сцепления возможны два варианта:
1.Давление в бустере второго сцепления достигает максимального значения раньше, чем угловые скорости дисков сцепления выровняются. В этом случае график изменения крутящего момента на втором сцеплении будет иметь так называемую «полку» (этап III на рисунке 2).
2.Угловые скорости выравниваются раньше, чем давление в бустере второго сцепления достигнет максимального значения. В этом случае переключение будет происходить в 2 этапа (этот вариант на рисунке не показан).
В тот момент, когда скорости ведущих и ведомых дисков выравниваются, крутящий момент, передаваемый вторым сцеплением, скачкообразно уменьшается до некоторого значения, соответствующего работе сцепления в обычных условиях без буксования. Это соответствует завершению процесса переключения и переходу трансмиссию в режим разгона на следующей передаче.
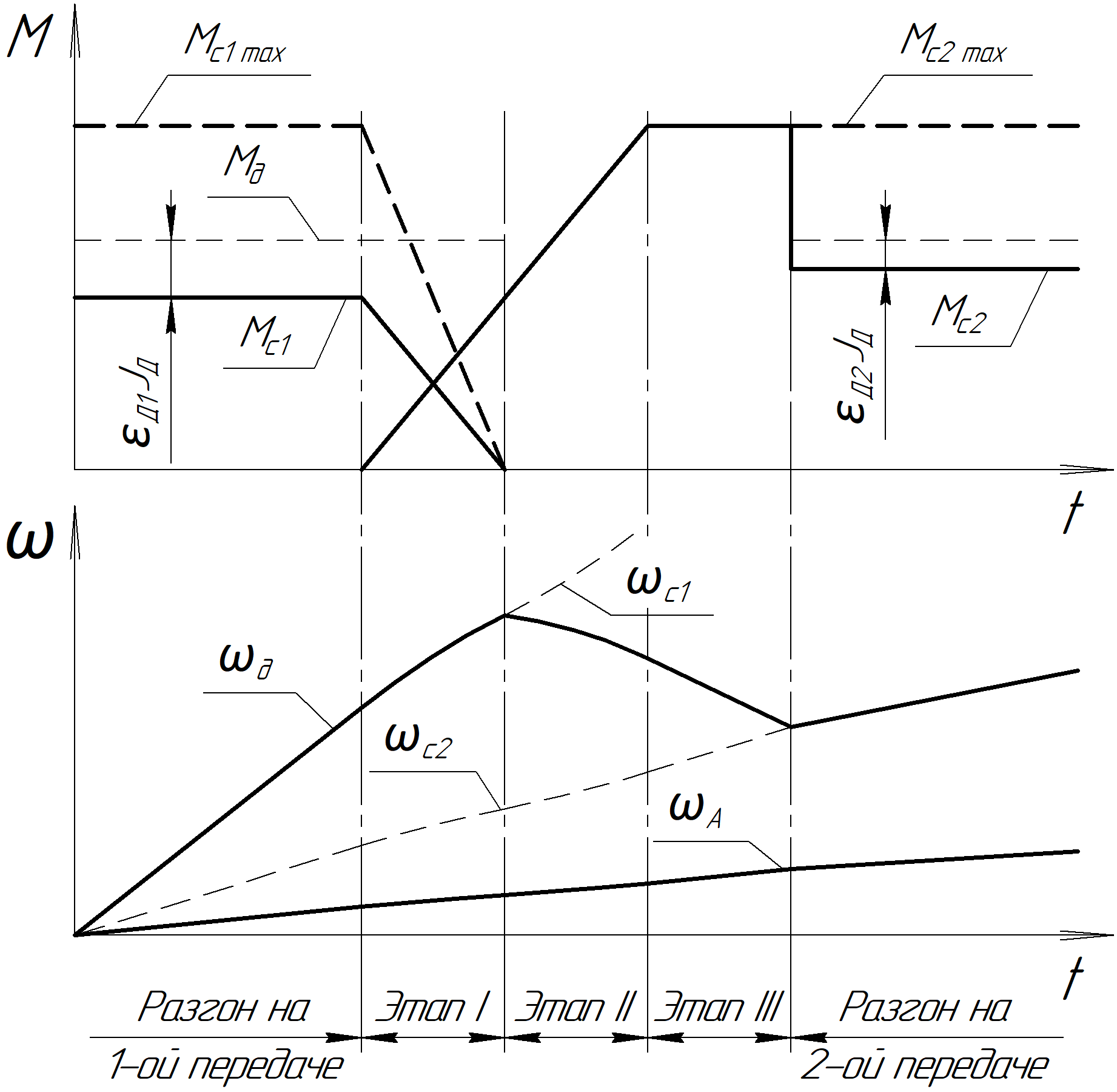
Рис. 2 – Изменение крутящих моментов и угловых скоростей двигателя и сцеплений в процессе переключения
Если же принять во внимание то, что момент двигателя, КПД и момент сопротивления движению являются величинами переменными, то решать задачу о переключении следует пошагово. Система уравнений будет следующая:
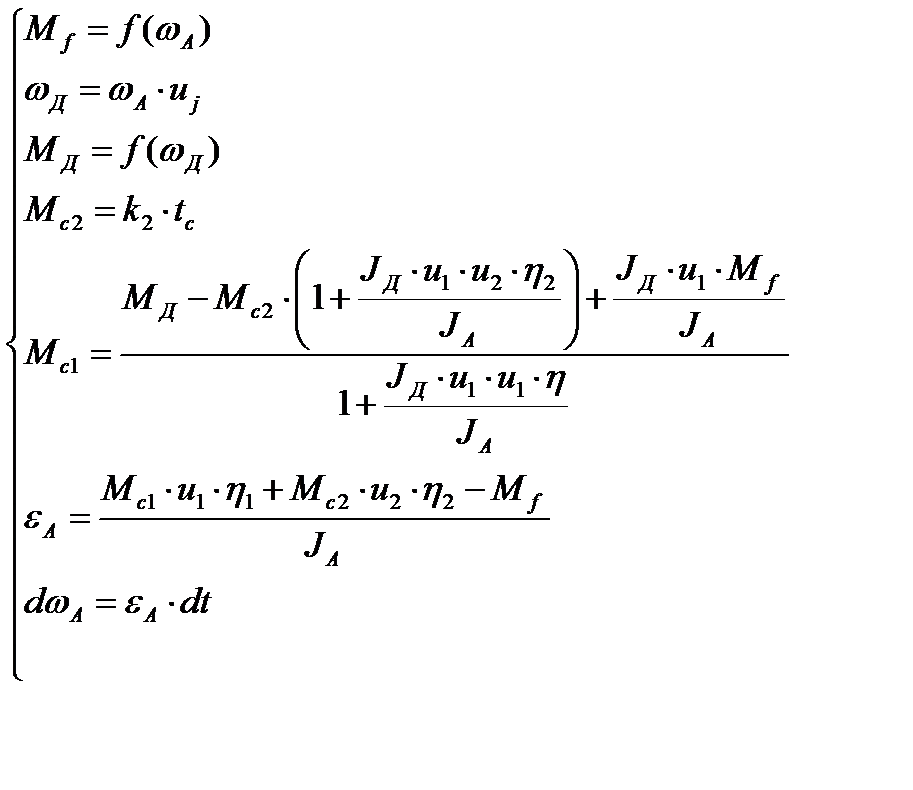 (12)
(12)
где k2 – коэффициент скорости нарастания момента на сцеплении при переключении передач, Нм/с;
tс – время с момента начала включения сцепления, с;
Дополнительные исходные данные для расчета представлены в таблице 2. Они подбирались таким образом, чтобы обеспечить соответствие исходным данным, использованным в произведённом ранее тяговом расчёте. Отдельно следует описать метод определения расчётных моментов инерции движителя Jк и двигателя Jд. В методике [4] используется коэффициент условного приращения массы машины δ, определяемый по формуле
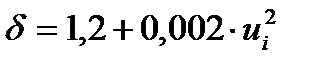
Раскладывая его на составляющие, которыми, в основном, являются поступательно движущаяся масса машины mA, момент инерции движителя Jк и момент инерции двигателя Jд, мы можем получить следующее равенство:
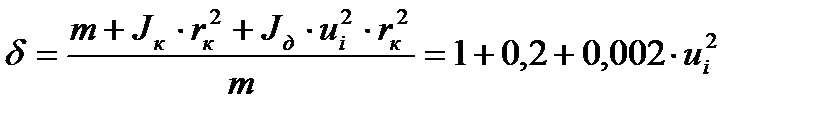 ,
,
из которого можно получить эквивалентные значения Jк и Jд, дающие в результате тот же коэффициент условного приращения массы машины:

Данные для расчета параметров разгона приведены в табл. 2.
Таблица 2
Исходные данные для расчета параметров разгона БГМ с КПБРМ
| Параметры | Обозначение | Переменная | Значение |
| Суммарный момент инерции деталей движителя, кгм2 | Jк | Jk | 157,5 |
| Радиус колеса, м | rк | rk | 0,275 |
| Постоянная составляющая в обеих трансмиссиях | u0 | u0 | 6,40 |
| КПД трансмиссии (не считая КП) | η0 | kpd0 | 0,900 |
| Тип и модель двигателя | Дизель КАМАЗ 740.30-260 | ||
| Минимальные обороты двигателя, мин-1 | nд min | nd_min | |
| Максимальные обороты двигателя,мин-1 | nд max | nd_max | |
| Момент инерции двигателя, кгм2 | Jд | Jd | 1,57 |
| Коэффициент запаса сцепления | β | beta | 1,26 |
| Время включения сцепления при трогании, c | tвкл тр | t_ с vkl_tr | 1,00 |
| Минимальное время включения сцепления, c | tвкл min | t_vkl_min | 0,20 |