Для корректного сравнения результатов расчёта пути и времени разгона машины с различными КП необходимо максимально точно определить время, требуемое на переключение передач. В упоминавшейся ранее методике [4] предлагается для коробок передач с синхронизаторами принимать время переключения передач равным 2 с. Полученное при этом допущении общее расчётное время разгона до скорости 40 км/ч составляет 20,04 с. При этом расчётный путь, проходимый машиной до достижения максимальной скорости, составляет 117,3 м.
Для современных коробок передач время переключения может исчисляться долями секунды, поэтому нами был рассмотрен известный прототип КП. Ориентируясь на момент инерции сцепления и размеры синхронизаторов, мы оценили время синхронизации при переключениях по методике, изложенной в учебнике [5]. Принятые для расчётов данные представлены в табл. 3
Таблица 3
Данные для расчёта времени синхронизации
| i | I | II | III | IV | V |
| u | 4,98 | 3,15 | 1,99 | 1,26 | 0,79 |
| Mсинхр | 112,7 | 92,8 | 46,2 | 35,5 | |
| Jсинхр прив | 7,440 | 2,977 | 1,188 | 0,476 | 0,187 |
Эти же данные мы использовали для расчёта разгона машины с КПБРМ, где они понадобились для определения времени, затрачиваемого на предвключение передачи. Здесь подразумевается, что коробка передач построена по схеме с двойным сцеплением (рис. 3), при которой все нечётные передачи включаются с одного сцепления, а чётные – с другого. В этом случае для осуществления переключения необходимо, чтобы за время разгона на одной из передач сцепление следующей передачи успело синхронизироваться с выходным валом КП, т.е. чтобы произошло предвключение. Поскольку время разгона на низших передачах мало, оно может оказаться меньше времени предвключения следующей передачи, и в этом случае переключение произойдёт с задержкой.

Рис. 3 – Схема четырёхступенчатой КПБРМ с двойным сцеплением (из патента SU 846328 завода имени Лихачёва, 1979 г.)
Для того, чтобы исключить погрешность, вносимую методикой расчёта, моделирование разгона машины с обеими КП мы производили в одной и той же программе.
Результаты исследования представлены на рис. 4 и 5 в виде графиков зависимости времени и пути разгона от скорости БГМ, оборудованной механической ступенчатой КП и механической КПБРМ.
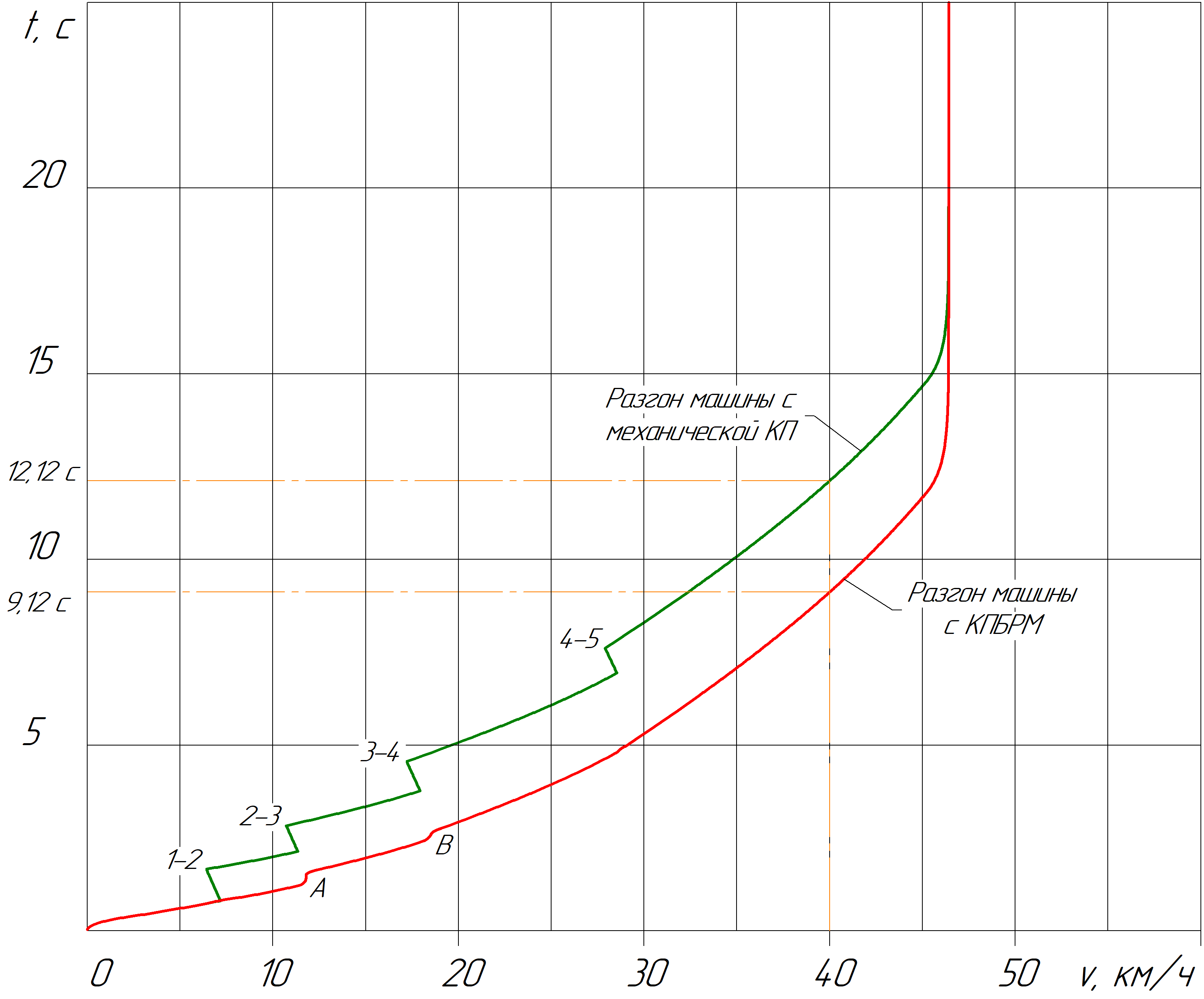
Рис. 4 – Сравнение характеристик разгона машин с механической ступенчатой КП и с КПБРМ по времени
На графике рис. 4 показана зависимость времени разгона от скорости для БГМ, оборудованной механической ступенчатой КП при условии, что время переключения вычисляется с учётом реального времени синхронизации. Как можно увидеть, скорость 40 км/ч достигается через 12,12 с. На этом же рис. показана характеристика разгона для машины с КПБРМ, из которой видно, что переключения передач происходят плавно, без снижения скорости. Как следствие, время разгона БГМ до 40 км/ч уменьшается на 3 с или примерно в 1,3 раза и составляет 9,12 с. При этом можно заметить небольшие задержки переключений на третью и четвертую передачи (участки А и В на графике) из-за малого времени разгона на этих передачах сравнительно c временем предвключения, о чем говорилось ранее.
На рис. 5 приведены характеристика разгона БГМ по пути. Суммарный путь, проходимый БГМ за время разгона до 40 км/ч, оснащённой механической синхронизированной КП, составил 76,7 м, в то время как этот же показатель для машины с КПБРМ равен 63,3 м, что в 1,2 раза меньше.

Рис. 5 – Сравнение характеристик разгона машин с механической тупенчатой КП и с КПБРМ по пути
Сравнение этих результатов с теми, что были получены приближенным методом графо-аналитического интегрирования проф. Н.А.Яковлева [4], показывает существенную разницу, которая, прежде всего, объясняется завышенными значениями времени переключения передач. Так полученное время разгона отличается на 65%, а путь – на 53%. Однако даже если использовать в расчётах время переключения передач, равное реальному времени синхронизации, разница составит порядка 15-20%.
Главная причина этого – различный способ учёта инерции вращающихся масс. В классической методике для расчёта ускорения машины используются формулы

При этом получается, что на разгон двигателя, момент инерции которого учтён коэффициентом условного приращения массы машины δ, затрачивается часть крутящего момента двигателя, уже умноженного на КПД трансмиссии. В методике же, положенной в основу использованной нами программы, ускорение определяется иначе. Например, для моделирования разгона в пределах одной передачи:

Здесь на КПД умножаться только та часть крутящего момента двигателя, которая затрачивается на разгон колёс и поступательно движущихся масс. В результате ускорения, полученные по методике проф. Яковлева, оказываются несколько меньше. Частично устранить эту разницу можно, закладывая КПД в коэффициент условного приращения массы машины:

Однако при этом должно учитываться, что КПД гусеничной машины зависит от скорости движения. Но это не обеспечивается при использовании в классическом расчёте формулы вида
 ,
,
где А и В – некоторые постоянные числовые коэффициенты. Из этого следует, что предлагаемая нами методика является более точной.
Полученные результаты исследований говорят о положительном влиянии установки КПБРМ вместо механической ступенчатой КП на параметры разгона БГМ, а также об эффективности разработанного метода определения параметров разгона БГМ и специальной программы расчета.
Выводы
1.Разработаны программа и алгоритм решения дифференциального уравнения  при начальных условиях t=0, v=0 в форме макроса для книги Excel на языке программирования VBA. В отличие от широко применяющегося графоаналитического метода определения тягово-скоростных характеристик транспортных колесных и гусеничных машин, программа автоматизирует расчеты и позволяет получить более точные результаты.
при начальных условиях t=0, v=0 в форме макроса для книги Excel на языке программирования VBA. В отличие от широко применяющегося графоаналитического метода определения тягово-скоростных характеристик транспортных колесных и гусеничных машин, программа автоматизирует расчеты и позволяет получить более точные результаты.
2. С помощью разработанной программы были выполнены расчеты параметров разгона (пути и времени разгона) БГМ, оборудованной двумя различными КП: механической ступенчатой и коробкой передач без разрыва потока мощности. Разгон во втором случае происходил более плавно, а время и путь разгона оказались ниже соответственно в 1,3 и в 1,2 раза за счет снижения потерь скорости в процессе переключения передач.
3. Разработанная программа и алгоритм решения соответствующего дифференциального уравнения могут быть применены при решении аналогичных задач для других типов транспортных машин, в том числе автомобилей.
4. Поскольку БГМ являются машинами двойного применения, улучшенные параметры разгона могут иметь большое значение для улучшения такой важной тактико-технической характеристики, как подвижность.
Литература
1. Забавников Н.А. Основы теории транспортных гусеничных машин. М.: Машиностроение,1975. - 448 с.
2. Гусеничные транспортеры-тягачи / Под ред. В.Ф. Платонова. М.: Машиностроение, 1978. – 351 с.
3. Многоцелевые гусеничные шасси. В.Ф. Платонов, В.А. Коробкин, С.В. Платонов; под редакцией В.Ф. Платонова – М.: Машиностроение, 1998 – 342 с.
4. Парфенов А.П., Щетинин Ю.С. Тяговый расчет гусеничной транспортно-тяговой машины. Методические указания для выполнения курсовой работы «Теория колесных и гусеничных транспортно-тяговых машин» для студентов специальности 150100 «Автомобиле- и тракторостроение». – М.: МГТУ «МАМИ», 2002. – 75 с
5. Шарипов В.М. Конструирование и расчёт тракторов: Учебник для студентов вузов. 2-е изд. перераб. и доп. – М.: Машиностроение, 2009. – 752с.