Логические операции над высказываниями

Тема 2. Высказывания. Логические операции над ними

Простое высказывание – это утверждение (повествовательное предложение), в отношении которого можно сказать, истинно оно или ложно (но не то и другое вместе).

Всякое высказывание является предложением и может быть выражено словами, однако далеко не каждое предложение является высказыванием в математическом смысле.

Пример. Не являются высказываниями предложения:

1) число 0,00000001 очень мало;

2) существует ли число, квадрат которого равен 2?

3) ;

4) .

Первое их этих предложений не является высказыванием потому, что не имеет точного смысла и мы не можем сказать, истинно оно или ложно; второе предложение содержит вопрос; третье и четвертое предложения содержат букву х. При одних значениях х получается истинное высказывание, при других ложное.

Предложение, о котором невозможно однозначно решить вопрос, истинно оно или ложно, высказыванием не является.

Всякое высказывание является либо истинным, либо ложным (закон исключенного третьего).

Никакое высказывание не может быть одновременно истинным и ложным (закон противоречия).

Неопределенные высказывания

Будем обозначать через N множество всех натуральных чисел. Через х обозначим произвольный элемент множества N. Рассмотрим следующие предложения:

,

,

,

.

Предложения A(x), B(x), C(x), D(x) высказываниями не являются, т.к. об истинности, например, A(x) мы ничего не можем сказать, пока нам не известно число х. Однако, подставляя в A(x) вместо х различные натуральные числа, мы будем получать высказывания о натуральных числах – иногда истинные, иногда ложные. Например:

- истинное высказывание;

- ложное высказывание.

Предложения A(x), B(x), C(x), D(x), содержащие переменную х, называют неопределенными высказываниями (предикатами). Если вместо х подставить число, то мы получим обычное высказывание.

Неопределенное высказывание может быть задано на любом множестве. Оно представляет собой высказывание о каком-то элементе х рассматриваемого множества.

Часто приходится рассматривать неопределенные высказывания, в которые входит не одно, а два или большее число переменных.

Пример. ;

;

;

.

Мы ничего не можем сказать об истинности или ложности этих утверждений, т.к. нам неизвестны х и y. Но если точно указано, чему равны х и y, каждое из сформулированных утверждений превращается в высказывание – для одних пар х и y истинное, для других – ложное. Вот примеры высказываний, полученных из указанных предложений при конкретных значениях х и y:

- истинное высказывание;

- ложное высказывание;

- ложное высказывание;

- ложное высказывание;

- истинное высказывание.

Логические операции над высказываниями

Высказывания обозначают латинскими буквами A, B, C, …, их значения истина и ложь соответственно, через «И» и «Л». Сложные высказывания получают из простых при помощи логических операций, к которым относятся отрицание, конъюнкция, дизъюнкция, импликация, эквивалентность (эквиваленция).

1. Если А – высказывание, то отрицание высказывания А определяется как такое высказывание, которое истинно тогда и только тогда, когда высказывание А ложно. Отрицание высказывания А обозначается (или Ø А) и читается «не А».

Истинность-ложность операции отрицания выражает истинностная таблица 1.1.

Т а б л и ц а 1.1

 

А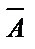
И	Л
Л	И

Пример. 1) ; .

2) ; .

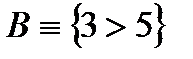3) ; .

4) ; .

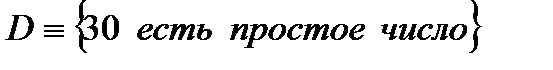Каково бы ни было высказывание А, из двух высказываний А, А одно является истинным, а другое – ложным.

Закон отрицания отрицания: Двойное отрицание А истинно в том и только в том случае, если истинно само высказывание А (т.е. если А истинно, то и А истинно, а если А ложно, то и А ложно).

2. Конъюнкцией двух высказываний называется такое высказывание, которое истинно тогда и только тогда, когда оба составляющие ее высказывания истинны.

Если А, В - высказывания, то их конъюнкция обозначается A Ù B (или А & B) и читается «А и В ».

Конъюнкции соответствует истинностная таблица 1.2.

Т а б л и ц а 1.2

 

А	В	А Ù В
И	И	И
И	Л	Л
Л	И	Л
Л	Л	Л

Пример: Высказывание - истинно, высказывание - истинно, поэтому истинна и их конъюнкция .

3. Дизъюнкцией двух высказываний называется такое высказывание, которое ложно тогда и только тогда, когда оба составляющие ее высказывания ложны.

Если А, В - два высказывания, то их дизъюнкция обозначается А Ú В и читается «А или В ». Союз «или» здесь употребляется в соединительном, а не в разделительном смысле, т. е. для истинности высказывания А Ú В допускается также случай истинности обоих высказываний А, В.

Операции дизъюнкции соответствует истинностная таблица 1.3.

Т а б л и ц а 1.3

 

А	В	А Ú В
И	И	И
Л	И	И
И	Л	И
Л	Л	Л

Пример: Высказывание - истинно, высказывание - ложно. Тогда высказывание - истинно.

4. Импликация высказываний А, В определяется как такое высказывание, которое ложно тогда и только тогда, когда высказывание А истинно, а высказывание В ложно. Импликация двух высказываний А, В обозначается А Þ В и читается «если А, то В ». Высказывание А называется посылкой импликации, а В - заключением.

Импликации соответствует истинностная таблица 1.4.

Т а б л и ц а 1.4

 

А	В	А Þ В
И	И	И
Л	И	И
И	Л	Л
Л	Л	И

 

5. Эквивалентность двух высказываний А, В определяется как высказывание, которое истинно тогда и только тогда, когда высказывания А, В оба истинны или оба ложны. Обозначается А Û В и читается «А тогда и только тогда, когда В » («если А, то В, и, если В, то А », «А есть необходимое и достаточное условие для В »). Значения эквивалентности определены в истинностной таблице 1.5.

Т а б л и ц а 1.5

А	В	А Û В
И	И	И
И	Л	Л
Л	И	Л
Л	Л	И

 

Пример: Рассмотрим два высказывания, определенных на множестве натуральных чисел:

;

.

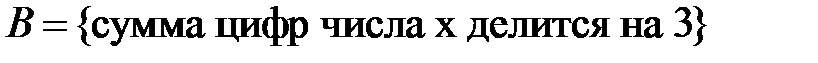Тогда признак делимости на 3 можно записать как (число делится на 3 тогда и только тогда, когда сумма его цифр делится на три).

Если теорема сформулирована в виде A Þ B, то она называется признаком или достаточным условием для B, где A, B – некоторые высказывания.

Теорема типа В Þ А называется обратной для теоремы A Þ B.

Если теорема имеет вид A Û B, то она называется критерием или необходимым и достаточным условиями для B.

Теорема такого типа объединяет прямую и обратную теоремы.

Теорема типа называется противоположной к обратной теореме.

Высказывание A Þ B истинно тогда и только тогда, когда истинно высказывание . На этом факте основан метод доказательства от противного.

Пример: Пусть высказывание , а . Тогда .

Данную теорему принято выражать в следующем виде:

А является достаточным условием для В.

В является необходимым условием для А.

Необходимое условие можно сформулировать следующим образом: для делимости числа х на 4 необходимо, чтобы его последняя цифра была четной.