Граф – множество точек (вершин графа), часть из которых соединена линиями (ребрами графа).
Ребро, соединяющее вершину с ней же, называется петлей.
Если вершины соединяются направленными линиями (дугами графа), то граф называют ориентированным (орграфом).
Вершины графа, связанные ребром, называются смежными. В таком случае говорят, что их общее ребро инцидентно обеим вершинам.
Если граф ориентированный, то одна из вершин дуги является начальной, а вторая – конечной.
Степенью вершины называется количество ребер, ей инцидентных. В орграфе число дуг, входящих в вершину и выходящих из нее, называется соответственно полустепенью входа и полустепенью выхода вершины.
Простейшие свойства степеней вершин графа:
1. Сумма степеней вершин графа равна удвоенному числу его ребер.
2. Число вершин нечетной степени четно.
Вершина, не инцидентная никакому ребру, называется изолированной.
Граф, состоящий только из изолированных вершин, называется пустым или нуль-графом.
Граф называется полным, если любые две его вершины являются смежными.
Подграф заданного графа – это граф, множества вершин и ребер которого являются подмножествами соответственно множеств вершин и ребер исходного графа.
Маршрут (путь) – чередующаяся последовательность вершин и ребер, в которой каждые два соседних элемента инцидентны.
Количество ребер при этом называется длиной маршрута.
Цепь – маршрут, в котором все ребра различны.
Простая цепь – цепь, в которой все вершины различны.
Цикл (простой цикл) – замкнутая (простая) цепь.
Граф называется связным, если для любых двух его вершин найдется соединяющий их маршрут. Если хотя бы для одной пары вершин это свойство не выполняется, то граф называется несвязным.
Цикл, проходящий через все ребра графа ровно один раз, называется эйлеровым, а граф, его содержащий, - эйлеровым графом. Связный граф является эйлеровым тогда и только тогда, когда все его вершины четной степени.
Цикл, проходящий через все вершины графа ровно один раз, называется гамильтоновым, а граф, его содержащий, - гамильтоновым графом.
Дерево – связный граф без циклов.
Корневое дерево – дерево, в котором выделена одна из вершин (корень).
Способы задания графа:
1. Графический: вершины графа изображаются точками, а ребра и дуги – линиями, их соединяющими (в дугах указывается направление с помощью стрелки).
2. Аналитический: представляется описание множеств 
и 
, так как граф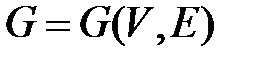 
может быть определен как совокупность двух множеств: 
, элементы которого называются вершинами, и 
- произвольное множество пар 
, элементы которого называются дугами.
3. Матричный: используются матрицы графов.
Матрица смежности неориентированного графа 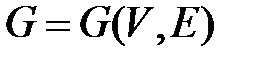- квадратная матрица 
порядка 
, где 
- количество вершин. Ее элементы 
равны числу ребер, соединяющих вершины 
и 
.
Пример 1. В поселке 6 стационарных телефонов. Можно ли каждый из них соединить кабелем ровно с тремя другими? Изменится ли ответ, если добавить еще один телефон?
Решение: Построим граф, вершины которого будут соответствовать телефонам, а ребра – проводам, их соединяющим. По условию задачи каждый телефон должен быть соединен ровно с тремя другими. Соединим каждую вершину графа ровно с тремя другими, например, так, как показано на рис. 1.
Если телефонов станет 7, то, согласно второму свойству степеней вершин графа, требуемую схему реализовать невозможно. Действительно, степень каждой вершины по условию должна быть равна трем (каждый телефон соединен ровно с тремя другими, т.е. каждая вершина графа инцидентна трем ребрам). Получается, что в графе количество вершин нечетной степени нечетно, а этого не может быть. Значит, при добавлении одного аппарата соединение не может быть реализовано.
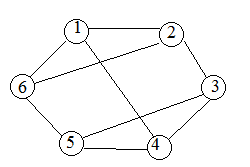Рис. 1
Пример 2. Между городами A, B, C, D, E, F, G, H организовано автобусное сообщение по следующей схеме: A-B, A-C, A-D, B-C, D-C, C-E, F-G, F-H, G-H. Определить, можно ли доехать на рейсовом автобусе из города А в город Е и G. Если да, то определить маршрут с наименьшим числом пересадок.
Решение: Построим граф с вершинами, соответствующими городам. Соединим ребром те вершины, которые соответствуют городам с автобусным сообщением. В результате получен граф, состоящий из двух связных подграфов, между которыми нет ни одного маршрута.
Из рисунка видно, что проехать из города А в город Е можно тремя маршрутами: A-B-C-E, A-C-E, A-D-C-E. Самый короткий путь – через С (одна пересадка).В город G рейсовым маршрутом из А попасть нельзя, так как построенный граф не является связным, а города А и G соответствуют вершинам подграфов, любые две вершины которых (взятые по одной из каждого графа) не являются смежными.
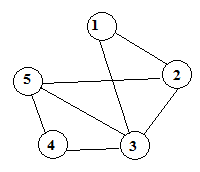
Пример 3. Построить граф, для которого задана матрица смежности:
Решение: Изобразим 5 вершин графа точками на плоскости и соединим вершину 
с вершиной 
линией, если элемент 
.
КОНТРОЛЬНЫЕ ВОПРОСЫ:
1. Что такое граф?
2. Как определяется степень вершины?
3. Назовите свойства степеней вершин.
4. Дайте определение маршруту.
5. Что такой цикл?
6. Какой граф называется эйлеровым?
7. Дайте определение дереву.
8. Какими способами можно задать граф?
Домашнее задание: [3], §7.1, 7.2