Топливные отсеки, конструктивно представляющие собой тонкостенные оболочки с силовым набором, являются составной частью корпуса большинства ракет. Оболочки баков и частично заполняющее их жидкое топливо образуют единую систему, в которой могут происходить совместные колебания.
Динамические характеристики баков с жидким топливом в значительной степени влияют на продольную устойчивость ракет.
Определяя формы и частоты продольных колебаний жидкости в упругой оболочке, возмущение давления в районе заборного устройства топливной емкости и другие характеристики, будем считать жидкость идеальной и несжимаемой, а ее движение безвихревым. Предположим, что ракета и ее топливные баки осесимметричны с одинаковыми распределениями масс и жесткостей в любом радиальном направлении. Будем рассматривать прямолинейный полет с постоянным продольным ускорением, при котором невозмущенные свободные поверхности топлива в баках перпендикулярны продольной оси ракеты.
В возмущенном движении, вызванном каким-либо осесимметричным по отношению к ракете фактором, будем учитывать только осесимметричные колебания жидкости и упругой оболочки. При этом движение в жидкости будет также обладать свойством осевой симметрии. Деформацию свободной поверхности жидкости в баках при колебаниях учитывать не будем. Предположим, что колебания топлива вызваны изменением радиуса бака из-за изменения давления, а не вследствие деформации растяжения или сжатия оболочки. Стенки баков будем считать тонкостенными безмоментными оболочками. Колебания корпуса и баков с жидким топливом будем предполагать малыми, что позволит применять линеаризованные уравнения деформации оболочки и движения жидкости.
При оговоренных допущениях можно записать дифференциальные уравнения колебаний оболочки
 (1)
(1)
где  дифференциальные операторы;
дифференциальные операторы;  проекции вектора перемещения оболочки на оси координат
проекции вектора перемещения оболочки на оси координат 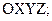
 и
и  плотность материала оболочки и ее толщина;
плотность материала оболочки и ее толщина;  проекции вектора внешних распределенных сил, действующих на оболочку, на оси
проекции вектора внешних распределенных сил, действующих на оболочку, на оси  .
.
В число внешних по отношению к оболочке бака сил необходимо включить не только продольные силы, действующие со стороны смежных отсеков, но и давление жидкости на смачиваемую поверхность бака  и давление газов наддува на несмоченную поверхность бака
и давление газов наддува на несмоченную поверхность бака 
Движение жидкости в баке должно удовлетворять уравнению Лапласа
 (2)
(2)
Уравнения (1) и (2) дополняют граничными и начальными условиями. Для оболочки граничными условиями могут быть соотношения между перемещениями  заданные на некотором контуре
заданные на некотором контуре  в виде
в виде
 на
на  (3)
(3)
Граничными условиями для потенциала скоростей  жидкости являются условия непротекания на смоченной поверхности бака
жидкости являются условия непротекания на смоченной поверхности бака
 на
на  (4)
(4)
где  перемещение оболочки по нормали к поверхности, и линеаризованные динамические условия на смоченной и свободной поверхностях (индекс номера бака
перемещение оболочки по нормали к поверхности, и линеаризованные динамические условия на смоченной и свободной поверхностях (индекс номера бака  для простоты опускаем)
для простоты опускаем)
 на
на  (5)
(5)

 на
на  (6)
(6)
Так как оценивать устойчивость продольного движения ракеты удобно с помощью частотных методов, позволяющих анализировать поведение объекта при разнообразных возмущениях, в дальнейшем будем исследовать собственные продольные колебания и определять динамические характеристики упругой оболочки с жидким топливом без учета движений, которые вызваны начальными условиями.
Решим задачу, описываемую уравнениями (1)…(6), на примере цилиндрического топливного бака. При этом для определения характеристик собственных колебаний емкости с топливом сначала рассмотрим колебания упругой цилиндрической оболочки бака с жестким дном, затем решим задачу о колебаниях жидкости в баке с жесткой обечайкой и упругим плоским дном. Представим потенциал скоростей в виде

где  потенциал скоростей жидкости в баке с упругой цилиндрической оболочкой и жестким дном;
потенциал скоростей жидкости в баке с упругой цилиндрической оболочкой и жестким дном;  потенциал скоростей жидкости в баке с жесткой цилиндрической обечайкой и упругим дном.
потенциал скоростей жидкости в баке с жесткой цилиндрической обечайкой и упругим дном.
Сформулируем и решим обе частные задачи.
Рассмотрим круговой цилиндрический бак радиуса  с упругой обечайкой и жестким дном. Определим потенциал скоростей
с упругой обечайкой и жестким дном. Определим потенциал скоростей  и радиальную деформацию обечайки бака
и радиальную деформацию обечайки бака 
Запишем уравнение Лапласа в цилиндрических координатах для осесимметричных колебаний
 (7)
(7)
и граничные условия на смоченных поверхностях
 при
при 
 (8)
(8)
 при
при 
 (9)
(9)
Предполагая, что деформация свободной поверхности отсутствует, а уровень жидкости в баке и кажущееся ускорение не меняются, динамическое условие (6) с точностью до постоянной величины представим в виде
 при
при  (10)
(10)
Предполагая, что боковые стенки и жидкость совершают гармонические колебания, и используя метод Фурье, будем искать решение уравнения (7) в виде ряда
 (11)
(11)
Функция  характеризующая радиальную деформацию стенок бака, строится так, чтобы удовлетворялось условие (8):
характеризующая радиальную деформацию стенок бака, строится так, чтобы удовлетворялось условие (8):
 (12)
(12)
Подставляя частное решение вида (11) в (7), получим равенство
 (13)
(13)
Левая часть равенства (13) не зависит от переменной  а правая часть – от переменной
а правая часть – от переменной  Поэтому обе части равенства (13) представляют собой некоторую константу. Обозначим ее через
Поэтому обе части равенства (13) представляют собой некоторую константу. Обозначим ее через  и из (13) получим для функции
и из (13) получим для функции  и
и  два линейных дифференциальных уравнения второго порядка
два линейных дифференциальных уравнения второго порядка
 (14)
(14)
 (15)
(15)
Последнее уравнение называют уравнением Бесселя. Так как потенциал скоростей  при
при  является ограниченной функцией, обладающей свойством симметрии, в качестве решения уравнения (15) может рассматриваться функция Бесселя первого рода нулевого порядка
является ограниченной функцией, обладающей свойством симметрии, в качестве решения уравнения (15) может рассматриваться функция Бесселя первого рода нулевого порядка  если
если  мнимое число, или модифицированная функция Бесселя первого рода нулевого порядка
мнимое число, или модифицированная функция Бесселя первого рода нулевого порядка  если
если  вещественное число.
вещественное число.
Чтобы найти решение уравнения (14), необходимо записать граничные условия для функции  Подставив (11) в (9), найдем
Подставив (11) в (9), найдем
 при
при 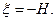 (16)
(16)
Кроме того,
 при
при  (17)
(17)
так как деформация свободной поверхности отсутствует по предположению.
Равенства (16) и (17) одновременно могут выполняться только при условии, что  вещественное число. Поэтому решением уравнения (14) будут функции
вещественное число. Поэтому решением уравнения (14) будут функции
 (18)
(18)
Здесь  поскольку днище бака абсолютно жесткое и при
поскольку днище бака абсолютно жесткое и при  должно выполняться условие
должно выполняться условие

Решениями уравнения (15) при вещественных  являются модифицированные функции Бесселя
являются модифицированные функции Бесселя
 (19)
(19)
где

Подставляя (18), (19) в (11), (12), получим
 (20)
(20)
 (21)
(21)
Определим частоту собственных упругих колебаний бака с жидкостью 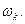 Составим уравнения колебаний цилиндрической оболочки в радиальном направлении. Изменение радиуса оболочки на величину
Составим уравнения колебаний цилиндрической оболочки в радиальном направлении. Изменение радиуса оболочки на величину  вызвано возмущением давления в жидкости
вызвано возмущением давления в жидкости
 при
при 


При упругой деформации цилиндрической стенки, плотность материала которой  а толщина
а толщина  возникает растягивающая сила
возникает растягивающая сила 
Учитывая предположения об идеальности жидкости и отсутствии демпфирования колебаний конструкции при деформации, запишем уравнение колебаний элемента оболочки в радиальном направлении

или
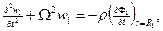 (22)
(22)
где  частота собственных радиальных колебаний контура кольца единичной длины.
частота собственных радиальных колебаний контура кольца единичной длины.
С учетом формул (20), (21) вместо (22) запишем
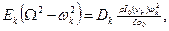 (23)
(23)
а из соотношения (8) получим

или
 (24)
(24)
так как
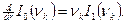
Подставляя (24) в (23), найдем частоту собственных колебаний бака с жидкостью
 (25)
(25)
Сформулируем и решим задачу определения потенциала скоростей жидкости  в цилиндрическом баке с жесткой обечайкой и упругим дном. В большинстве случаев днище баков является пологой оболочкой, образующая которой – окружность или эллипс.
в цилиндрическом баке с жесткой обечайкой и упругим дном. В большинстве случаев днище баков является пологой оболочкой, образующая которой – окружность или эллипс.
Сформулируем краевые задачи для определения функций  и
и  Потенциал скоростей жидкости должен удовлетворять уравнению Лапласа
Потенциал скоростей жидкости должен удовлетворять уравнению Лапласа

 (26)
(26)
и граничным условиям
 при
при  (27)
(27)
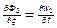 при
при  (28)
(28)
 при
при  (29)
(29)
Прогиб пологой сферической оболочки  в направлении ее радиуса кривизны
в направлении ее радиуса кривизны  может быть найден из решения уравнения собственных осесимметричных колебаний
может быть найден из решения уравнения собственных осесимметричных колебаний

где 

 жесткость единицы длины оболочки на изгиб;
жесткость единицы длины оболочки на изгиб;  модуль Юнга;
модуль Юнга;  коэффициент Пуассона.
коэффициент Пуассона.
Предполагая, что радиус кривизны сферического днища достаточно большой, заменим сферу плоской круглой пластиной, имеющей прогиб  . Пренебрегая величинами порядка
. Пренебрегая величинами порядка  запишем краевую задачу о собственных колебаниях пластины с жестко закрепленными краями:
запишем краевую задачу о собственных колебаниях пластины с жестко закрепленными краями:

 (30)
(30)
 при
при  (31)
(31)
 при
при  (32)
(32)
где

Для решения задачи (30)…(32) применим метод разделения переменных. Будем искать решение в виде

Из уравнения (30) получим
 (33)
(33)
 (34)
(34)
где

Вместо (31), (32) запишем граничные условия

 (35)
(35)
Функции  при
при  должно быть ограниченным. Поэтому решением уравнения (34) будет
должно быть ограниченным. Поэтому решением уравнения (34) будет

Подставляя данное решение в (35), получим

 при
при 

 при
при  (36)
(36)
Константы  и
и  не должны одновременно обращаться в нуль, так как мы ищем нетривиальное решение
не должны одновременно обращаться в нуль, так как мы ищем нетривиальное решение  . Следовательно, определитель системы (36) нужно приравнять нулю и записать трансцендентное уравнение
. Следовательно, определитель системы (36) нужно приравнять нулю и записать трансцендентное уравнение
 (37)
(37)
Его корни  собственные числа краевой задачи о колебаниях пластины
собственные числа краевой задачи о колебаниях пластины  лучим соотношение между коэффициентами
лучим соотношение между коэффициентами  и
и 
 (38)
(38)
Полагая  запишем окончательное выражение для собственных функций
запишем окончательное выражение для собственных функций
 (39)
(39)
Собственные функции ортогональны с весом 
 при
при 
Нормирующий множитель 
Решение уравнения (33) представим в виде
 (40)
(40)
где  собственная частота колебаний.
собственная частота колебаний.
Если заданы начальные значения  ;
;  деформацию днища бака можно описать функцией
деформацию днища бака можно описать функцией
 (41)
(41)
где



Нетрудно показать, что поперечные колебания круглой пластины, вызываемые равномерно распределенным давлением  описываются функцией
описываются функцией

Потенциал скоростей  построим так, чтобы удовлетворялись равенства (26) и (29):
построим так, чтобы удовлетворялись равенства (26) и (29):
 (42)
(42)
Подставив (42) в (27), запишем трансцендентное уравнение
 (43)
(43)
Корни этого уравнения


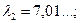
 …
…
являются собственными числами краевой задачи (26)…(28). Чтобы выразить функции времени 
 через
через 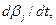 подставим (41) и (42) в условие (28):
подставим (41) и (42) в условие (28):

Умножив обе части данного равенства сначала на 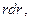 затем на
затем на  и проинтегрировав по
и проинтегрировав по  в пределах от
в пределах от  до
до  получим
получим
 (44)
(44)
Здесь коэффициенты 
 определяются через значения функций Бесселя при
определяются через значения функций Бесселя при 

Таким образом, потенциал скоростей жидкости в упругом цилиндрическом баке определяется в виде суммы
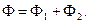
Возмущение давления жидкости на дно бака
 (45)
(45)
В дальнейшем согласно механической модели колебаний корпуса каждый тон колебаний жидкости заменяется осциллятором, закрепленном на силовом кольце. Сосредоточенные массы  на невесомых пружинах, имеющих жесткость
на невесомых пружинах, имеющих жесткость  подвешены к жестком днищам баков так, что их продольные колебания вместе с силовым кольцом для жидкости в емкости представляют переносное движение. Приведенные массы и жесткости физических маятников подсчитываются по формулам
подвешены к жестком днищам баков так, что их продольные колебания вместе с силовым кольцом для жидкости в емкости представляют переносное движение. Приведенные массы и жесткости физических маятников подсчитываются по формулам
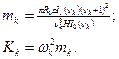
При этом масса всей жидкости в баке 
Если при решении ограничиться учетом  тонов колебаний, при подсчете параметров механической модели для всех
тонов колебаний, при подсчете параметров механической модели для всех  нужно считать
нужно считать  Массу всех осцилляторов, колебания которых не учитываются, следует отнести к распределенной массе шпангоута бака. Скалярные функции
Массу всех осцилляторов, колебания которых не учитываются, следует отнести к распределенной массе шпангоута бака. Скалярные функции  и
и  характеризующие зависимость решений краевых задач от времени в вынужденном и свободном движениях, связаны между собой коэффициентами формы
характеризующие зависимость решений краевых задач от времени в вынужденном и свободном движениях, связаны между собой коэффициентами формы 


