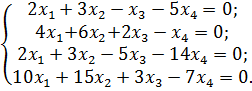Теорема 2: Сумма произведений элементов некоторой строки квадратной матрицы А на алгебраические дополнения соответствующих элементов другой строки равна нулю.
Теорема 100: Определитель, в котором все элементы одной из строк (столбцов), кроме одного, равны нулю равен произведению этого ненулевого элемента на его алгебраическое дополнение.
Пример 1 Найти определитель матрицы A:

Решение:
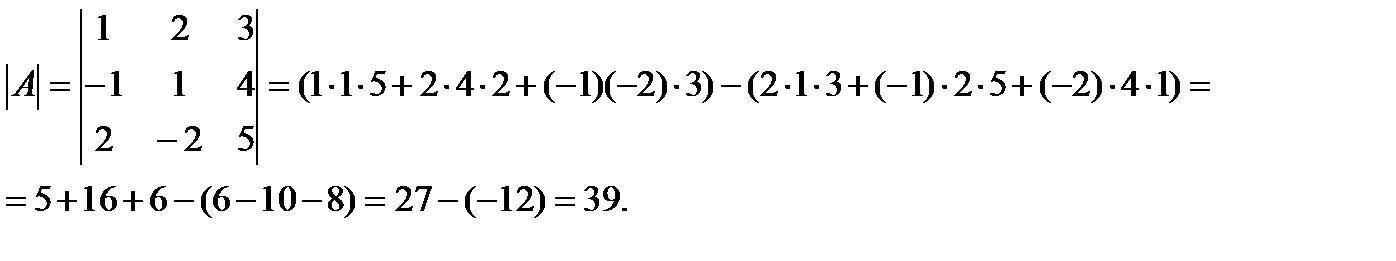
Задачи для решения
1 Найдите определитель 2-го порядка:
а)  ; б)
; б) 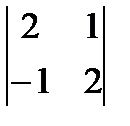 ; в)
; в) 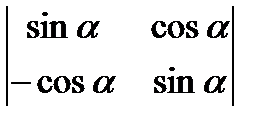 ; г)
; г)  ;
;
д)  ; е)
; е) 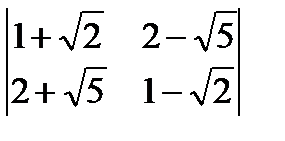 .
.
2 Найдите определитель 3-го порядка:
а)  ; б)
; б)  ; в)
; в)  ;
;
г)  ; д)
; д)  ; е)
; е) 
ж) 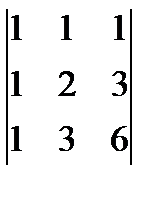 ; з)
; з)  ; и)
; и) 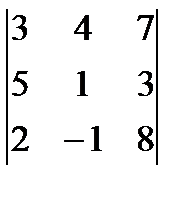 ;
;
к) 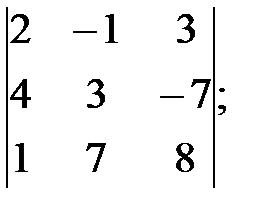 л)
л) 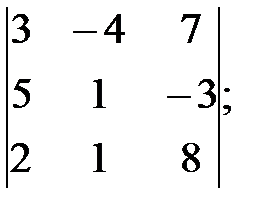 м)
м) 
3 Найдите определитель 4-го порядка:
а)  б)
б) 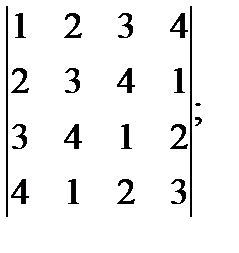 в)
в)  г)
г) 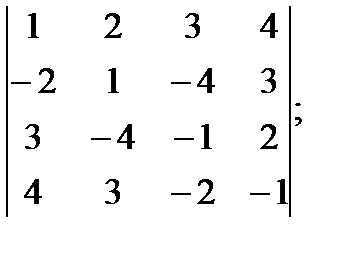
д)  е)
е) 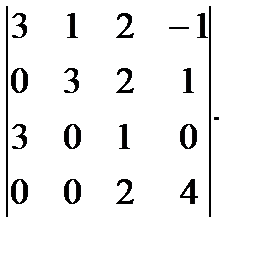
4 Найдите определитель 5-го порядка:
а)  б)
б)  в)
в) 
5 Решите уравнения, пользуясь соответствующими свойствами определителя (не применяя правило Саррюса):
а) 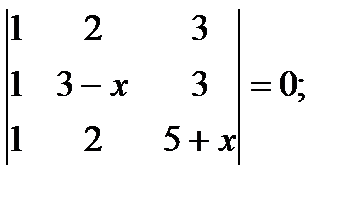 б)
б) 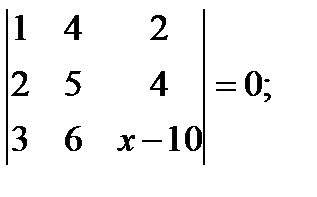 в)
в) 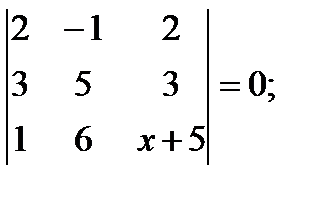
г) 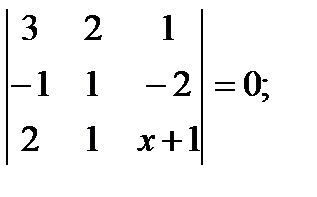 д)
д) 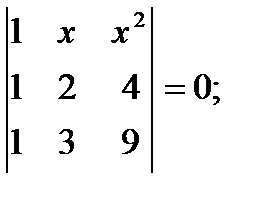 е)
е) 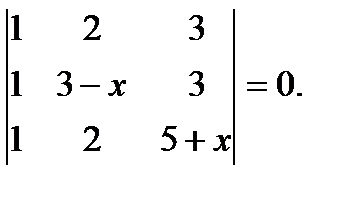
6 Вычислить определители, разложив их по элементам строки (столбца), содержащей буквы:
а)  б)
б) 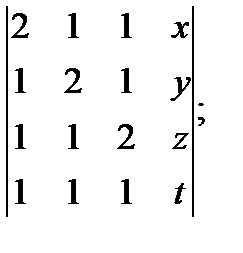 в)
в) 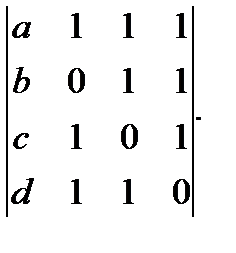
7 Путем разложения по элементам третьей строки вычислить:
а) 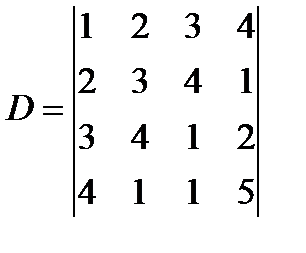 ; б)
; б) 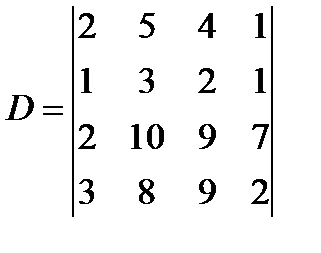 ; в)
; в) 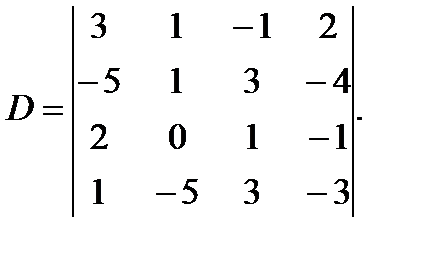
Тема 3 Обратная матрица. Вырожденные и невырожденные матрицы. Обратная матрица и ее вычисление. Матричные уравнения
Пусть A – квадратная матрица.
Матрица B называется обратной к матрице A, если 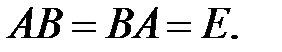
Обратная матрица обозначается A-1 и 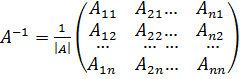 .
.
Квадратная матрица обратима тогда и только тогда, когда она невырожденная, то есть её определитель не равен нулю. Для неквадратных матриц и вырожденных матриц обратных матриц не существует.
Уравнение вида  называют простейшим матричным уравнением. Если A – квадратная невырожденная матрица, то решением такого уравнения будет матрица
называют простейшим матричным уравнением. Если A – квадратная невырожденная матрица, то решением такого уравнения будет матрица 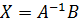 .
.
Если уравнение имеет вид 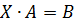 , то
, то 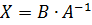 .
.
Пример 1 Найти матрицу обратную данной: 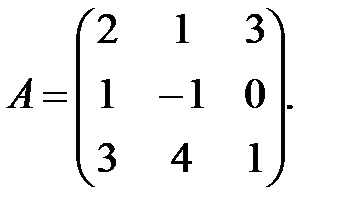
Решение
1) Найдем определитель матрицы A.

Следовательно, матрица А невырожденная и имеет себе обратную.
2) Найдем алгебраические дополнения к элементам матрицы A.
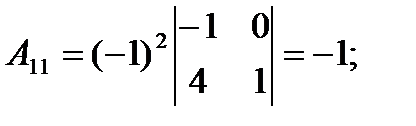

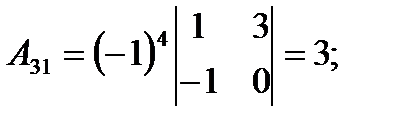
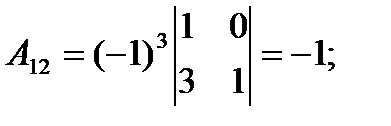
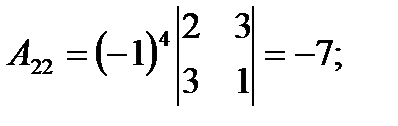
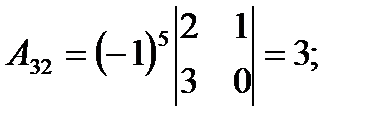
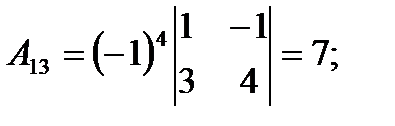
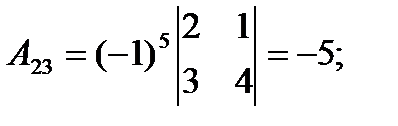
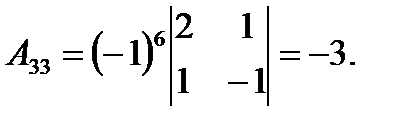
3) Запишем A-1:
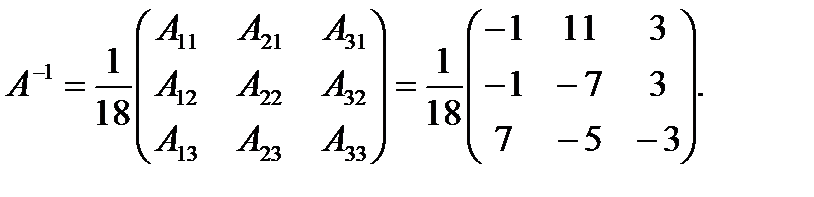
4) Выполним проверку:
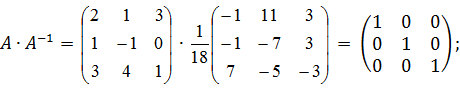
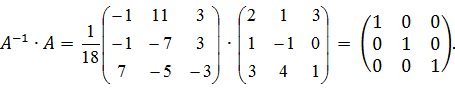
Пример 2 Решить матричное уравнение: 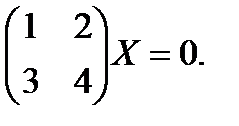
Решение
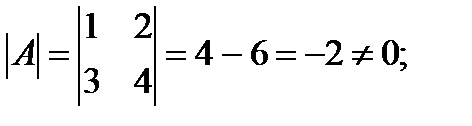

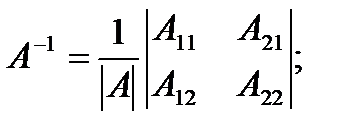

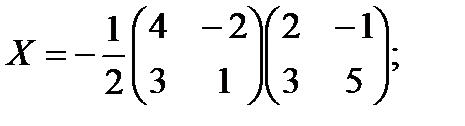

Задачи для решения
1 Найти матрицу, обратную данной:
а) 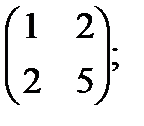 б)
б) 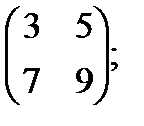 в)
в) 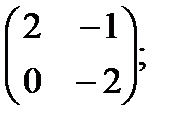 г)
г)  д)
д) 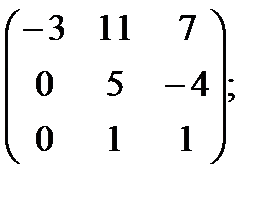
е) 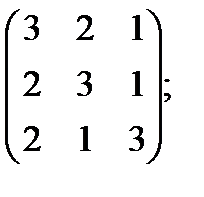 ж)
ж) 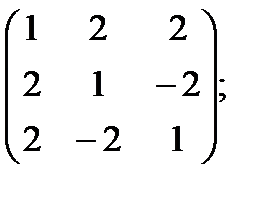 з)
з) 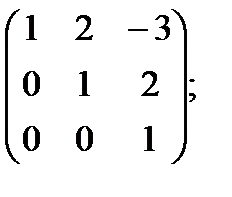 и)
и) 
к) 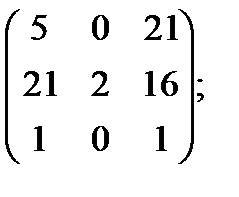 л)
л) 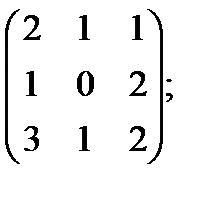 м)
м) 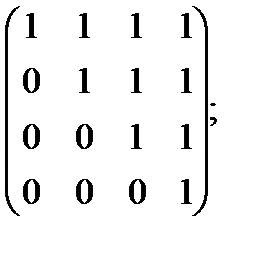 н)
н) 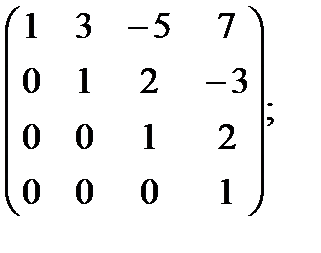
о) 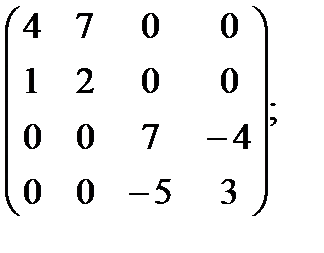 п)
п) 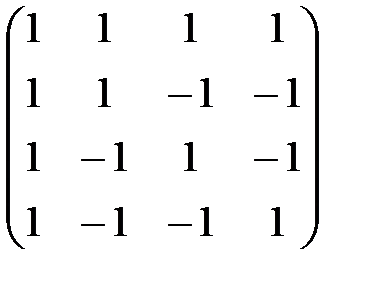 .
.
2 Решите матричное уравнение:
а) 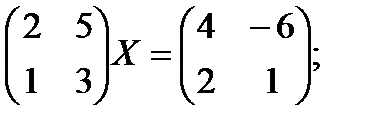 б)
б) 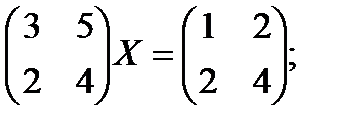
в)  г)
г) 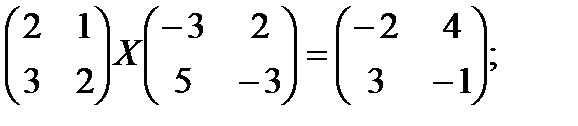
д)  е)
е) 
ж) 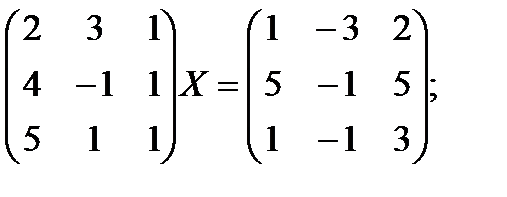 з)
з) 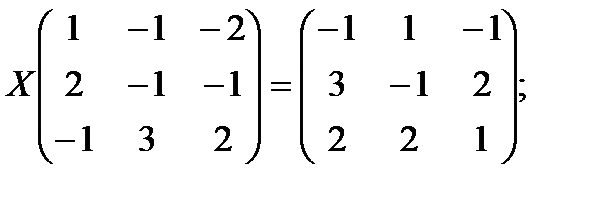
и) 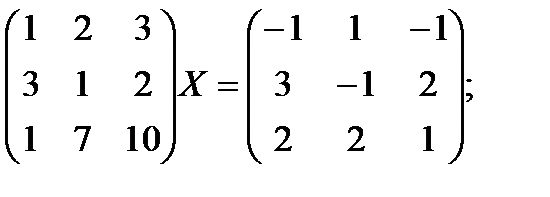 к)
к)  .
.
Раздел 3 Системы линейных уравнений. Методы решения систем линейных уравнений
Тема 1 Решение системы n – линейных уравнений с n неизвестными в матричном виде
Пусть дана система линейных уравнений:
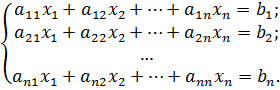
Рассмотрим матрицу, составленную из коэффициентов при неизвестных:
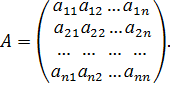
Матрица А коэффициентов при неизвестных называется главной матрицей системы.
Свободные члены и неизвестные можно записать в виде столбцевых матриц:
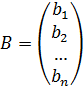
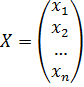
Тогда, используя правило умножение матриц, эту систему уравнений можно записать так:
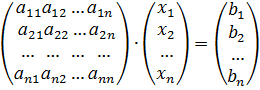
или
A·X = B (1)
Равенство (1) называется матричным уравнением или системой уравнений в матричном виде.
Отсюда
Х = 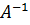 B.
B.
Таким образом, чтобы решить систему уравнение, нужно:
1) Найти обратную матрицу 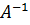 .
.
2) Найти произведение обратной матрицы 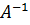 на матрицу-столбец свободных членов В, т. e. Х =
на матрицу-столбец свободных членов В, т. e. Х = 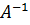 B.
B.
Пользуясь определением равных матриц, записать ответ.
Пример Решить систему уравнений:
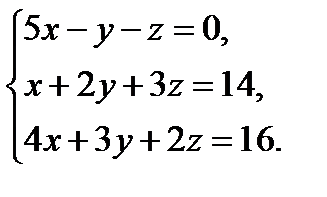
Х =  , B =
, B = 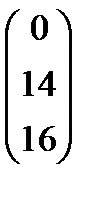 , A =
, A = 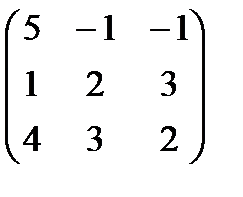
Найдем обратную матрицу А-1.
D =  =
=  5
5  2
2  2 + (-1)
2 + (-1)  3
3  4 + (-1)
4 + (-1)  1
1  3 - ((-1)
3 - ((-1)  2
2  4 + 5
4 + 5  3
3  3 + 1
3 + 1  (-1)
(-1)  2) =
2) =
= 20 - 12 - 3 - (- 8 + 45 - 2) = 5-35 = -30.
 ∙
∙ 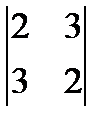 = - 5; A21 =
= - 5; A21 = 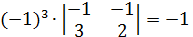 ; A31 =
; A31 = 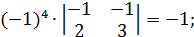
A12 = 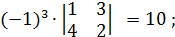 A22 =
A22 = 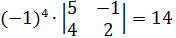 ; A32 =
; A32 =  ;
;
A13 =  ∙
∙  ; A23 =
; A23 = 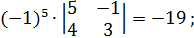 A33 =
A33 = 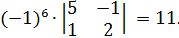
A-1 =  =
= 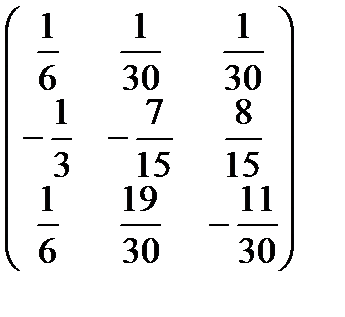 ;
;
Cделаем проверку:
A×A-1 =  =E.
=E.
Находим матрицу Х.
Х =  = А-1В =
= А-1В =  ×
×  =
=  .
.
Проверка:
 (верно)
(верно)
Решением системы является набор (1, 2, 3): x = 1; y = 2; z = 3.
Задачи для решения
1 Решить системы линейных уравнений матричным методом
а) 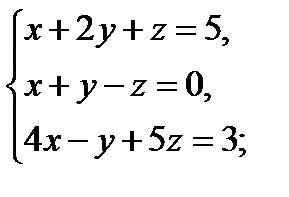 б)
б) 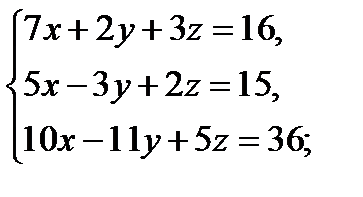 в)
в) 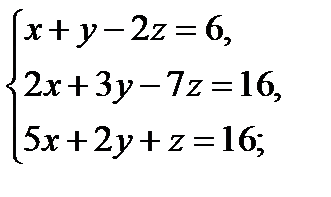
г) 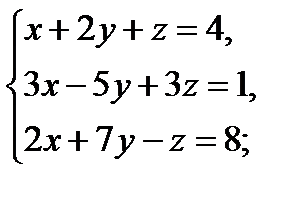 д)
д) 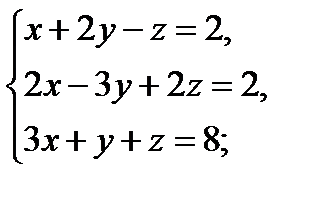 е)
е) 
2 Решить системы линейных уравнений
а)  б)
б) 
в) 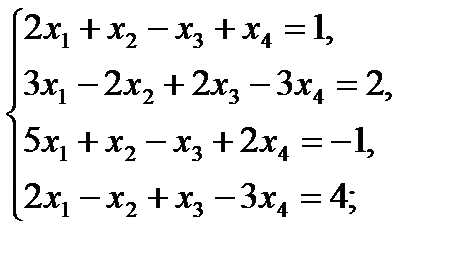 г)
г) 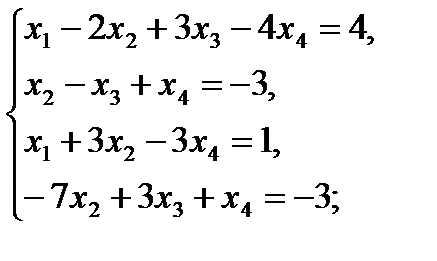
д) 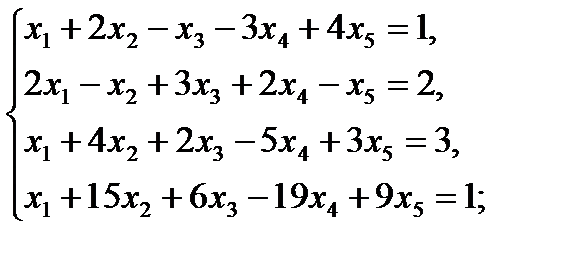 е)
е) 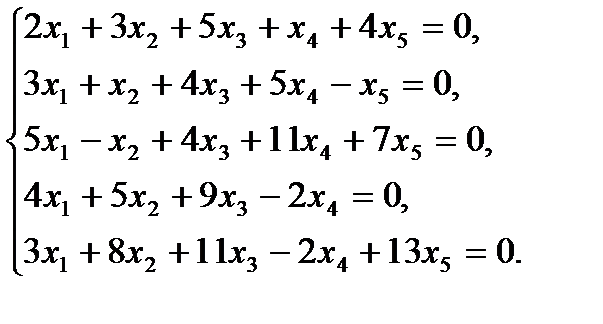
Тема 2 Правило Крамера
Рассмотрим систему n линейных алгебраических уравнений с n неизвестными
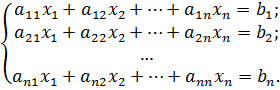
Обозначим через Δ и Δ j определитель матрицы системы и определители, полученные из определителя Δ заменой j-го столбца столбцом свободных членов системы:


Если определитель матрицы системы отличен от нуля, Δ≠0, то решение системы определяется равенствами:
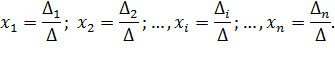
Пример Решим по правилу Крамера систему трех линейных уравнений с тремя неизвестными.
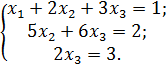
Запишем матрицу системы, столбец свободных членов и вычислим определитель матрицы системы:
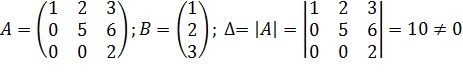 .
.
Определитель матрицы системы отличен от нуля. Система имеет единственное решение. Вычислим его по формулам Крамера. Для этого найдем определители 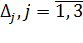 .
.
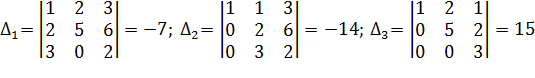 .
.
 .
.
Проверим:
 .
.
1 Решить систему линейных уравнений по правилу Крамера:
а) 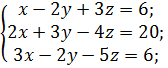 б)
б) 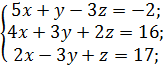 в)
в) 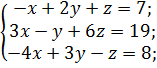
г) 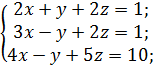 д)
д) 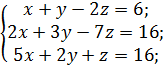 ж)
ж) 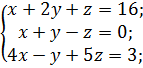
з) 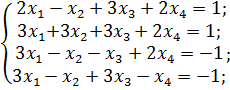 и)
и)