ЛАБОРАТОРНАЯ РАБОТА N2
"ОПТИМИЗАЦИЯ ПРОСТЕЙШЕЙ СИСТЕМЫМАССОВОГО ОБСЛУЖИВАНИЯ "
Цель работы: изучение алгоритма расчета характеристик элементарной СМО типа M/M/m/k и оптимизация характеристик неэлементарной СМО типа G/G/m/k на основе моделирования ее работы.
Постановка задачи. 1) Рассчитать аналитически характеристики функционирования простейшей СМО в соответствии с заданным вариантом.
2) Сравнить рассчитанные характеристики с аналогичными характеристиками, полученными посредством моделирования с помощью программы W:\SAIO\smo.exe.
3) Использовать программу W:\SAIO\smo.exe для оптимизации неэлементарной СМО по двум критериям:
1) по минимальному количеству обслуживающих приборов;
2) по минимальному количеству мест в накопителе;
при условиях:
1) вероятность отказа не должна превышать 0.1;
2) среднее время пребывания в очереди не должно превышать среднее время обслуживания.
3) стоимость одного места для обслуживания равна стоимости 5-ти мест для ожидания.
Порядок выполнения работы.
1. Построить аналитическую модель заданной элементарной СМО. Рассчитать аналитически следующие характеристики:
- вероятность немедленного обслуживания;
- вероятность ожидания;
- вероятность отказа;
- среднее количество заявок в системе;
- среднее время обслуживания;
- среднюю длину очереди;
- среднее время пребывания в очереди;
- среднее время пребывания заявки в системе.
2. Рассчитать аналогичные характеристики с помощью программы W:\SAIO\smo.exe. Сравнить.
3. С помощью программы W:\SAIO\smo.exe подобрать оптимальные параметры (количество обслуживающих приборов и мест в накопителе) для неэлементарной СМО.
Варианты заданий.
| № вар. | Параметры элементарной СМО | Параметры неэлементарной СМО | ||||
| К-во мест в накопителе | К-во обслуживающих прибор. | Интенсивность поступления заявок | Интенсивность обслуживания | A(t) | В(t) | |
| Треуг. прав. А=1; b=10 | Показател. l=0.05 | |||||
| Нормальный N(m=5,s=1) | Равномерн. а=10;b=30 | |||||
| Гамма l=0.5; k=3 | Треуг. лев. a=1; b=24 | |||||
| Показател. l=0.1 | Симпсона a=30; b=80 | |||||
| Равномерн. a=4; b=10 | Нормальный N(m=20, s=4) | |||||
| Треуг. лев. a=3; b=12 | Гамма l=0.1; k=6 | |||||
| Гамма l=0.4; k=4 | Нормальный N(m=50, s=10) | |||||
| Показател. l=0.2 | Треуг. прав. a=40; b=55 | |||||
| Нормальный N(m=8, s=2) | Показател. l=0.025 | |||||
| Симпсона a=5; b=15 | Равномерн. a=40; b=80 | |||||
| Треуг. лев. a=6; b=12 | Показател. l=0.01 | |||||
| Равномерн. a=3; b=13 | Гамма l=0.1; k=8 | |||||
| Треуг. прав. а=10;b=25 | Показател. l=0.015 | |||||
| Нормальный N(m=9, s=2) | Равномерн. a=30; b=70 | |||||
| Гамма l=0.5; k=4 | Показател. l=0.02 | |||||
| Показател. l=0.1 | Гамма l=0.05; k=5 | |||||
| Равномерн. a=8; b=20 | Нормальный N(m=70, s=12) | |||||
| Треуг. лев. a=5; b=11 | Треуг. прав. a=30; b=90 | |||||
| Гамма l=0.3; k=3 | Показател. l=0.02 | |||||
| Показател. l=0.3 | Равномерн. a=10; b=20 | |||||
| Нормальный N(m=11, s=2) | Симпсона a=40; b=80 | |||||
| Симпсона a=4; b=14 | Нормальный N(m=50, s=5) | |||||
| Треуг. лев. a=2; b=14 | Гамма l=0.1; k=7 | |||||
| Равномерн. a=4; b=10 | Нормальный N(m=50, s=6) | |||||
| Нормальный N(m=9, s=2) | Треуг. прав. a=10; b=100 | |||||
| Гамма l=0.5; k=4 | Показател. l=0.025 | |||||
| Показател. l=0.15 | Равномерн. a=10; b=90 | |||||
| Равномерн. a=1; b=11 | Симпсона a=20; b=80 | |||||
| Треуг. лев. a=1; b=10 | Нормальный N(m=42, s=7) | |||||
| Гамма l=0.2; k=5 | Гамма l=0.1; k=7 | |||||
| Показател. l=0.12 | Нормальный N(m=64, s=9) | |||||
| Гамма l=0.2; k=3 | Равномерн. a=40; b=80 | |||||
| Показател. l=0.2 | Симпсона а=20; b=30 | |||||
| Нормальный N(m=15, s=3) | Гамма l=0.05; k=4 | |||||
| Симпсона a=5; b=15 | Нормальный N(m=65, s=8) | |||||
| Треуг. лев. a=3; b=9 | Треуг. прав. a=30; b=90 | |||||
| Равномерн. a=2; b=14 | Показател. l=0.02 | |||||
| Нормальный N(m=7, s=1) | Равномерн. a=25; b=55 | |||||
| Гамма l=0.4; k=5 | Симпсона a=50; b=70 | |||||
| Показател. l=0.05 | Нормальный N(m=90, s=10) | |||||
| Равномерн. a=1; b=21 | Гамма l=0.1; k=6 |
3. Рекомендации к аналитическому расчету характеристик элементарной СМО.
Допустим, что в элементарной СМО m приборов, k мест в накопителе, интенсивность поступления заявок l и интенсивность обслуживания одним прибором m, рi - вероятности состояний (полученные в результате расчета).
Тогда
- среднее количество заявок в системе
N = 1×p1+2×p2+... +(m+k)×pm+k.
- среднее время обслуживания
Tоб = 1/m
- среднее время пребывания в очереди
Tож = W /(m*m)
где W = 1×pm+1+2×pm+2+... +k×pm+k - средняя длина очереди (среднее количество заявок в накопителе)
- среднее время пребывания заявки в системе
T = Tож + Tоб.
Пример. Допустим, что элементарная СМО обладает параметрами
| Количество мест в накопителе | Количество обслуживающих приборов | Интенсивность поступления заявок | Интенсивность обслуживания |
 Составим диаграмму переходов, соответствующую СМО
Составим диаграмму переходов, соответствующую СМО
Для каждого i -го состояния найдем его вероятность pi в установившимся режиме. Для этого воспользуемся формулой:
 (1)
(1)
Из (1) следует
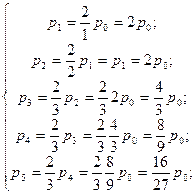 (2)
(2)
Поскольку p0+p1+p2+p3+p4+p5=1, то
 ,
,
или
p0=27/211»0.128.
Подставляя найденное значение в (2), получаем:
p1=54/211»0.256, p2=54/211»0.256, p3=36/211»0.171
p4=24/211»0.114, p5=16/211»0.076
Теперь можем найти, например,
- вероятность немедленного обслуживания Pно=p0+p1+p2=135/211»0.640;
- вероятность ожидания Pож=p3+p4=60/211»0.284;
- вероятность отказа Pотк=p5=16/211»0.076.
Остальные параметры находятся аналогичным образом.
| N | Закон распределения | P1 | P2 | K | Математическое ожидание |
| Инициализация базы генерации СВ | - | - | - | ||
| Равномерный | a | b | (a+b)/2 | ||
| Треугольный правый | a | b | (2a+b)/3 | ||
| Треугольный левый | a | b | (a+2b)/3 | ||
| Симпсона | a | b | (a+b)/2 | ||
| Показательный | l | 1/l | |||
| Гамма | l | k | k/l | ||
| Нормальный | m | s | m |
ТРЕБОВАНИЯ К ОТЧЕТУ
Отчет должен содержать:
1. Постановку задачи.
2. Аналитический расчет характеристик элементарной СМО.
3. Результаты моделирования элементарной СМО (подтверждающие правильность аналитического расчета).
4. Результаты оптимизации неэлементарной СМО (доказывающие, что подобраны оптимальные значения параметров).