ЛАБОРАТОРНАЯ РАБОТА N11
СТРУКТУРНАЯ ОПТИМИЗАЦИЯ ЛОКАЛЬНОЙ ИНФОРМАЦИОННО-ВЫЧИСЛИТЕЛЬНОЙ СЕТИ.
Цель: знакомство с методом комплексной оценки структур на примере оптимизации локальной информационно-вычислительной сети.
Постановка задачи: используя алгоритм многокритериального выбора рациональных структур найти наиболее подходящее для заданного варианта данных многопроцессорное устройство.
ИСХОДНЫЕ ДАННЫЕ
1. Множество конкурирующих структур:
S = {S1, S2, S3, S4, S5},
где Si - структура с i процессорами.
2. Совокупность частных критериев:
K = {K1, K2, K3, K4, K5},
где К1 - время ответа;
К2 - коэффициент загрузки;
К3 - пропускная способность;
К4 - вероятность правильного ответа;
K5 - стоимость процессорных устройств.
3. Матрица "критерии-структуры"
| Ед. изм. | Значе-ние кван-ты | N=10 | N=20 | |||||||||
| S1 | S2 | S3 | S4 | S5 | S1 | S2 | S3 | S4 | S5 | |||
| К1 | Сек | 0.25 | 2.89 | 2.08 | 1.83 | 1.75 | 1.72 | 5.82 | 2.85 | 2.41 | 2.15 | 1.92 |
| К2 | % | 5.0 | ||||||||||
| К3 | Зад/сек | 0.25 | 0.78 | 0.83 | 0.86 | 0.88 | 0.89 | 1.20 | 1.50 | 1.57 | 1.60 | 1.62 |
| К4 | 0.01 | 0.85 | 0.91 | 0.95 | 0.99 | 0.99 | 0.85 | 0.91 | 0.95 | 0.99 | 0.99 | |
| К5 | Млн.руб. | 50 |
| Ед. изм. | Значе-ние кван-ты | N=30 | N=50 | |||||||||
| S1 | S2 | S3 | S4 | S5 | S1 | S2 | S3 | S4 | S5 | |||
| К1 | Сек | 0.25 | 11.5 | 4.38 | 3.96 | 3.75 | 3.52 | 25.8 | 9.64 | 7.99 | 6.15 | 5.62 |
| К2 | % | 5.0 | 99.8 | |||||||||
| К3 | Зад/сек | 0.25 | 1.40 | 2.09 | 2.15 | 2.20 | 2.23 | 1.40 | 2.55 | 2.63 | 2.69 | 2.73 |
| К4 | - | 0.01 | 0.85 | 0.91 | 0.95 | 0.99 | 0.99 | 0.85 | 0.91 | 0.95 | 0.99 | 0.99 |
| К5 | млн.руб. | 50 |
| Ед. изм. | Значе-ние кван-ты | N=70 | N=100 | |||||||||
| S1 | S2 | S3 | S4 | S5 | S1 | S2 | S3 | S4 | S5 | |||
| К1 | Сек | 0.25 | 50.7 | 20.3 | 14.2 | 8.85 | 6.93 | 75.8 | 30.34 | 19.99 | 10.15 | 7.12 |
| К2 | % | 5.0 | 99.9 | |||||||||
| К3 | зад/сек | 0.25 | 1.40 | 2.75 | 3.01 | 3.19 | 3.28 | 1.40 | 2.89 | 3.34 | 3.55 | 3.75 |
| К4 | - | 0.01 | 0.85 | 0.91 | 0.95 | 0.99 | 0.99 | 0.85 | 0.91 | 0.95 | 0.99 | 0.99 |
| К5 | млн.руб. | 50 |
ВАРИАНТЫЗАДАНИЙ
|
|
| N вар | Множество конку- рирующих структур | Варинты условий функционирования и их вероятности |
| S1,S2,S3 | N = 10, 20, 30; p(N)=0.5,0.3,0.2 | |
| S2,S3,S4 | N = 10, 20, 30; p(N)=0.4,0.4,0.2 | |
| S3,S4,S5 | N = 10, 20, 30; p(N)=0.1,0.5,0.4 | |
| S1,S2,S3 | N = 20, 30, 50; p(N)=0.2,0.7,0.1 | |
| S2,S3,S4 | N = 20, 30, 50; p(N)=0.3,0.4,0.3 | |
| S3,S4,S5 | N = 20, 30, 50; p(N)=0.4,0.5,0.1 | |
| S1,S2,S3 | N = 30, 50, 70; p(N)=0.1,0.4,0.5 | |
| S2,S3,S4 | N = 30, 50, 70; p(N)=0.2,0.6,0.2 | |
| S3,S4,S5 | N = 30, 50, 70; p(N)=0.1,0.3,0.6 | |
| S1,S2,S3 | N = 50, 70,100; p(N)=0.3,0.3,0.4 | |
| S2,S3,S4 | N = 50, 70,100; p(N)=0.2,0.4,0.4 | |
| S3,S4,S5 | N = 50, 70,100; p(N)=0.5,0.3,0.2 | |
| S1,S3,S5 | N = 10, 20, 30; p(N)=0.1,0.5,0.4 | |
| S1,S3,S5 | N = 20, 30, 50; p(N)=0.4,0.3,0.3 | |
| S1,S3,S5 | N = 30, 50, 70; p(N)=0.2,0.3,0.5 | |
| S1,S3,S5 | N = 50, 70,100; p(N)=0.1,0.2,0.7 | |
| S1,S2,S4 | N = 10, 20, 30; p(N)=0.1,0.5,0.4 | |
| S1,S2,S4 | N = 20, 30, 50; p(N)=0.2,0.3,0.5 | |
| S1,S2,S4 | N = 30, 50,70; p(N)=0.2,0.7,0.1 | |
| S1,S2,S4 | N = 50, 70,100; p(N)=0.3,0.4,0.3 | |
| S2,S4,S5 | N = 10, 20, 30; p(N)=0.2,0.5,0.3 | |
| S2,S4,S5 | N = 20, 30, 50; p(N)=0.3,0.3,0.4 | |
| S2,S4,S5 | N = 30, 50,70; p(N)=0.2,0.6,0.2 | |
| S2,S4,S5 | N = 50, 70,100; p(N)=0.3,0.3,0.4 | |
| S2,S3,S5 | N = 30,50,70; p(N)=0.1,0.4,0.5 |
ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Методика многокритериального выбора рациональных структур.
Рассмотрим методику, которая реализует все операторы метода комплексной оценки структур.
Этап 1. Определяется множество конкурирующих структур
{ Si} = { S1, S2, … Sn },
из числа которых выбирается в дальнейшем рациональная структура. Для поиска структур могут быть использованы различные методы – «мозговой атаки», «дерева целей», «морфологического ящика» и др. Морфологический анализ создаваемой системы позволяет систематизировать потенциально возможные структуры и определить множество конкурирующих структур.
|
|
Этап 2. Отбирается совокупность частных критериев
{ Кj} = { K1, K2, … Km },
которые служат для оценки конкурирующих структур. К набору критериев предъявляется ряд требований:
1) полнота, т.е. набор критериев должен охватывать все важные аспекты решаемой задачи;
2) операциональность, т.е. каждый критерий должен характеризовать вполне определенное свойство системы;
3) измеримость, т.е. каждый критерий должен допускать оценку интенсивности характеризуемого им свойства;
4) декомпозируемость, т.е. критерии набора должны обеспечить возможность разложения задачи на части с меньшей размерностью;
5) неизбыточность, т.е. критерии набора не должны учитывать один и тот же аспект последствий;
6) минимальность, т.е. набор критериев должен содержать как можно меньшее число критериев.
Противоречивость требований заставляет искать компромисс при построении набора критериев.
Этап 3. Выполняется оценка конкурирующих структур по частным критериям для m -го варианта условий 
. Для оценки структур используются все возможные средства, которые имеются в наличии на данный момент эволюции системы: аналитические, имитационные, полунатурные модели; натурные испытания; проведение экспертиз. Получаемые оценки 
образуют матрицу «критерии-структуры» (табл. 1):
Таблица 1.
| { Kj} | Единица измерения | Направление экстремума | {Si} | |||
| S1 | S2 | … | Sn | |||
| K1 | 
| 
| … | 
| ||
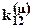
| K2 | 
| 
| … | 
| ||
| … | … | … | … | … | … | … |
| Km | 
|
| … | 
|
Этап 4. Составляется матрица бинарных предпочтений ЛПР, которая содержит результаты попарных сравнений критериев по важности: «1» - если критерий строки считается более важным, чем критерий столбца; «0» - в противном случае («0,5» - если критерии не сравнимы по важности). Суммирование оценок по строке определяет «цену» критерия 
(табл. 2):
|
|
Таблица 2.
| { Kj} | K1 | K2 | … | Km |
|
| K1 | … | 
| |||
| K2 | … | 
| |||
| … | … | … | … | … | |
| Km | … | 
|
Этап 5. Находятся веса частных критериев, отражающие неформальные предпочтения ЛПР:
.
Этап 6. Находятся веса частных критериев, исходя из разброса векторных оценок:
.
Здесь 
,
где 
.
Этап 7. Находятся усредненные веса, характеризующие важность частных критериев:
где
Этап 8. Оценки матрицы «критерии-структуры» приводятся к безразмерному виду
где 
значение «кванты» по частному критерию Kj, причем под квантой понимается мера разумной точности измерения соответствующей характеристики.
Этап 9. Формируется матрица мер эффективности
Этап 10. Вычисляются обобщенные скалярные оценки
т.е. находится разность суммарных мер эффективности по критериям, подлежащим соответственно максимизации и минимизации.
Этап 11. При оценке структур в диапазоне условий осуществляется h- кратное повторение этапов 3-10. В результате получаем матрицу «структуры-условия» (табл. 3.):
Таблица 3.
| { Sj} | { m } | |||
| … | h | |||
| S1 |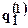 
| 
| … | 
|
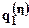
| S2 | 
| 
| … | 
|
| … | … | … | … | … |
| Sn | 
| 
| … | 
|
Этап 12. На основе матрицы «структуры-условия» выбирается рациональная структура системы. Эта структура должна обладать приемлемой эффективностью для всех вариантов условия, возникающих с вероятностями pm. Для известных вероятностей pm, имеющих частотную или субъективную трактовку, целесообразно использовать критерий максимума средней эффективности в диапазоне условий:
На практике типичной является ситуация, когда вероятности pm неизвестны. В данном случае используются критерии для выбора решений в условиях неопределенности.
Замечание. Методика может быть использована как в полном объеме, так и в усеченных вариантах.