Лекция № 1 / 10 семестр.
Тема: Планирование и организация ТО АТ с использованием математических методов. (с 158.)
Время: 2 часа.
Учебные вопросы: 1. Задачи решаемые с помощью теории массового обслуживания.
Поток требований на техническое обслуживание.
Задачи решаемые с помощью теории массового обслуживания.
В подавляющем большинстве областей человеческой деятельности встречаются процессы, носящие характер массового обслуживания. Это относится к бытовому обслуживанию, торговле, транспорту, экономике, снабжению, производству, медицине и т. п.
В понятие «обслуживание» вкладывается широкое содержание, т. е. удовлетворение потребностей. Применительно к гражданской авиации — это продажа билетов и авиационные перевозки, применение авиации в сельском хозяйстве, техническое обслуживание и ремонт авиационной техники, организация опорных баз выполнения периодического технического обслуживания и т. п. Во всех указанных областях деятельности гражданской авиации речь идет об удовлетворении спроса на большой поток заявок (требований). Планирование и организация процесса удовлетворения такого рода требований успешно решаются методами теории массового обслуживания.
Они позволяют на базе использования математического аппарата, а в последнее время и вычислительной техники, находить наиболее оптимальные решения.
Каждое поступившее требование нуждается в обслуживании со стороны какого-либо устройства, либо человека, либо группы людей (бригады). Средства, которые осуществляют обслуживание требований, называют обслуживающими аппаратами. На практике, как правило, приходится иметь дело не с одним, а с группой обслуживающих аппаратов Совокупность аппаратов, призванных обслу 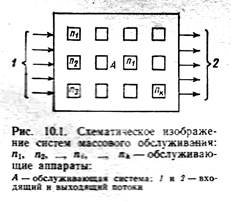 живать однородные требования, принято называть обслуживающей системой.
живать однородные требования, принято называть обслуживающей системой.
|
|
Процесс массового обслуживания протекает по одному и тому же принципу: требования на обслуживание поступают в обслуживающую систему, обрабатываются обслуживающими аппаратами и покидают ее (рис. 10.1). Поток требований, нуждающихся в обслуживании и поступающих в обслуживающую систему, называют входящим потоком. Поток требований. покидающий обслуживающую систему, называют выходящим потоком.
В большинстве задач массового обслуживания входящий поток требований находится в зависимости от многих случайных факторов, и поэтому его трудно регулировать и определять заранее число требований в заданный промежуток времени.
Поэтому входящий поток обычно описывается с помощью вероятностных характеристик.
От того же сколько успешно будут решены организационные вопросы, будет зависеть качество функционирования обслуживающей системы, что в свою очередь оценивается полнотой загруженности системы, продолжительностью ожидания начала обслуживания, длиной очереди, стоимостью обслуживания.
Задачей теории массового обслуживания является отыскание зависимостей величин, характеризующих качество функционирования обслуживающей системы, от характеристик входящего потока, возможностей обслуживающих аппаратов и способов организации работы обслуживающей системы.
Поток требований на техническое обслуживание.
Под потоком требований, как упоминалось выше, понимают совокупность заявок на обслуживание, поступающих в обслуживающую систему. Изучение потока требований является первой и необходимой задачей при практическом использовании теории массового обслуживания. Это тем более важно, что его надо уметь описать количественно.
|
|
Процессу технического обслуживания летательных аппаратов свойственны элементы случайности. Отмены и задержки рейсов, отказы и неисправности авиационной техники, недостатки в обеспечении запасными частями, выполнение доработок и разовых осмотров и другие причины вызывают нерегулярность поступления летательных аппаратов на техническое обслуживание и непостоян
 В данном случае -под требованием понимается летательный аппарат, нуждающийся в техническом обслуживании, под обслуживающим аппаратом — бригаду, средства механизации, а под системой массового обслуживания —АТБ.
В данном случае -под требованием понимается летательный аппарат, нуждающийся в техническом обслуживании, под обслуживающим аппаратом — бригаду, средства механизации, а под системой массового обслуживания —АТБ.
Поэтому для решения практических задач во многих случаях принимают простейший поток, удовлетворяющий условиям стационарности; ординарности и отсутствия последействия.
Стационарность потока означает, что интенсивность потока требований в течение рассматриваемого периода постоянна. Ординарность потока выражает собой практическую невозможность появления двух и более требований за достаточно малый промежуток времени, т. е. одновременно может поступить не более одного требования на обслуживание. Отсутствие последействия (взаимозависимости) означает, что число требований, поступивших в систему после произвольного момента времени t, не зависит от того, какое число требований поступило в систему до момента t, т. е. взаимонезависимо. Потоки, удовлетворяющие этим условиям, называются пуассоновскими.
|
|
Вероятность поступления n требований простейшего потока за время t вычисляется по формуле Пуассона
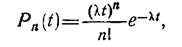
|
где 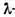 —среднее число требований на обслуживание, поступающих за единицу времени (интенсивность потока).
—среднее число требований на обслуживание, поступающих за единицу времени (интенсивность потока).
Интенсивность потока с течением времени может не оставаться постоянной. Например, интенсивность потока требований на обслуживание летательных аппаратов днем больше, чем ночью. Поэтому и организация обслуживания, являющаяся оптимальной при данной интенсивности потока требований, не будет оптимальной при другой интенсивности. В связи с этим для правильной организации обслуживания необходимо выделять периоды с одинаковой интенсивностью потока и решать возникающие задачи для каждого из них.
На рис. 10.2 представлен график суточной интенсивности вылетов в одном из аэропортов. Из графика видно, что имеются два периода, в каждом из которых интенсивность потока можно считать постоянной: первый период —с 7 до 21 ч и второй — с 21 до 7 ч. Ясно, что работа аэропорта в эти периоды должна быть организована по-разному.
 В практике часто встречаются потоки требовании с ограниченным последействием. Это означает что момент появления очередного требования зависит толькоот того, когда поступило предыдущее, и не зависит от того, как чередовались требования ранее. В этом смысле влияние всего потока на момент появления очередного требования ограничено только последним требованием. Такие потоки обозначаются символом GI.
В практике часто встречаются потоки требовании с ограниченным последействием. Это означает что момент появления очередного требования зависит толькоот того, когда поступило предыдущее, и не зависит от того, как чередовались требования ранее. В этом смысле влияние всего потока на момент появления очередного требования ограничено только последним требованием. Такие потоки обозначаются символом GI.
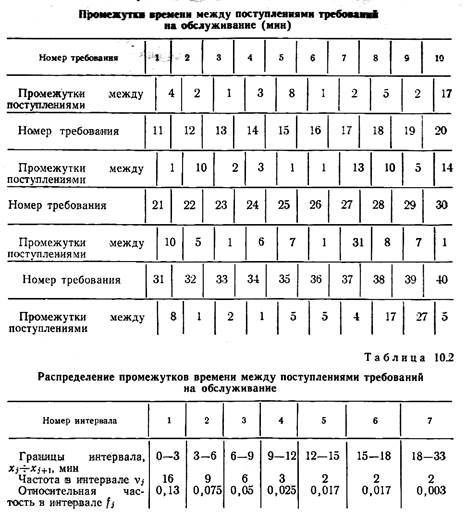
Промежутки времени между последовательными поступлениями требований являются случайными величинами. Для полного описания их необходимо указать не только среднюю длину промежутков, но и распределение промежутков, т. е. указать, как часто они принимают те или иные числовые значения.

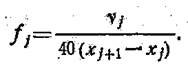
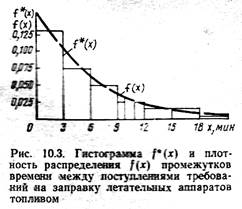
Отложив на оси абсцисс (рис. 10.3) границы интервалов, а на оси ординат — относительные частости, построим в этих координатах гистограмму 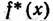 по формуле
по формуле
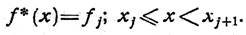
Эта гистограмма дает наглядное представление о распределении промежутков времени между поступлениями требований на обслуживание. Сгладим ступенчатую гистограмму непрерывной кривой f(x). При достаточно малом значении 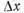 площадь
площадь 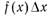 равна вероятности того, что время между поступлениями требований находится в интервале от х до
равна вероятности того, что время между поступлениями требований находится в интервале от х до 
Функция f(х) называется плотностью распределения рассматриваемой случайной величины. Она определяет закон распределения, так как показывает, с какой вероятностью эта величина принимает те или иные значения. Представленная гистограмма хорошо сглаживается экспоненциальной кривой, поэтому можно
считать, что промежутки времени между поступлениями требований на заправку самолетов топливом имеют экспоненциальное распределение, и описываются формулой
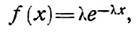
где 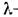 —параметр распределения, равный среднему числу требований, поступающих на обслуживание за единицу времени.
—параметр распределения, равный среднему числу требований, поступающих на обслуживание за единицу времени.
|
В рассмотренном выше примере среднее время между поступлениями равно 6 мин. Следовательно, 
Если промежутки времени между появлениями требований распределены по экспоненциальному закону, то даже знание того, сколько времени прошло с момента появления последнего требования, не дает дополнительной информации о моменте появления очередного. Это поток без последействия. Всякий ординарный стационарный поток без последействия является пуассоновским. Его обозначают символом М. В рассматриваемом примере с топливозаправщиками требования на заправку самолетов топливом образуют пуассоновский поток. В частном случае может иметь место поток, в котором требования появляются" через постоянные промежутки времени. Знание момента появления очередного требования позволяет совершенно точно определить момент появления следующего. Такой поток называют д е т е р м я н и р о в а н н ы м и обозначают символом D.
В потоках с ограниченным последействием интервалы времени между поступлениями требований непостоянны и не распределены экспоненциально. О виде распределения можно судить по гистограмме.
Показателем случайности или, наоборот, регулярности потока может служить среднее квадратическое отклонение промежутков времени между поступлениями требований: 

где 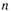 —общее число промежутков; —общее число промежутков; 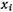 —зарегистрированные значения промежутков; —зарегистрированные значения промежутков; 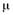 —среднее значение промежутков: —среднее значение промежутков:
|
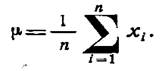
Среднее квадратическое отклонение о является мерой разброса рассматриваемой случайной величины около ее среднего значения. Если поток чисто случайный, т. е. если промежутки времени между поступлениями требований распределены экспоненциально, то 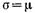 (разброс велик). Если поток детерминированный, то
(разброс велик). Если поток детерминированный, то 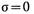 (разброса нет). Для потоков промежуточного типа значение о больше нуля и, как правило, меньше
(разброса нет). Для потоков промежуточного типа значение о больше нуля и, как правило, меньше 
Контрольные вопросы
1. Укажите область применения теории массового обслуживания в ГА какие задачи она призвана решать. Дайте понятие о обслуживающей системе.
2. Какими характеристиками должен обладать поток требований на обслуживание в системе обслуживающих аппаратов (в теории массового обслуживания) применительно к процессу обслуживания ЛА ГА. Формула Пуассона.
3 Как характеризуют поток требований свойства Ординарности, Стационарности, и Отсутствие последействия. в теории массового обслуживания применительно к ТО ЛА ГА.