Тестовые задания с выбором одного правильного ответа

МАТЕМАТИКА

Методические рекомендации к выполнению заданий

Тестовые задания с выбором одного правильного ответа

1. Исключите иррациональность в знаменателе: .

A)

B)

C)

D)

E)

Решение: Умножаем числитель и знаменатель дроби на выражение сопряженное знаменателю

Ответ: А)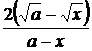

2. Решите неравенство:

A)

B)

C)

D)

E)

Решение: Так как , неравенство выполняется при любом х взятого из области определения

Ответ: С)

3. Преобразуйте в произведение:

A)

B)

C)

D)

E)

Решение: Воспользуемся формулой

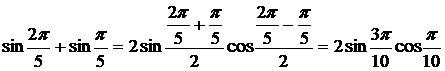
Ответ: B)

 

4. Найдите х, если известно, что числа (-1); х+2; sin(arcsin x ), взятые в указанном порядке образуют геометрическую прогрессию.

A) x = -1, x = -4

B) x = -4

C) x = -2, x = -4

D) х = 1

E) х = -1

Решение:

Для начала необходимо помнить, что sin(arcsinx)=х, если хϵ

поэтому значения х могут быть только из отрезка

Если числа (-1); х+2; sin(arcsin x ), образуют геометрическую прогрессию, то используя характеристическое свойство этой прогрессии, имеем

в ² = в ∙ в , где в = - 1; в = х + 2; в = sin(arcsinx).

(x + 2) = - 1 ∙ sin(arcsinx).

x²+ 4x + 4 = - x

x² + 5x + 4 = 0, x = -1, x = -4

Как было указано выше, хϵ , х = -1

Ответ: Е) х = -1

 

5. Найдите угловой коэффициент касательной к графику функции в точке с абсциссой

A)

B) 4

C)

D)

E)

Решение:

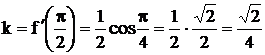
Ответ: D)

6. В первом и втором сплавах медь и цинк находятся соответственно в соотношении 5:2 и 3:4. Сколько кг каждого сплава нужно взять, чтобы получить 28 кг нового сплава с равным содержанием меди и цинка?

A) 6 кг и 20 кг

B) 5 кг и 19 кг

C) 7 кг и 21 кг

D) 4 кг и 18 кг

E) 7 кг и 20 кг

 

Решение:

Пусть из первого сплава нужно взять х кг, а из второго у кг. Тогда масса меди в новом сплаве равна 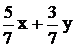, масса цинка . Получаем:

Ответ: C) 7 кг и 21 кг

 

7.Сотовый оператор предлагает три тарифных плана в роуминге.

№ п/п	Тарифный план	Абонентская плата	Дополнительная оплата
1.	Лёгкий старт	$1 в день	При общем разговоре свыше 0,5 часа в день взимается плата по $0,09 за минуту
2.	Деловой	$4,7 в день	При общем разговоре свыше 1,5 часа в день взимается плата по $0,08 за минуту
3.	Свобода общения	$5 в день	При общем разговоре свыше 1 часа в день взимается плата по $0,05 за минуту

Какой тариф будет наиболее выгоден абоненту если он в день будет разговаривать по 2,5 часа на протяжении 15 дней?

A) 1

B) 2

C) 1 и 3

D) Невозможно определить

E) 3

Решение:

При решении задачи следует учесть, что дополнительная плата взимается со всего времени разговора. (В условии сказано: при общем разговоре свыше указанных часов по тарифным планам в день взимается дополнительная соответствующая плата за минуту).

мин

Общая сумма за 15 дней по тарифному плану №1:

Общая сумма за 15 дней по тарифному плану №2:

Общая сумма за 15 дней по тарифному плану №3:

Таким образом, наиболее выгоден тариф № 3.

Ответ: E) 3

 

8. Составьте приведенное квадратное уравнение, имеющие корни х₁=3,

х₂= –1

A)

B)

C)

D)

E)

Решение: По теореме Виета:

Тогда уравнение имеет вид:

Ответ: A)

 

9. Первый и четвертый члены геометрической прогрессии равны 3 и 81 соответственно. Найдите знаменатель прогрессии q.

A) 3

B) 4

C) 5

D) 6

E) 7

Решение:

Ответ: A) 3

 

10. Решите уравнение:

A)

B)

C) 3

D)

E) – 3

Решение:

ОДЗ:

 

 

Ответ: B)

11. К стороне параллелограмма, равной 20 см проведена высота длиной 14 см. Найдите другую сторону, если высота, проведенная к ней равна 28 см.

А) 20 см

В) 15 см

С) 10 см

D) 14 см

Е) такого параллелограмма не существует.

Решение

С

В

:

 

 

Используем формулу площади параллелограмма S=a·h . Имеем,

S=20·14= СД·28, тогда СД= АВ=10 см.

Геометрическая интерпретация результата показывает, что данная задача не имеет решения, так как не существует прямоугольного треугольника с гипотенузой 10 см и катетом 14 см.

Ответ: Е) такого параллелограмма не существует.

 

12. В магазине есть 6 сортов колбасы и 5 видов шоколадок. Покупателю требуется приобрести 2 куска колбасы разных сортов и 3 шоколадки разного вида. Тогда количество способов составления данной покупки равно

A) 85

B) 150

C) 115

D) 75

E) 120

Решение:

Выбрать 2 сорта колбасы из 6 имеющихся в магазине можно способами.

Выбрать 3 шоколадки из 5 предложенных видов можно способами.

По правилу умножения имеем вариантов составления покупки. Используем формулу:

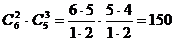
Ответ: B) 150

 

13. Пельмени различных фирм продают в упаковках:

 

Вес упаковки пельменей	450 г	500 г	700 г	900 г	1200 г
Стоимость упаковки	540 тг	450 тг	710 тг	880 тг	1300 тг

 

Покупатель выбрал самую выгодную упаковку. За две упаковки пельменей покупатель заплатит:

А) 1100 тг

В) 900 тг

С) 1080 тг

D) 1420 тг

E) 1300 тг

Решение:

Рассчитаем стоимость 100 г пельменей каждого сорта. Для этого необходимо, стоимость упаковки разделить на его вес и умножить на 100г:

 

1) тг за 100 г продукта

2) тг за 100 г продукта

3) тг за 100 г продукта

4) тг за 100 г продукта

5) тг за 100 г продукта

Следовательно, самая выгодная упаковка стоит 90 тг за 100 г.

Значит 2*500 г=1 кг будет 900 тг

 

Ответ: В) 900 тг

 

14. По данным квитанции (см.таблицу) семья Ахметовых, состоящая из 3-х человек, заплатит за электроэнергию

 

Начальные показания (кВТ)	Конечные показания (кВТ)	Тариф	Стоимость тарифа (тг)	Кол-во на 1 человека (1 кВТ/ч)	Начислено
		1 уровень	8,6	0-90
2 уровень	11,2	90-180
3 уровень	13,9	свыше
Итого

A) 3890 тг

B) 2322 тг

C) 1568 тг

D) 3880 тг

E) 2322 тг

Решение:

По показаниям счетчика высчитываем кВт, потраченные за месяц семьей.

1) 3150-2740=410 кВт, тариф 1 уровня на человека 90 кВт, следовательно по первому тарифу оплачивать 270 кВт.

2) 410-270=140 кВт, семья оплачивает по 2-му уровню, который на человека позволяет тратить 90-180 кВт.

3) 270*8,6+140*11,2=2322+1568=3890 тг

Семье необходимо заплатить за электроэнергию 3890 тг.

Ответ: А) 3890 тг

 

15. Две стороны треугольника равны 7 см и 8 см, синус угла между ними равен . Найдите третью сторону треугольника, если она наибольшая из сторон данного треугольника.

A) или

B) или

C) или

D) или

E) или

 

В

Решение:

 

 

С

8см

 

 

Если sin = , то cos ² =1- sin ² = 1- = 1 - =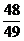

cos = или cos = -

- острый угол - тупой угол

По теореме косинусов

BC² = AB² + AC² - 2AB ∙ AC ∙ cos

1) Если - острый, то BC²=7² + 8² - 2 ∙ 7 ∙ 8 ∙ = 97

BC =

2) Если - тупой, то BC² = 7² + 8² - 2 ∙ 7 ∙ 8 ∙ = 129

BC =

Ответ: D) или

 

16. Диагональ куба равна 3. Найдите площадь полной поверхности куба

A) 14

B) 18

C) 16

D) 20

E) 15

 

Решение:

Так как гранями куба являются квадраты, то площадь полной поверхности равна:

 

Ответ: B) 18

 

17. В коробке лежат 23 шара: красные, белые и черные. Белых шаров в 11 раз больше, чем красных. Сколько черных шаров?

A) 10

B) 11

C) 12

D) 13

E) 14

Решение: Допустим, в коробке 1 красный шар. Тогда белых будет 11, а черных 23-(11+1)=11. Если в коробке 2 красных шара, тогда белых будет 22; 22+2>23.

Ответ: B) 11

 

18. Куб с ребром 6 см составлен из маленьких кубиков с ребром 1 см. Сколько нужно удалить кубиков, убрав внешний слой, состоящий из маленьких кубиков.

A) 115

B) 125

C) 152

D) 112

E) 136

Решение:

Внешний слой состоит из верхней, нижней и четырех боковых граней 6×6.

Удаляем верхнюю грань 6×6 = 36 маленьких кубиков.

В двух противолежащих гранях осталось по 5×6 = 30.

После их удаления в двух других противолежащих гранях осталось по 5×4 = 20 маленьких кубиков.

После их удаления в нижней грани осталось 4×4 = 16.

Таким образом, всего необходимо удалить 36 + 30·2 + 20·2 + 16 = 152 маленьких кубика.

Ответ: C)152

 

19. В равнобедренной трапеции острый угол равен , а высота в 3 раза меньше большего основания. Найдите площадь трапеции, если меньшее основание равно 6 см.

A) 52 см²

B) 36 см²

C) 27 см²

D) 62 см²

E) 72 см²

Решение:

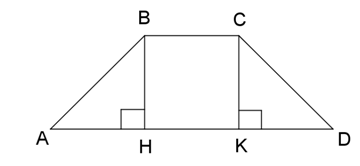
равнобедренный.

По условию

; см²

Ответ: C) 72 см²

 

20. Числа внутри рисунка получены по определенному закону арифметических действии. Какое число должно быть вместе? знака.

 

A) 45

B) 40

C) 36

D) 34

E) 32

Решение: Задание логического характера. Здесь наблюдается следующая закономерность: Следовательно,

Ответ: D) 34

 

21. Упростите выражение: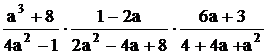

A)

B)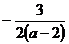

C)

D)

E)

F)

G)

H)

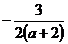Решение: Ответ: A) , G)

22. Решите уравнение:

A) 0

B) 1

C) 2

D) 3

E) –2

F) 4

G) –3

H) –1

Решение:

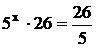
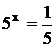
х= –1

Ответ: H) –1

23. Решите неравенство:

A)

B)

C)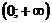

D)

E)

F)

G)

H)

Решение: неравенство выполняется для любого х, т.к.

Ответ: A)

 

24. Известно, что При каких значениях х,

A)

B)

C)

D)

E) 5

F) 3

G)

H)

Решение:

Ответ: A) , B)

25. Решите уравнение:

A) 6; 3; 2; 1

B) – 6; 3; – 2; 1

C) – 6; –3; 2; 1

D) – 6; –3; – 2; 1

E) 6; –3; – 2; 1

F) – 6; –3; – 2; – 1

G) 6; –3; 2; 1

H) 6; 3; – 2; 1

Решение:

 

 

Так как в правой части уравнения находится положительное число, то данное уравнение равносильно следующей совокупности уравнений:

и

 

Ответ: D) – 6; –3; – 2; 1

26. Решите уравнение:

A) 2

B) 6

C)

D)

E) 11

F)

G)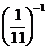

H)

Решение: , ОДЗ:

Ответ: A) 2, C)

27. Решите систему неравенств:

A)

B)

C) ,

D) ,

E) ,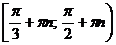

F) (),

G) ,

H) ,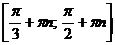

Решение:

Ответ: B)

28. Найдите производную функции

A)

B)

C)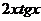

D)

E)

F)

G)

H)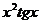

Решение:

Ответ: A)

29. В конусе образующая равна 4 и наклонена под углом 60⁰. Найдите объем конуса.

A)

B)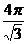

C)

D)

E)

F)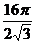

G)

H)

Решение:

 

Ответ: A) , F) , H)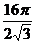

30. От одной и той же платформы в противоположных направлениях отошли два электропоезда. Скорость одного из них 70 км/ч, а другого 80 км/ч. Через сколько часов расстояние между ними будет 600 км?

A) 3 ч

B) 2 ч

C) 5 ч

D) 6 ч

E) 7 ч

F) 4 ч

G) 0,5 ч

H) 3,5 ч

Решение:

Пусть х ч.– время движения, тогда

70х+80х=600

150x=600

x=4

Ответ: F) 4 ч