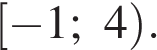Решение.
Областью определения неравенства являются положительные числа, отличные от 0,25 и 1. Выражение 
либо равно нулю при 
при этом неравенство верно; либо положительно, и тогда на него можно разделить, не меняя знака неравенства. Имеем:
Учитывая, что 
, получаем ответ: 
Ответ:
Критерии проверки:
Источник: РЕШУ ЕГЭ — Предэкзаменационная работа 2014 по математике.
Решение.
Заметим, что в ОДЗ данного неравенства входят все положительные числа за исключением 
Преобразуем неравенство:
Сделаем замену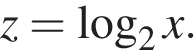 
Откуда получаем:
Ответ: 
Критерии проверки:
Задание 15 № 508504
Решите неравенство: 
Решение.
Заметим, что в ОДЗ данного неравенства входят все положительные числа за исключением Преобразуем неравенство:
Сделаем замену 
имеем:
Тогда 
или 
откуда получаем множество решений неравенства: 
Ответ:
Критерии проверки:
Задание 15 № 508506
Решите неравенство: 
Решение.
Преобразуем неравенство: 
Рассмотрим два случая. Первый случай: 
Откуда, учитывая условие 
получаем: 
или 
Второй случай: 
Итак, учитывая условие 
получаем: 
или 
Множество решений неравенства: 
Приведём другое решение.
Заметим, что исходное неравенство равносильно неравенству
Применим метод рационализации к неравенству 
:
Ответ:
Критерии проверки:
Задание 15 № 508508
Решите неравенство: 
Решение.
Преобразуем неравенство: 
Рассмотрим два случая.
а)
Откуда, учитывая условие находим: 
или 
б)
Учитывая условие 
, получаем: или
Множество решений неравенства: 
Ответ:
Критерии проверки:
Задание 15 № 508510
Решите неравенство: 
Решение.
В левой части перейдём к другому основанию:
Заметим, что при 
и 
неравенство равносильно неравенству:
Положив в последнем неравенстве 
получаем:
Таким образом, имеем:
Учитывая то, что 
получаем множество решений неравенства: 
Ответ:
Примечание.
Поясним переход от логарифма по основанию 
к десятичному логарифму. Заметим, что при 
можно произвести следующие преобразования:
Критерии проверки:
Задание 15 № 508512
Решите неравенство: 
Решение.
Заметим, что при 
и 
исходное неравенство равносильно неравенству:
Положив в последнем неравенстве 
получаем:
Далее имеем:
Учитывая то, что 
получаем решение исходного неравенства: 
Ответ:
Критерии проверки:
Задание 15 № 508513
Решите неравенство: 
Решение.
Преобразуем неравенство, используя свойства логарифма:
Рассмотрим два случая. Первый случай: 
Второй случай: 
Решение неравенства: 
или 
Приведём другое решение.
Заметим, что
Воспользуемся методом рационализации:
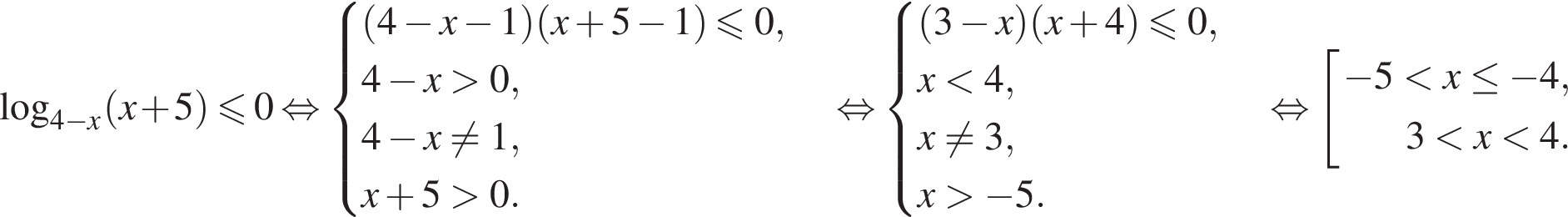
Ответ: 
Критерии проверки:
Задание 15 № 508515
Решите неравенство: 
Решение.
Рассмотрим два случая. Первый случай 
Второй случай: 
Решение первого неравенства исходной системы: 
или 
Приведём другое решение.
Используя метод рационализации, получим
Из первого неравенства
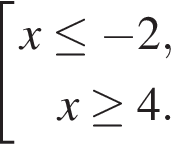
Учитывая область определения, получим
Ответ: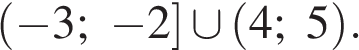 
Критерии проверки:
Задание 15 № 508517
Решите неравенство: 
Решение.
Рассмотрим два случая.
Первый случай: 
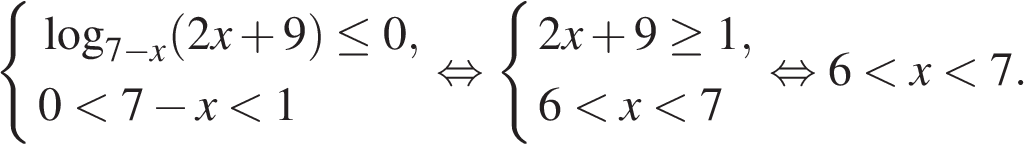
Второй случай: 
Множество решений неравенства: 
Ответ:
Критерии проверки:
Задание 15 № 508520
Решите неравенство: 
Решение.
Решим неравенство методом интервалов. Найдём ОДЗ:
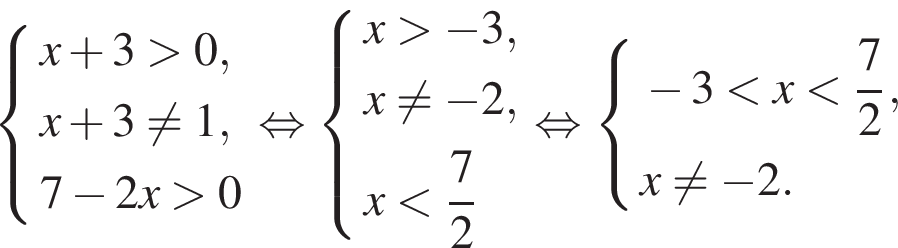
Найдём корни:
Определим знаки левой неравенства на ОДЗ (см. рис.):
Тем самым, множество решений неравенства: 
Критерии проверки:
Задание 15 № 508521
Решите неравенство: 
Решение.
Рассмотрим два случая.
Первый случай: 
Тогда имеем систему:
Второй случай: 
Тогда имеем систему:
Приведём другое решение.
Найдем сначала область определения неравенства:
На области определения исходное неравенство равносильно неравенству
Учитывая область определения, получим ответ.
Ответ: 
Критерии проверки:
Задание 15 № 508523
Решите неравенство: 
Решение.
Рассмотрим два случая.
Первый случай: 
Тогда имеем систему
Второй случай: 
Тогда имеем систему:
Множество решений неравенства: 
Ответ:
Критерии проверки:
Задание 15 № 508526
Решите неравенство: 
Решение.
Преобразуем неравенство:
Рассмотрим два случая.
Первый случай: 
откуда находим: 
Полученные значения переменной удовлетворяют условию 
Второй случай: 
Имеем:
Учитывая условие 
, получаем: 
Решение неравенства: 
Ответ:
Критерии проверки:
Задание 15 № 508527
Решите неравенство: 
Решение.
Преобразуем неравенство:
Рассмотрим два случая.
Первый случай: 
Все полученные значения переменной удовлетворяют условию
Второй случай: 
Учитывая условие 
получаем: 
Множество решений второго неравенства исходной системы: 
Ответ:
Критерии проверки:
Задание 15 № 508529
Решите неравенство: 
Решение.
Решим первое неравенство системы:
Рассмотрим два случая. Первый случай:
Второй случай:
Множество решений неравенства: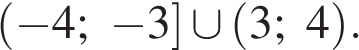 
Ответ: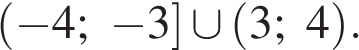
Критерии проверки:
Задание 15 № 508531
Решите неравенство: 
Решение.
Преобразуем неравенство:
Рассмотрим два случая. Первый случай:
Второй случай:
Множество решений неравенства:
Ответ:
Критерии проверки:
Задание 15 № 508533
Решите неравенство: 
Решение.
Имеем:
Рассмотрим два случая. Первый случай:
Второй случай:
Таким образом, множество решений данного уравнения: 