Заметим, что

Воспользуемся методом рационализации:

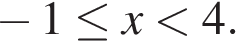
Ответ: 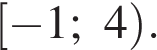
Критерии проверки:
Задание 15 № 508535
Решите неравенство: 
Решение.
Преобразуем неравенство:

Рассмотрим два случая.
а) 
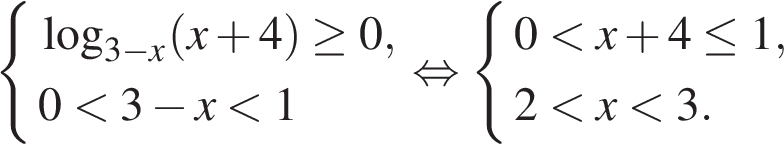
Эта система решений не имеет.
б) 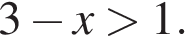

Ответ: 
Критерии проверки:
Задание 15 № 508539
Решите неравенство: 
Решение.
Последовательно получаем:

Ответ: 
Критерии проверки:
Задание 15 № 508541
Решите неравенство: 
Решение.
Решим первое неравенство системы:

Ответ: 
Критерии проверки:
Задание 15 № 508544
Решите неравенство: 
Решение.
Преобразуем неравенство, используя свойства логарифма:


Ответ: 
Критерии проверки:
Задание 15 № 508546
Решите неравенство: 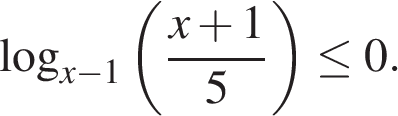
Решение.
Решим неравенство, используя теорему о знаке логарифма:

Ответ: 
Критерии проверки:
Задание 15 № 508547
Решите неравенство: 
Решение.
Значения  при которых определено первое неравенство:
при которых определено первое неравенство: 
 Рассмотрим два случая.
Рассмотрим два случая.
Первый случай:  Получаем, что
Получаем, что  Тогда
Тогда

Второй случай:  Получаем, что
Получаем, что  следовательно, при
следовательно, при 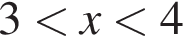 первое неравенство исходной системы верно.
первое неравенство исходной системы верно.
Таким образом, решение неравенства: 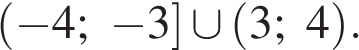
Ответ: 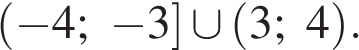
Критерии проверки:
Задание 15 № 508550
Решите неравенство: 
Решение.
Значения  при которых определено первое неравенство:
при которых определено первое неравенство:  и
и  Рассмотрим два случая.
Рассмотрим два случая.
Первый случай:  Получаем, что
Получаем, что 
 Тогда
Тогда

Второй случай:  Получаем, что
Получаем, что 
 следовательно, при
следовательно, при  первое неравенство исходной системы верно.
первое неравенство исходной системы верно.
Таким образом, решение неравенства: 
Ответ: 
Критерии проверки:
Задание 15 № 508551
Решите неравенство: 
Решение.
Значения  при которых определено неравенство:
при которых определено неравенство:  и
и  Рассмотрим два случая.
Рассмотрим два случая.
Первый случай:  Получаем, что
Получаем, что  Тогда:
Тогда:

Второй случай:  Получаем, что
Получаем, что  следовательно, при
следовательно, при  неравенство верно.
неравенство верно.
Ответ: 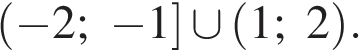
Критерии проверки:
Задание 15 № 508553
Решите неравенство: 
Решение.
Воспользуемся свойствами логарифма:

Сделаем замену 
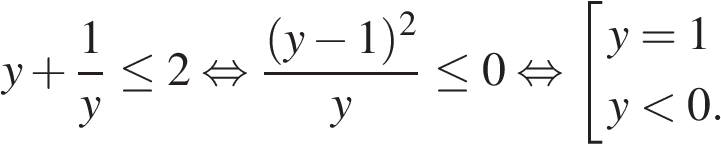
Если 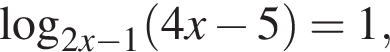 то
то

Если  то
то
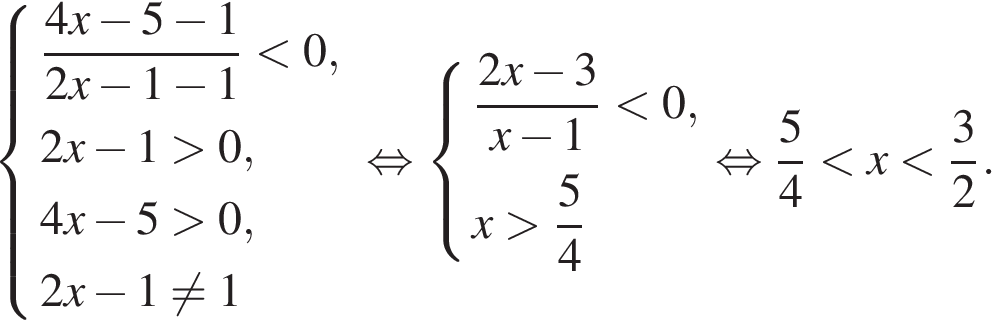
Значит, решение данного неравенства  или
или 
Ответ: 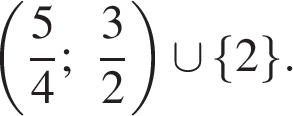
Критерии проверки:
Задание 15 № 508558
Решите неравенство: 
Решение.
Последовательно получаем:

Сделаем замену 

Тогда  или
или  откуда
откуда  или
или 
Ответ: 
Критерии проверки:
Задание 15 № 508560
Решите неравенство: 
Решение.
Рассмотрим два случая.
Первый случай: 


Откуда, учитывая условие  получаем:
получаем:  или
или 
Второй случай: 


Учитывая условие  получаем:
получаем: 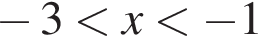 или
или 
Множество решений неравенства: 
Ответ: 
Критерии проверки:
Задание 15 № 508565
Решите неравенство: 
Решение.
Воспользуемся свойствами логарифма:

Сделаем замену 

Вернёмся к исходной переменной.
Первый случай:

Второй случай:

Итак, решение неравенства:  или
или 
Ответ: 
Критерии проверки:
Задание 15 № 508570
Решите неравенство: 
Решение.
Заметим, что выражение, стоящее под знаком логарифма, не меньше 1:

При положительных значениях переменной справедливы неравенства:  и
и  а значит,
а значит,
 и
и 
Тем самым, неравенство выполнено в том и только в том случае, когда оба выражения равны нулю.
Следовательно,

Ответ: 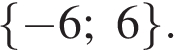
Критерии проверки:
Задание 15 № 508572
Решите неравенство: 
Решение.
Решим неравенство:

Сделаем замену 

Тогда  или
или  откуда находим решение неравенства:
откуда находим решение неравенства:  или
или 
Ответ: 
Критерии проверки:
Задание 15 № 508574
Решите неравенство: 
Решение.
Рассмотрим два случая.
Первый случай: 
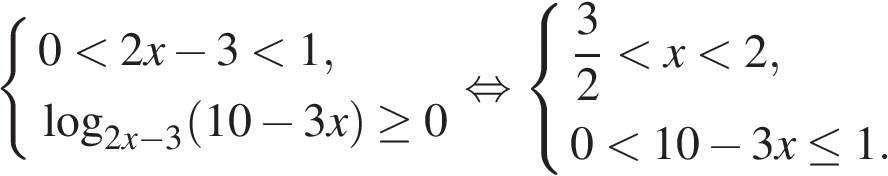
В первом случае решений нет.
Второй случай: 

Решение неравенства: 
Ответ: 
Критерии проверки:
Задание 15 № 508576
Решите неравенство: 
Решение.
Преобразуем неравенство:


Пусть  тогда неравенство примет вид:
тогда неравенство примет вид:

Рассмотрим два случая. Первый случай: 

Второй случай: 

Решение неравенства: 
Ответ: 
Критерии проверки:
Задание 15 № 508578
Решите неравенство: 
Решение.
Преобразуем неравенство:


Ответ: 
Критерии проверки:
Задание 15 № 508579
Решите неравенство 
Решение.
Неравенство имеет смысл при  и
и  Первое неравнство верно при
Первое неравнство верно при  При этих значениях переменной числитель дроби во втором неравенстве положителен, значит, положителен и знаменатель. Следовательно,
При этих значениях переменной числитель дроби во втором неравенстве положителен, значит, положителен и знаменатель. Следовательно, 
Заметим, что 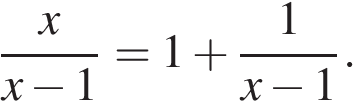 При
При  эта сумма больше 1. Тогда и основание, и аргумент выражения
эта сумма больше 1. Тогда и основание, и аргумент выражения  больше 1, а значит, левая часть исходного неравенства положительна. Тогда положительна и правая часть, откуда
больше 1, а значит, левая часть исходного неравенства положительна. Тогда положительна и правая часть, откуда 
При  обе части неравенства положительны, а аргументы логарифмов равны и больше 1. Значит, основание логарифма, стоящего в левой части неравенства, не меньше основания логарифма, стоящего в правой. На луче
обе части неравенства положительны, а аргументы логарифмов равны и больше 1. Значит, основание логарифма, стоящего в левой части неравенства, не меньше основания логарифма, стоящего в правой. На луче  имеем:
имеем:

Тем самым, 
Ответ: 
Примечание.
В решении использованы известные свойства логарифмов: если  то:
то:  и
и 
Критерии проверки:
Источник: СтатГрад: Диагностическая работа по математике 05.03.2015 вариант МА10309.
Задание 15 № 509065
Решите неравенство 
Решение.
Данное неравенство равносильно неравенству

Пусть 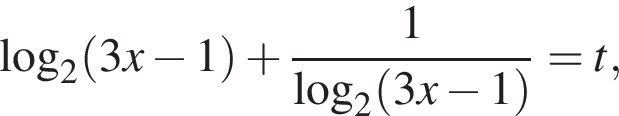 тогда
тогда 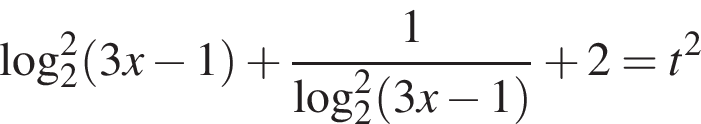 и, следовательно,
и, следовательно,

Далее имеем:  откуда
откуда
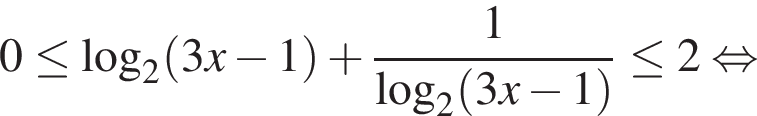
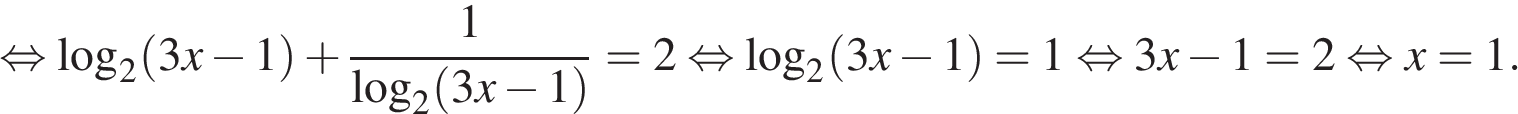
Ответ: {1}.
Критерии проверки:
Источник: Пробный экзамен по математике Санкт-Петербург 2015. Вариант 2.
Задание 15 № 509581
Решите неравенство 
Решение.
Преобразуем неравенство:
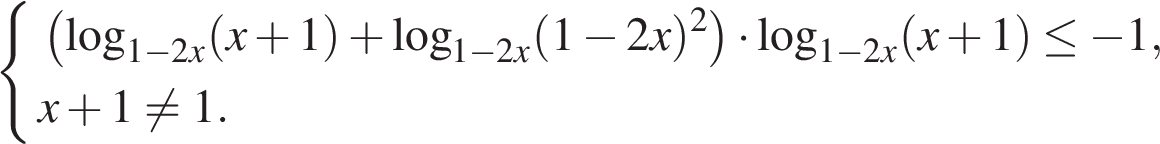
Сделаем замену  Получаем:
Получаем: 
Сделаем обратную замену:  Тогда
Тогда

откуда x = −0,5.
Ответ: −0,5.
Критерии проверки:
Источник: СтатГрад: Тренировочная работа по математике 22.04.2015 вариант МА10409.
Задание 15 № 509928
Решите неравенство 
Решение.
Преобразуем неравенство:

Сделаем замену  Получаем:
Получаем: 
Сделаем обратную замену:  Тогда
Тогда

откуда 
Ответ: 
Критерии проверки:
Источник: СтатГрад: Тренировочная работа по математике 22.04.2015 вариант МА10410.
Задание 15 № 511218
Решите неравенство 
Решение.
Ограничения на x: x > 0; x ≠ 1.
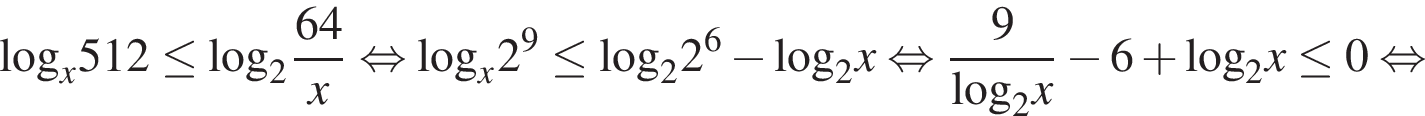

Ответ: 
Критерии проверки:
Источник: А. Ларин: Тренировочный вариант № 122.
Задание 15 № 511232
Решите неравенство 
Решение.
Найдем ограничения на x.

В логарифмах перейдем к основанию 3. Будем иметь:  Пусть
Пусть  тогда:
тогда:

Последнее неравенство решим методом интервалов.
Источник: А. Ларин: Тренировочный вариант № 124.
Задание 15 № 511246
Решите неравенство 
Решение.
Найдем ограничения на x.

Далее заданное неравенство будем рассматривать только на множестве M = (−∞; 1)∪(1; 2)∪(2; 3)∪(3; 4)∪(5;+∞).
На M:



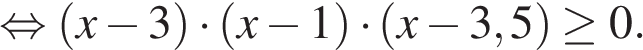
Последнее неравенство решим методом интервалов.
С учетом ограничений на х получим множество решений исходного неравенства: (1; 2)∪(2; 3)∪[ 3,5; 4)∪(5; +∞).
Ответ: 
Критерии проверки:
Источник: А. Ларин: Тренировочный вариант № 126.
Задание 15 № 511253
Решите неравенство 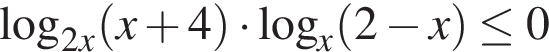
Решение.
Найдем ограничения на x.

Далее неравенство будем решать методом рационализации и будем его рассматривать только на множестве 

На M: x + 3 > 0, (x − 1)2 > 0. Следовательно,



Окончательно: 

Ответ: 
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
| Обоснованно получен верный ответ. | |
| Обоснованно получены верные ответы в обоих неравенствах исходной системы. | |
| Обоснованно получен верный ответ в одном неравенстве исходной системы. ИЛИ получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения системы неравенств. | |
| Решение не соответствует ни одному из критериев, перечисленных выше. | |
| Максимальный балл |
Источник: А. Ларин: Тренировочный вариант № 127.
Задание 15 № 511267
Решите неравенство 
Решение.
Найдем ограничения на x:

Заданное неравенство мы будем рассматривать только на множестве

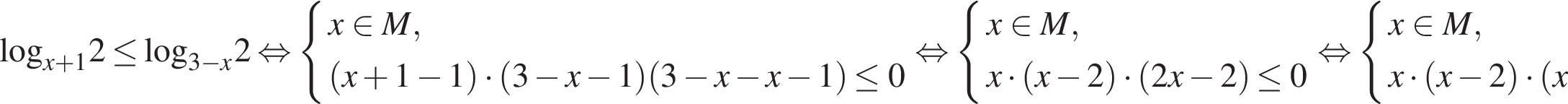
Далее решение поведем на M методом интервалов.
| Интервалы | 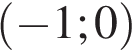
| 
| 
| 
|
| Знак выражения | − | + | − | + |
Ответ: 
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
| Обоснованно получен верный ответ. | |
| Обоснованно получены верные ответы в обоих неравенствах исходной системы. | |
| Обоснованно получен верный ответ в одном неравенстве исходной системы. ИЛИ получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения системы неравенств. | |
| Решение не соответствует ни одному из критериев, перечисленных выше. | |
| Максимальный балл |
Источник: А. Ларин: Тренировочный вариант № 129.
Задание 15 № 512483
Решите неравенство 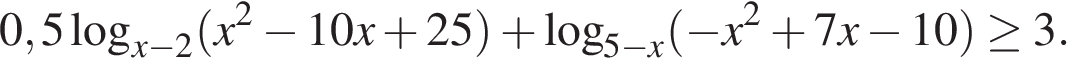
Решение.
Запишем неравенство в виде

Любое решение неравенства удовлетворяет системе
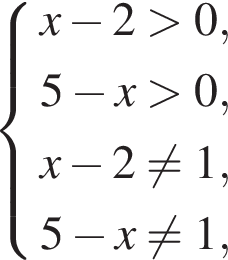
откуда

Для таких x имеем неравенство

Замена:  Получаем
Получаем  откуда z > 0. Обратная замена:
откуда z > 0. Обратная замена:

Ответ: (3; 4).
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
| Обоснованно получены верные ответы в обоих пунктах. | |
| Обоснованно получен верный ответ в пункте а или пункте б, ИЛИ получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения уравнения и отбора корней | |
| Решение не соответствует ни одному из критериев, перечисленных выше. |
Задание 15 № 512485
Решите неравенство 
Решение.
Запишем неравенство в виде
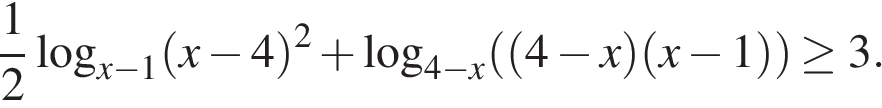
Любое решение неравенства удовлетворяет системе

откуда

Для таких x имеем неравенство

Замена:  Получаем
Получаем  откуда z > 0. Обратная замена:
откуда z > 0. Обратная замена:

Ответ: (2; 3).
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
| Обоснованно получены верные ответы в обоих пунктах. | |
| Обоснованно получен верный ответ в пункте а или пункте б, ИЛИ получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения уравнения и отбора корней | |
| Решение не соответствует ни одному из критериев, перечисленных выше. |
Задание 15 № 513257
Решите неравенство 
Решение.
Заменим  получим
получим  Определим область допустимых значений:
Определим область допустимых значений:
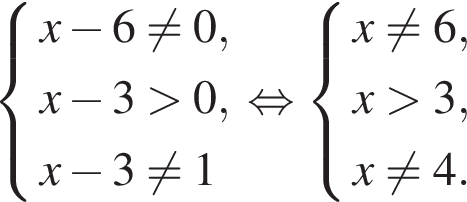
Решаем с помощью метода декомпозиции, то есть представляем логарифм в виде

получим неравенство:

Расставим точки на числовой прямой и определим знаки данного выражения на каждом из промежутков:

Учитывая область допустимых значений, получим ответ: 
Ответ: 
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
| Обоснованно получен верный ответ. | |
| Обоснованно получен ответ, отличающийся от верного только ошибками в строгости неравенства: < вместо ≤, или наоборот. Если в ответ включено значение переменной, при котором одна из частей неравенства не имеет смысла, то следует выставлять оценку «0 баллов». ИЛИ получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения. | |
| Решение не соответствует ни одному из критериев, перечисленных выше. | |
| Максимальный былл: |
Источник: Типовые тестовые задания по математике, под редакцией И. В. Ященко. 2016 г.
Задание 15 № 513274
Решите неравенство 
Решение.
Определим область допустимых значений:

Таким образом x ∈ (−2; 1) ∪ (1; 2).
Воспользуемся функцией перехода логарифма к другому основанию, получим:

И учитывая правило декомпозиции  где множитель
где множитель  можно сразу отбросить, получим
можно сразу отбросить, получим

откуда следует, что


Ответ: x ∈ (−2; −1] ∪ (1; 2).
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
| Обоснованно получен верный ответ. | |
| Обоснованно получен ответ, отличающийся от верного только ошибками в строгости неравенства: < вместо ≤, или наоборот. Если в ответ включено значение переменной, при котором одна из частей неравенства не имеет смысла, то следует выставлять оценку «0 баллов». ИЛИ получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения. | |
| Решение не соответствует ни одному из критериев, перечисленных выше. | |
| Максимальный былл: |
Источник: Типовые тестовые задания по математике, под редакцией И. В. Ященко. 2016 г.
Задание 15 № 484578
Решите неравенство 
Решение.
Перейдем к основанию 3 и упростим левую часть неравенства:
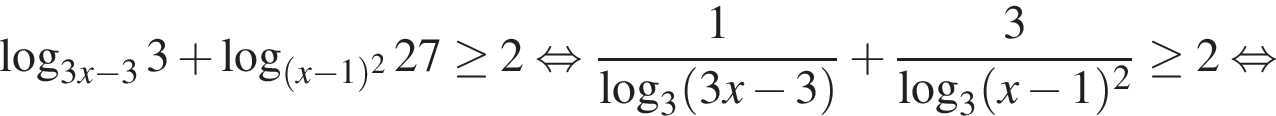

Обозначим  тогда
тогда  Решим неравенство методом интервалов:
Решим неравенство методом интервалов:

Тогда

Ответ: 
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
| Обоснованно получен верный ответ. | |
| Допущена единичная ошибка, возможно, приведшая к неверному ответу, но при этом имеется верная последовательность всех шагов решения. | |
| Решение не соответствует ни одному из критериев, перечисленных выше. |
Задание 15 № 484582
Решите неравенство 
Решение.
Чтобы был определен логарифм по основанию  это выражение должно быть положительно и отлично от 1. Находим:
это выражение должно быть положительно и отлично от 1. Находим:  откуда
откуда 
 Упростим неравенство:
Упростим неравенство: 
Заметим, что  причем равенство достигается только при
причем равенство достигается только при 
При  получаем:
получаем: 
Выделим полный квадрат в основании логарифма:  Это выражение больше 1 при всех допустимых
Это выражение больше 1 при всех допустимых 
Таким образом, 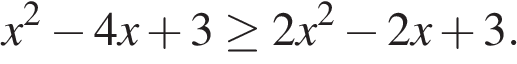
Тогда  откуда
откуда  Учитывая, что
Учитывая, что  и
и  получаем
получаем 
Ответ: 
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
| Обоснованно получен верный ответ. | |
| Допущена единичная ошибка, возможно, приведшая к неверному ответу, но при этом имеется верная последовательность всех шагов решения. | |
| Решение не соответствует ни одному из критериев, перечисленных выше. |
Задание 15 № 484581
Решите неравенство 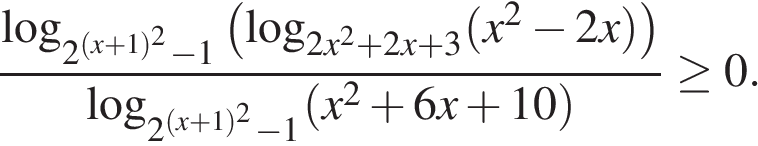
Решение.
Заметим, что
1.  и обращается в ноль только при
и обращается в ноль только при 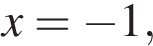 то есть и
то есть и  при
при 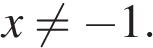
2. 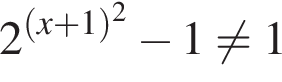 при
при  и
и 
3. 
4.  и
и 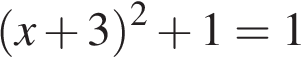 при
при  то есть
то есть  при
при 
Следовательно, при  имеем:
имеем:



Откуда с учетом выколотых точек, получаем  или
или 
Ответ: 
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
| Обоснованно получен верный ответ. | |
| Допущена единичная ошибка, возможно, приведшая к неверному ответу, но при этом имеется верная последовательность всех шагов решения. | |
| Решение не соответствует ни одному из критериев, перечисленных выше. |
Задание 15 № 485947
Решите неравенство 
Решение.
Решение ищем на множестве: 
Пусть  тогда
тогда

Значит,  или
или 
С учетом рассмотренных выше ограничений получаем множество решений исходного неравенства: 
Ответ: 
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
| Обоснованно получен верный ответ. | |
| Допущена единичная ошибка, возможно, приведшая к неверному ответу, но при этом имеется верная последовательность всех шагов решения. | |
| Решение не соответствует ни одному из критериев, перечисленных выше. |
Задание 15 № 484583
Решите неравенство 
Решение.
Запишем неравенство в виде:

Сделаем замену  и приведем левую часть к общему знаменателю:
и приведем левую часть к общему знаменателю:

Решением полученного неравенства является множество  Возвращаясь к переменной
Возвращаясь к переменной  , находим множество решений исходного неравенства:
, находим множество решений исходного неравенства: 
Ответ: 
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
| Обоснованно получен верный ответ. | |
| Допущена единичная ошибка, возможно, приведшая к неверному ответу, но при этом имеется верная последовательность всех шагов решения. | |
| Решение не соответствует ни одному из критериев, перечисленных выше. |
Задание 15 № 513685
Решите неравенство 
Решение.
Область определения неравенства задается условиями  откуда получаем
откуда получаем  На этом множестве
На этом множестве  и данное неравенство равносильно неравенству
и данное неравенство равносильно неравенству

которое, в свою очередь, равносильно неравенству

Положив  где
где  получаем неравенство
получаем неравенство  Заметим, что при
Заметим, что при  функция
функция  возрастает (произведение двух положительных возрастающих функций) и
возрастает (произведение двух положительных возрастающих функций) и  Таким образом, множество решений этого неравенства является луч
Таким образом, множество решений этого неравенства является луч 
Далее имеем:

Ответ: 
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы | ||
| Обоснованно получен верный ответ. | |||
Обоснованно получен отв<
Поиск по сайту©2015-2026 poisk-ru.ru
Все права принадлежать их авторам. Данный сайт не претендует на авторства, а предоставляет бесплатное использование. Дата создания страницы: 2019-11-29 Нарушение авторских прав и Нарушение персональных данных |
Поиск по сайту: Читайте также: Деталирование сборочного чертежа Когда производственнику особенно важно наличие гибких производственных мощностей? Собственные движения и пространственные скорости звезд |