Рассмотрим линию с двусторонним питанием (рис. 4.13), которая получается в результате преобразования простой замкнутой сети.

Рис. 4.13. Схема исходной сети
Мощности  ,
,  ,
, 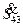 определим сначала без учета потерь по выражениям (4.4), (4.5) и (4.2).
определим сначала без учета потерь по выражениям (4.4), (4.5) и (4.2).
 ;
;
 .
.
Предположим, что направления мощностей соответствуют точке потокораздела в узле 3, который отмечен зачернённым треугольником. “Разрежем” линию в узле 3 (рис. 4.14) и рассчитаем потоки мощности в линиях 13 и 43¢, как это делалось для разомкнутой сети.
От процедуры “разрезания”, если принять, что
 ,
,  ,
,  , то, очевидно, потоки мощности в линии не изменяются.
, то, очевидно, потоки мощности в линии не изменяются.

Рис. 4.14. Представление исходной сети в виде двух линий
На участке 23 потери активной мощности
 ,
,
потери реактивной мощности  ,
,
потери полной мощности  .
.
Важно отметить, что перед определением потерь мощности справедливо допущение, что 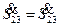 , т.е. используется результат расчета сети без учета потерь мощности.
, т.е. используется результат расчета сети без учета потерь мощности.
Находим значение потока мощности 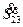 в начале участка 23 (рис. 4.15).
в начале участка 23 (рис. 4.15).

Рис. 4.15. Условные обозначения для расчета потоков в линии
с учётом потерь мощности
Далее расчет потоков мощности на участке 12 проводится как для разомкнутых сетей.
Может оказаться, что первый этап расчета кольцевой сети выявит две точки потокораздела: одну для активной, другую – для реактивной мощности. Такой случай иллюстрируется на рис. 4.16, где узел 2 – точка потокораздела для активной, а узел 3 – для реактивной мощностей.
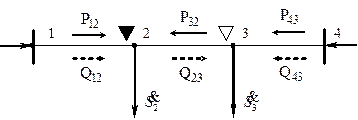
Рис. 4.16. Направления потоков в случае несовпадения точек потокораздела
активной и реактивной мощностей
В этом случае кольцевая сеть для дальнейшего расчета может быть также разделена на две разомкнутые линии. Вычислим предварительно потери мощности на участке между точками потокораздела:
 ,
,
 .
.
Если теперь принять, что в точке 2 включена нагрузка

а в точке 3 - нагрузка
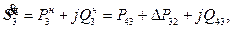
где Р12, Q12, P43, Q43 определяются по (4.4), (4.5), а P32, Q23 – по (4.2), то при дальнейшем расчёте можно вместо кольцевой схемы рассматривать две разомкнутые линии, показанные на рис. 4.17.
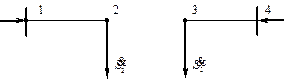
Рис. 4.17. Разделение сети при несовпадающих точках потокоразделов
Пример 4.2. Определить мощность, поступающую с шин электростанции в сеть, рассмотренную в примере 4.1. Расчет проведем с учетом потерь мощности.
Мощности  ,
,  ,
, 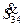 (рис. 4.13) определены без учета потерь в примере 4.1. “Разрежем” линию с двусторонним питанием в узле 3 потокораздела, как на рис. 4.18,б.
(рис. 4.13) определены без учета потерь в примере 4.1. “Разрежем” линию с двусторонним питанием в узле 3 потокораздела, как на рис. 4.18,б.
Нагрузки в узлах 3 и 3¢ равны  МВ× А =
МВ× А =  ,
, 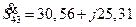 МВ× А =
МВ× А = 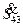 . Рассчитаем потоки мощности в линиях 23, 12 (4.18).
. Рассчитаем потоки мощности в линиях 23, 12 (4.18).
Мощность в конце линии 23 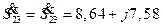 МВАр. Потери мощности в линии 23
МВАр. Потери мощности в линии 23
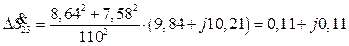 МВ×А.
МВ×А.
Мощность в конце линии 12

 МВ×А.
МВ×А.
Потери мощности в линии 12
 МВ×А.
МВ×А.
Мощность в начале линии 12
 МВ×А.
МВ×А.
Рассчитаем потоки мощности в линии 43 (4.15). Мощность в конце линии 43 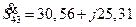 МВ×А. Потери мощности в линии 43
МВ×А. Потери мощности в линии 43
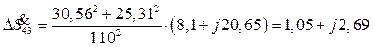 МВ×А.
МВ×А.
Мощность в начале линии 43
 МВ×А.
МВ×А.
Мощность, потребляемая с шин электростанции,
 МВ×А.
МВ×А.
Распределение напряжений в линии с двусторонним питанием. Рассмотрим схему линии с двусторонним питанием от источника 1 и 4 на рис. 4.18,а.
Линия питает две нагрузки – 2 и 3. Раздел мощностей предположим в узле 3.
Разрежем линию в узле 3 (рис. 4.18,б). Теперь можно определить напряжения или  в двух разомкнутых сетях, т.е. в линиях 13 и 43¢. Если напряжение начала линии равно напряжению конца линии (U1 = U4), то
в двух разомкнутых сетях, т.е. в линиях 13 и 43¢. Если напряжение начала линии равно напряжению конца линии (U1 = U4), то 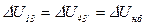 . Если U1 > U4, то
. Если U1 > U4, то  и
и  .
.
Рассмотрим послеаварийные режимы линии. Наиболее тяжелые из них – вывод из строя и отключение участков 12 или 34. Проанализируем каждый из режимов и определим наибольшую потерю напряжения  . В послеаварийном режиме, когда отключен участок 43 (рис. 4.18,в), обозначим наибольшую потерю напряжения
. В послеаварийном режиме, когда отключен участок 43 (рис. 4.18,в), обозначим наибольшую потерю напряжения  . В послеаварийном режиме, когда отключен участок 12 (рис. 4.18,г), обозначим наибольшую потерю напряжения
. В послеаварийном режиме, когда отключен участок 12 (рис. 4.18,г), обозначим наибольшую потерю напряжения  . Надо сравнить
. Надо сравнить  и
и  и определить наибольшую потерю напряжения
и определить наибольшую потерю напряжения 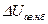 . Если линия с двухсторонним питанием имеет ответвления (рис. 4.18,д), то определение наибольшей потери напряжения усложняется. Так, в нормальном режиме надо определить потери напряжения ΔU13, ΔU43, ΔU15, сравнить их и определить
. Если линия с двухсторонним питанием имеет ответвления (рис. 4.18,д), то определение наибольшей потери напряжения усложняется. Так, в нормальном режиме надо определить потери напряжения ΔU13, ΔU43, ΔU15, сравнить их и определить  . Чтобы определить в послеаварийном режиме
. Чтобы определить в послеаварийном режиме 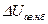 , надо рассмотреть аварийные отключения головных участков 12 и 43.
, надо рассмотреть аварийные отключения головных участков 12 и 43.

Рис. 4.18. Расчет напряжений в линии с двусторонним питанием: а) распределение потоков мощности; б) разрезание линии в точке потокораздела; в) отключение линии 43;
г) отключение линии 12; д) линия с ответвлением.
Пример 4.3. Определим напряжения в узлах 2, 3, а также  для сети рис. 4.6, рассмотренной в примерах 4.1 и 4.2, используя потоки мощностей, определенные ранее без учета потерь мощности и при их учете.
для сети рис. 4.6, рассмотренной в примерах 4.1 и 4.2, используя потоки мощностей, определенные ранее без учета потерь мощности и при их учете.
Расчет напряжений и  без учета потерь мощности, т.е. по потокам мощности, найденным в примере 4.1, проведем также и без учета поперечной составляющей падения напряжения. При U1 = U4 = 117,7 к В потери напряжения и напряжения таковы:
без учета потерь мощности, т.е. по потокам мощности, найденным в примере 4.1, проведем также и без учета поперечной составляющей падения напряжения. При U1 = U4 = 117,7 к В потери напряжения и напряжения таковы:
 кВ;
кВ;
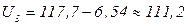 кВ;
кВ;
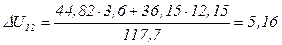 кВ;
кВ;
 кВ;
кВ;
 кВ.
кВ.
Наибольшая потеря напряжения в номинальном режиме, определяемая без учета потерь мощности,
 кВ.
кВ.
Определим напряжения и  с учетом потерь мощности, т.е. по потокам мощности, найденным в примере 4.2
с учетом потерь мощности, т.е. по потокам мощности, найденным в примере 4.2
 кВ;
кВ;
 кВ;
кВ;
 кВ;
кВ;
 кВ;
кВ;
 кВ;
кВ;
 кВ;
кВ;
 кВ.
кВ.
Таким образом, 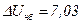 кВ.
кВ.
Погрешность расчета наибольшей потери напряжения равна
 кВ.
кВ.
Рассмотрим послеаварийные режимы (рис. 4.18,в и г).
При отключении линии 43 мощность в линии 12 (рис. 4.18,в)
 МВ×А.
МВ×А.
Мощность в линии 23
 МВ×А.
МВ×А.
Определим потери напряжения в линиях 12, 23, напряжения в узлах 2, 3, и  :
:
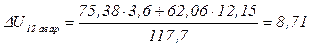 кВ;
кВ;
 кВ;
кВ;
 кВ;
кВ;
 кВ;
кВ;
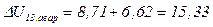 кВ.
кВ.
При отключении линии 12
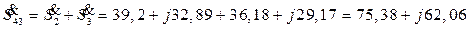 МВ×А;
МВ×А;
 МВ×А;
МВ×А;
 кВ;
кВ;
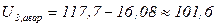 кВ;
кВ;
 кВ;
кВ;
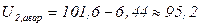 кВ;
кВ;
 кВ.
кВ.
Наибольшая потеря напряжения в послеаварийном режиме имеет место при отключении линии12, т.е.  кВ, что составляет
кВ, что составляет  %.
%.