При операциях с облигациями источником дохода являются фиксированные проценты (в случае купонных облигаций), а также разность между ценой, по которой облигация приобретается, и ценой, по которой она выкупается. Выкупная цена облигации обычно совпадает с её номиналом.
Существуют облигации без выплаты процентов (дисконтные облигации), инвестирование средств в которые будет доходным только при покупке их со скидкой с номинала, т. е. с дисконтом.
Введём обозначения:
N – номинальная стоимость облигации;
Ро – цена покупки облигации;
I0 – доход по облигации;
n – период, за который начисляются проценты;
i – процентная ставка;
ic – эффективная ставка сложных процентов.
При расчётах дохода используют понятие курса облигации Рk
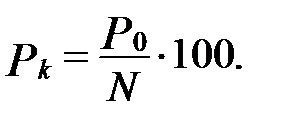
Тогда
Подставляя в эту формулу выражение Pk, получим
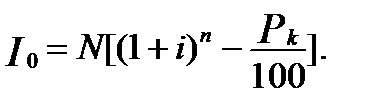
Если для измерения доходности использовать эффективную ставку сложных процентов, следует применять формулу 
:
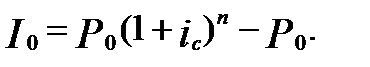
Отсюда путём несложных преобразований имеем
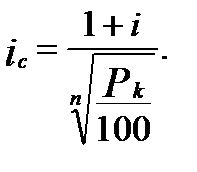
Пример 7.5
Облигация номиналом 10 000 руб., выпущенная на пять лет, приобретена по курсу 120. Рассчитать доход по облигации, если на неё ежегодно начисляются сложные проценты по ставке 18%.
Решение
Расчёт производится по формуле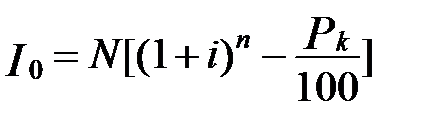 
:
I0 = 10 000 [(1 + 0,18)5 – 1,2] = 10 877,6 (руб.).
Ответ: доход по облигации составит 10 877 руб.
Пример 7.6
В условиях примера 7.5 рассчитать доходность покупки облигации в виде эффективной ставки сложных процентов.
Решение
Используем формулу :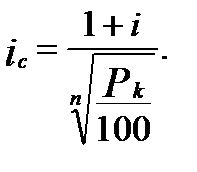
i =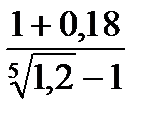 
= 0,136 = 13,6%.
Ответ: доходность покупки облигации в виде эффективной ставки сложных процентов составит 13,6%.
Доходность операций с акциями
При покупке акций источником дохода могут быть дивиденды и разница между ценой приобретения и ценой продажи.
|
|
Фиксированные дивиденды (определённый процент от номинальной стоимости акции) выплачиваются по привилегированным акциям.
Введём обозначения:
Ра – цена приобретения акции;
Q – цена продажи акции;
N – номинальная цена акции;
F – величина дивидендов;
IF – доход от дивидендов;
Ia – общий доход от покупки акции;
п – срок в годах от момента покупки до момента продажи.
Тогда Ia = IF + Q –Pa . (7.5)
Если дивиденды вновь не реинвестируются, доход от них будет равен
IF=n∙F∙N. (7.6)
Величина дивидендов по обыкновенным акциям устанавливается Общим собранием акционеров в зависимости от финансовых результатов года (дивиденды могут и не выплачиваться, если прибыли нет или она целиком направляется на развитие), поэтому расчёт дохода от таких акций может быть только ориентировочным, и производится по выражениям (7.5) и (7.6).
Выведем формулу для расчёта доходности покупки акции в виде эффективной ставки сложных процентов.
Применяем опять формулу , где S = Pa +Ia
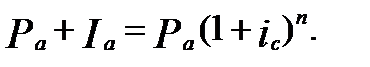
Отсюда получаем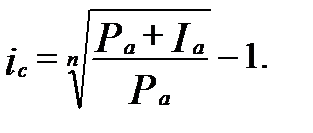 
Пример 7.7
При выпуске акций номиналом в 5 000 руб. объявленная величина дивидендов равна 15% годовых, а их стоимость, по оценкам, будет ежегодно возрастать на 4% по отношению к номиналу. Определить ожидаемый доход от покупки по номиналу и последующей продажи через пять лет 100 таких акций.
Решение
Величина годовых дивидендов от 100 акций равняется
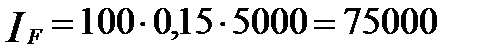(руб.).
Стоимость 100 акций через пять лет:
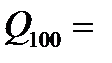100 (5 000 + 5 ∙ 0,04 ∙ 5 000) = 600 000 (руб.).
Общий доход, составит
I а = 75 000 + 600 000 – 500 000 = 175 000 (руб.).
Ответ: ожидаемый доход от покупки по номиналу и последующей продажи через пять лет 100 акций составит 175 000 руб.
|
|
Пример 7.8
В условиях примера 7.7 рассчитать доходность покупки акций в виде эффективной ставки сложных процентов.
Решение. Используем формулу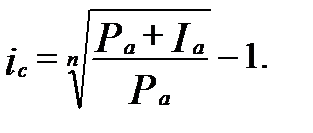
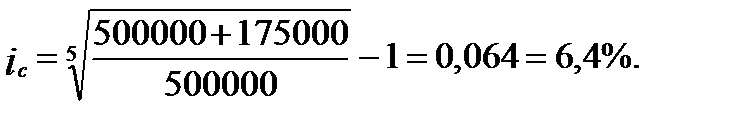
Ответ: доходность покупки акций в виде эффективной ставки сложных процентов составит 6,4%.
Вопросы для самопроверки
1. Сформулируйте цель финансовых вложений.
2. На какие виды делятся ценные бумаги в зависимости от формы
предоставления капитала и способа выплаты дохода?
3. Назовите виды долговых ценных бумаг.
4. Какие ценные бумаги называются долевыми?
5. В чём суть операции дисконтирования?
6. В каких случаях применяется антисипативный способ начисления
процентов?
7. С чем совпадает выкупная цена облигации?
8. Что является источником дохода при операциях с облигациями?
9. Что означает понятие курс облигации?
10. Что является источником дохода при покупке акций?