МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ
ФГАОУ ВО "Севастопольский государственный университет"
Кафедра «Менеджмент организаций»
Методические указания
к лабораторной работе №2
«Использование многофакторного регрессионного анализа
В маркетинговых исследованиях»
по дисциплине “Методы маркетинговых исследований”
для студентов всех форм обучения
Севастополь
УДК 658.
Методические указания по выполнению лабораторной работы №2 «Использование многофакторного регрессионного анализа в маркетинговых исследованиях» по дисциплине "Методы маркетинговых исследований" / Сост. И.А. Гребешкова. ¾ Севастополь: Изд-во СевНТУ, 2016. ¾ 12 с.
Целью методических указаний является применение теоретических знаний по теме "Методы маркетинговых исследований" при решении ситуаций с помощью лицензионной системы MINITAB. Методические указания предназначены для студентов экономических специальностей.
Методические указания рассмотрены и утверждены на заседании кафедры менеджмент организаций (протокол № от " " __2016 г.)
Допущено учебно-методическим центром СевГУ в качестве методических указаний
Рецензенты:
Содержание
1 Многофакторный регрессионный анализ. 4
Мультиколлинеарность. 4
2 Многофакторный регрессионный анализ в системе MINITAB.. 5
3 Задание по выполнению лабораторной работы.. 6
Литература. 11
Многофакторный регрессионный анализ
Регрессионный анализ объединяет широкий круг задач. связанный с построением функциональных зависимостей между двумя группами числовых переменных: 
и 
. Для краткости объединим в многомерную переменную 
. 
— в переменную 
, и будем говорить об исследовании зависимости между и . При этом будем считать независимой переменной. влияющей на значения . В связи с этим будем называть откликом. а =() – факторами, влияющими на отклик.
Многомерная линейная регрессия позволяет построить и проверить модель линейной связи между одной зависимой (эндогенной) и несколькими независимыми (экзогенными) переменными.
Уравнение множественной регрессии (то есть регрессии с двумя и более переменными) имеет вид:
,
где 
— зависимая переменная, 
— независимая переменная, 
— коэффициенты регрессионного уравнения, 
— ошибка с нормальным законом распределения, средним равным нулю и стандартным отклонением s. Матричная запись модели имеет вид:
,
где 
— вектор-столбец значений зависимой переменной,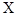 
— детерминированная матрица объясняющих переменных (регрессоров), 
— вектор столбец параметров модели, 
— вектор столбец ошибок.
Статистический подход к задаче построения функциональной зависимости от основывается на предположении, что нам известны некоторые исходные (экспериментальные) данные (
), где 
— значение отклика при заданном значении фактора 
, 
изменяется от 1 до n. Пару значений (
) часто называют результатом одного измерения, а n – числом измерений.
Мультиколлинеарность
Одним из условий регрессионного анализа является независимость объясняющих переменных. При анализе реальных, экономических процессов это условие часто нарушается. Например, в работе оценщика цена продаваемого дома может быть связана со значениями таких независимых переменных, как год постройки дома, его жилая площадь. Количество жилых комнат и прочих помещений, общее количество продаваемых домов, индекс, учитывающий качество конструкции продаваемого дома. В таких случаях жилую площадь, количество жилых комнат и прочих помещений следует рассматривать вместе. Если одно из этих значений возрастает, другие тоже, как правило, увеличиваются.
Линейная зависимость между двумя или более переменными называется мультиколлинеарностью. Степень мультиколлинеарности измеряется фактором роста дисперсии (VIF):
, j=1,2, …,k
Здесь 
— это коэффициент детерминации из регрессии j-ой независимой переменной по оставшимся (k-1) независимым переменным. Если j-я независимая переменная 
не связана с остальными 
, =0 и 
. Если зависимость имеет место, то 
.
Значение 
, близкое к 1, говорит о том, что для этой переменной проблемы мультиколлинеарности не существует. Оценка ее коэффициента и значение t–статистики не изменяется значительно, если другие независимые переменные будут добавлены в уравнение регрессии или удалены из него. Значение , гораздо большее 1, указывает, что оценка коэффициента при этой независимой переменной неустойчива. В сущности, большая величина фактора означает, что имеется избыточная информация о независимых переменных. Информация, предоставляемая переменной с большим , уже присутствует в других независимых переменных. При наличии мультиколлинеарности интерпретировать влияние отдельной независимой переменной на зависимую гораздо сложнее.
Многофакторный регрессионный анализ в системе MINITAB
Для проведения регрессионного анализа необходимо:
1) ввести данные;
2) Stat > Regression > Regression – позволяет выполнить простую или множественную регрессию (построение зависимости между откликом и переменной), и заполнить следующие ячейки:
Response – переменная отклика;
Predictors – независимые переменные;
Options – опции;
Graphs – построение графиков;
Storage – сохранение полученных результатов;
Stat > Regression > Stepwise — позволяет выполнить прямую (включение) и обратную (исключение независимых переменных) пошаговую регрессию;
Stat > Regression > Best Subsets – позволяет осуществить выбор влияющих переменных из потенциального множества переменных на основе R2 критерия.
Stat > Regression > Fitted Line Plot — позволяет построить линейную, квадратическую или кубическую регрессии от одной переменной.Пункты диалогового окна:
Response [Y] — переменная отклика или независимая переменная,
Predictor [X] — независимая переменная.
Type of Regression Model (типы моделей регрессии):
Linear — модель линейной регрессии,
Quadratic — модель квадратичной регрессии,
Cubic — модель кубической регрессии.
3) При проведении многофакторного регрессионного анализа t-критерий Стьюдента обеспечивает эффективную проверку предельного вклада каждой переменной при допущении, что все другие переменные уже включены в уравнение. Если объясняющая способность независимых переменных перекрывается (присутствует мультиколлинеарность), то предельный вклад в объяснение каждой из переменных может быть небольшим (t – статистика для переменных не значима), в то же время, как F-статистика указывает на адекватность.
4) В MINITAB для проверки явления мультиколлинеарности необходимо в команде Stat > Regression > Regression в опции Options отметить Variance inflation factors: — фактором роста дисперсии (VIF). Если значение VIF очень велико, то оно свидетельствует о том, что данная переменная связана с стальными переменными. О наличии связи между переменными может указывать выборочный коэффициент корреляции. На следующем этапе удаляется та переменная из модели, у которой значение t-статистики будет наименьшим.