Второстепенные балки монолитного ребристого перекрытия по своей статистической схеме представляет собой многопролётные неразрезные балки
Рис.2 Геометрические размеры и опоры усилий второстепенной балки.
Расчёт таких балок, выполняется так же как и для плит, учётом перераспределения в следствии пластических деформаций. Для вычисления пролётов второстепенных балок задаёмся размерами главноё балки:
высотой:
hгл.б.=(1/10….1/16)lгл.б.=(1/10….1/16)*600=60…37.5 см.
принимаем hгл=50 см
считаем ширину bгл.б=(1/2….1/3)hгл.б=(1/2….1/3)*50=25…16 см.
принимаем 
=25 см.
Расчётные пролёты второстепенных балок
L0.0=6000 - 125 - 200 +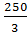 
=5760 мм
L0.1=6000-250 = 5750 мм
Расчёт нагрузки на 1 м погонный балки постоянная:
Постоянная нагрузка от плиты и пола:
q = 3.08 кН/м2
b = 2 м
qпл =3,08×2= 6,16 кН/м
от собственного веса второстепенной балки:
qвт.б.=(hвт.б. –hпл. )× bвт.б× 
× γfm = (0,45 – 0,06) ×25×0,18×1,1= 1,9305 кН/м
где:
- удельный вес железобетона 25 кН/м3
b - ширина второстепенной балки
γfm – коэффициент надёжности по нагрузки 1,1
полезная нагрузка:
pпол = р + b =4×2 =8 кН/м
полная расчётная нагрузка на 1 погонныё метр:
q = qпол +pпол = 8+8,0905 =16,095 кН/м
Вычисление расчётных усилий.
У статистических расчётов второстепенных балок с разными пролётами или такими, которые отличаются не более чем 20%, расчётные моменты определяют, используя метод гранитного равновесия.
Момент в первом пролёте:
M1= 
кН*м
Момент на опоре В:
Момент в средних пролётах и на опоре С:
M2= 
кН*м
Мс=- 33.25 кН ·м
Определение поперечных сил Q
на крайней опоре:
QА=(q×а1)= 16.0905 × 5.76x0.4=37.07 кН
на средней опоре:
QB=-(q×а2)= 16.0905 × 5.75x0.6=-55.51 кН
|
|
в остальных опорах:
QB=(q×а3)= 16.0905 × 5.75x0.5=46.26 кН
Уточнение размеров второстепенных балок.
Необходимой толщиной плиты задаёмся с экономических размышлений % армирования плиты в пределах µ=0,8-1% принимаем µ=0,8% по max пролётном моменте. Mmax=M1= 64.97кН/м при b =100 см.
Полезная высота сечения плиты при
ξ =μ*(RS/RB*γb2)=0.01*(365/14.5*0.9)=0.279
где Rb=14.5 МПа - расчётное сопротивление бетона на сжатие (для класса В-25);
Rs=365 МПа расчётное сопротивление арматуры при растяжении (для класса А 400С);
γb2 =0.9 – коэффициент условия работы бетона.
Используем таблицу коэффициентов для расчёта изгибающих элементов армированных одиночной арматурой, по величине ξ находим соответствующие ему коэффициент αm=0,241
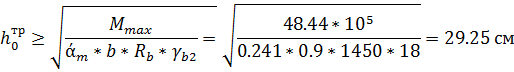
b- ширина второстепенной балки
Полная высота сечения
h= h0 +а=29.25+3=32.35 см;
принимаем h = 35см и b = 18 см
Подбор арматуры плиты перекрытия
| Сечение | М, кН*см | 
| ξ | Необходимая арматура
| Необходимая арматура | |
| Количество и тип сеток | As,, см2 | |||||
| Пр1 | 
| 0,9036 | 
| 6.16 | ||
| Оп В |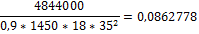 
| 0,9036 |
| 6.03 | ||
| Пр2 | 
| 0,9364 | 
| 4.52 | ||
| Оп С |
| 0,9364 |
| 3.39 |
Расчёт наклонных сечений на поперечную силу:
При максимальном диаметре продольной арматуры Ø14 из условия свариваемости принимаем для расчёта поперечную арматуру, принимаем Ø6А240С (Аsw1= 0.283см2) при 2-х каркасах (n=2) (Аsw=2 ×Аsw1=2×0.283=0.566 см2)
По конструктивным требованиям шаг поперечных стержней:
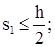
Проверяем условия по проценту армирования:
Определяем единичные усилия воспринимаемые поперечными стержнями
Rsw=175 МПа
Длина проекции наибольшего невыгодного сечения
|
|
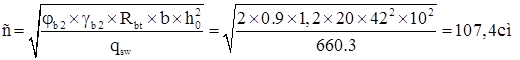
h0=h-a=30-3=27см, с≤2h0
Определяем усилие, воспринимаемое поперечными стержнями
Qsw= qsw × c=660,3×107,4=70916=70,92kH
Определяем усилие, воспринимаемое бетоном
Определяем условие прочности
Qmax< Qsw+ Qb
74,3kH<70,92+70,95=141,87 kH Поперечная арматура для второстепенной балки применяется Ø6А240С с шагом S1 =15cм на приопорных участках длиной 1/4длины пролёта, а в середине пролёта с шагом S2=30см.