Дифракция света. Дифракционная решетка.

дифракция света — отклонение света от прямолинейного рас­пространения на резких неоднородностях среды

Зоны Френеля

Принцип Гюйгенса — Френеля: волновая поверх­ность в любой момент времени представляет собой не просто огибающую вторичных волн, а результат их интерференции.

Для того чтобы найти амплитуду световой волны от точечного моно­хроматического источника света А в произвольной точке О изо­тропной среды, надо источник света окружить сферой радиусом r=ct. Интерференция волны от вторичных источников, располо­женных на этой поверхности, определяет амплитуду в рассмат­риваемой точке О, т. е. необходимо произвести сложение коге­рентных колебаний от всех вторичных источников на волновой поверхности. Так как расстояния от них до точки О различны, то колебания будут приходить в различных фазах. Наименьшее расстояние от точки О до волновой поверхности В равно r₀. Первая зона Френеля ограничивается точками волновой поверхности, рассто­яния от которых до точки О равны: 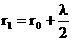, где λ — длина световой волны. Вторая зона .

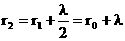Аналогично определяются границы других зон. Если разность хода от двух соседних зон равна половине длины волны, то коле­бания от них приходят в точку О в противоположных фазах и на­блюдается интерференционный минимум, если разность хода равна длине волны, то наблю­дается интерференционный максимум.

Таким образом, если на препятствии укладывается целое число длин волн, то они гасят друг друга и в данной точке наблюдается минимум (темное пятно). Если нечетное число полуволн, то наблюдается максимум (светлое пятно).

Расчеты позволили понять, каким образом свет от точечного источника, испускающего сферические волны, достигает про­извольной точки О пространства.

Дифракция от различных препятствий:

a. от тонкой прово­лочки;

b. от круглого отверстия;

c. от круглого непрозрачного экрана.

Дифракция происходит на предметах любых размеров, а не только соизмеримых с длиной волны λ. Трудности наблюдения заключаются в том, что вследствие малости длины световой волны интерференционные максиму­мы располагаются очень близко друг к другу, а их интенсив­ность быстро убывает.

Дифракция наблюдается хорошо на расстоянии .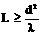

Если 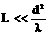, то дифракция невидна и получается резкая тень

(d - диаметр экрана). Эти соотношения определяют границы применимости геометрической оптики. Если наблюдение ведется на расстоянии ,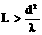

где d — размер предмета, то начинают проявляться волновые свойства света. На рис. показана примерная зависимость результатов опыта по распространению волн в зависимости от соотношения размеров препятствия и длины волны.

Дифракционная решетка - система препятствий (параллельных штрихов), сравнимых по размерам с длиной волны.

Величина d = a + b называется постоянной (периодом) дифракционной решетки, где а — ширина щели; b — ширина непрозрачной части. Угол φ - угол отклонения световых волн вследствие дифракции. Наша задача - определить, что будет наблюдаться в произвольном направлении φ - максимум или минимум. Оптическая разность хода 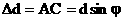Из условия максимума интерференции получим: . Следовательно: 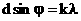- формула дифракционной решетки. Величина k — порядок дифракцион­ного максимума

(равен 0, ± 1, ± 2 и т.д.).

Принцип Гюйгенса. Каждая точка волнового фронта может рассматриваться как источник вторичных сферических волн, распространяющихся со скоростью света в данной среде; огибающая поверхность всех вторичных сферических волн (т.е. поверхность, касательная к фронтам всех вторичных волн) в любой момент времени представляет собой новое положение волнового фронта исходной волны.

Исходя из этого принципа, легко доказать, что световые лучи в однородной среде распространяются прямолинейно.

Закон отражения волн: падающий луч, луч отраженный и перпендикуляр к отражающей поверхности лежат в одной плоскости. Угол падения равен углу отражения.

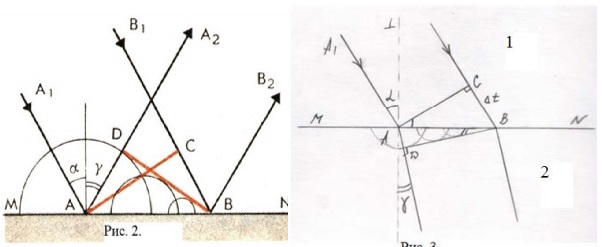Доказательство. (рис. 2). Рассмотрим два параллельных луча А1А и В1В плоской волны, падающих на поверхность MN под углом α. Луч В1В достигнет поверхности спустя время t после луча А1А. Если v – скорость волны, то ВС=vt. В момент касания поверхности луча В1В вторичные волны образуют ряд сферических поверхностей, огибающая к которым представляет собой плоскость BD, причем AD=vt. Треугольники ABD и ABC равны по 1 признаку, следовательно угол DBA равен углу CAB, а угол DBA равен углу γ,как углы с взаимно перпендикулярными сторонами, значит угол γ равен углу α (угол падения равен углу отражения. 2. Закон преломления волн: падающий луч, луч преломленный и перпендикуляр к преломляющей поверхности лежат в одной плоскости. Отношение синусов углов падения и преломления есть величина постоянная для данных двух сред.

Доказательство. (рис. 3). Преломление волн вызвано различием их скоростей в различных средах. Пусть на поверхность MNпадает плоская волна под углом α. Пусть скорости распространения волн в средах 1 и 2 равны соответственно v1 и v2. Тогда к моменту, когда луч В1В достигнет преломляющей поверхности (ВС=v1t), вторичная волна от точки А распространится на расстояние v2t. Волновая поверхность- плоскость BD. Угол γ = углу ABD, как видно из рисунка: 𝑠𝑖𝑛𝛼 𝑠𝑖𝑛𝛾 = 𝐶𝐵 𝐴𝐷 = 𝑣1𝑡 𝑣2𝑡 или 𝑠𝑖𝑛𝛼 𝑠𝑖𝑛𝛾 = 𝑣1 𝑣2 = 𝑛, где n- показатель преломления втрой