{
Тесты по математическому анализу
Разработчик – ст. преп. кафедры высшей математики-1 Заволженская В. Л.
}
ТЕСТ № 4.1.1
 существует, если функция f (x, y) в замкнутой области D:
1. не определена; 2. неограниченна; +3. непрерывна; 4. произвольная. существует, если функция f (x, y) в замкнутой области D:
1. не определена; 2. неограниченна; +3. непрерывна; 4. произвольная.
|
ТЕСТ № 4.1.2
Заштрихованная часть
 является областью интегрирования повторного интеграла
является областью интегрирования повторного интеграла 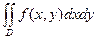 :
+1. :
+1.  ; 2. ; 2.  ; 3. ; 3. 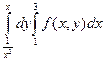 ; 4. ; 4. 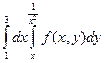 . .
|
ТЕСТ № 4.1.3
Заштрихованная часть
 является областью интегрирования повторного интеграла
является областью интегрирования повторного интеграла 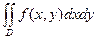 :
1. :
1. 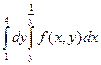 ; +2. ; +2.  ; 3. ; 3.  ; 4. ; 4.  . .
|
ТЕСТ № 4.1.4
Заштрихованная часть
 является областью интегрирования повторного интеграла
является областью интегрирования повторного интеграла 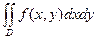 :
1. :
1.  ; +2. ; +2.  ; 3. ; 3.  ; 4. ; 4. 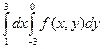 . .
|
ТЕСТ № 4.1.5
Область D ограничена линиями: y = j 1(x), y = j 2(x), x = a, x = b и j 1(x) £ j 2(x), a < b. Тогда интеграл 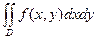 равен:
1. равен:
1.  ; +2. ; +2. 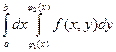 ; 3. ; 3.  ; 4. ; 4.  . .
|
ТЕСТ № 4.1.6
Область D ограничена линиями: x = j 1(y), x = j 2(y), y = c, y = d и j 1(y) £ j 2(y),
a < b. Тогда интеграл 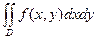 равен:
1. равен:
1.  ; 2. ; 2.  ; +3. ; +3.  ; 4. ; 4.  . .
|
ТЕСТ № 4.1.7
Двойной интеграл 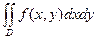 , где область D ограничена линиями y = x, y = x 2, равен:
1. , где область D ограничена линиями y = x, y = x 2, равен:
1.  ; +2. ; +2. 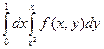 ; 3. ; 3.  ; 4. ; 4.  . .
|
ТЕСТ № 4.1.8
Двойной интеграл 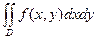 , где область D ограничена линиями y = x 2, , где область D ограничена линиями y = x 2, 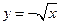 , x = 1, равен:
+1. , x = 1, равен:
+1. 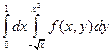 ; 2. ; 2.  ; 3. ; 3.  ; 4. ; 4.  . .
|
ТЕСТ № 4.1.9
Двойной интеграл 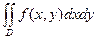 , где область D ограничена линиями y = x, y = 2 x,
x = 1, x = 2, равен:
1. , где область D ограничена линиями y = x, y = 2 x,
x = 1, x = 2, равен:
1.  ; +2. ; +2. 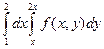 ; 3. ; 3. 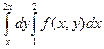 ; 4. ; 4.  . .
|
ТЕСТ № 4.1.10
Изменив порядок интегрирования в интеграле 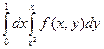 , получим:
1. , получим:
1.  ; 2. ; 2.  ; 3. ; 3.  ; +4. ; +4.  . .
|
ТЕСТ № 4.1.11
Изменив порядок интегрирования в интеграле  , получим:
1. , получим:
1.  ; 2. ; 2.  ; +3. ; +3. 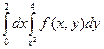 ; 4. ; 4.  . .
|
| ТЕСТ № 4.1.12 Площадь области, ограниченной кривыми линиями y = 2 x – x 2 и y = x 2, равна S. Тогда 6 S равны: Эталон ответа: 2. |
| ТЕСТ № 4.1.13 Объём V тела, ограниченного поверхностями z = 6 – 3 x – 2 y, z = 0, x = 0, y = 0 равен: Эталон ответа: 6. |
ТЕСТ № 4.1.14
Объём тела, ограниченного поверхностями
z = 4 - x 2 - y2, z = 0, x = 0, y = 0 равен V. Тогда  равно:
Эталон ответа: 2. равно:
Эталон ответа: 2.
|
ТЕСТ № 4.1.15
Объём тела, ограниченного поверхностями z = 1 - x 2 - y2, z = 0 равен V. Тогда  равно:
Эталон ответа: 2. равно:
Эталон ответа: 2.
|
ТЕСТ № 4.2.1
Пусть V – область интегрирования: 0 £ x £ 1, 0 £ y £ 3, 0 £ z £ 4. Тогда  равен:
1. 6. +2. 12. 3. 3. 4. 4. равен:
1. 6. +2. 12. 3. 3. 4. 4.
|
ТЕСТ № 4.2.2
Объём тела, ограниченного поверхностями  , z = 2, z = 4 равен V. Тогда , z = 2, z = 4 равен V. Тогда  равно:
+1. 8. 2. 32. 3. 16. 4. 4. равно:
+1. 8. 2. 32. 3. 16. 4. 4.
|
ТЕСТ № 4.2.3
Объём тела, ограниченного поверхностями  , z = 3, z = 5 равен V. Тогда , z = 3, z = 5 равен V. Тогда  равно:
+1. 18. 2. 36. 3. 16. 4. 4. равно:
+1. 18. 2. 36. 3. 16. 4. 4.
|
ТЕСТ № 4.2.4
Объём тела, ограниченного поверхностями z = 8 - x 2 - y2, z = 4 равен V. Тогда  равно:
Эталон ответа: 8. равно:
Эталон ответа: 8.
|
ТЕСТ № 4.2.5
Объём тела, ограниченного поверхностями z = 9 - x 2 - y2, z = 5 равен V. Тогда 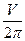 равно:
Эталон ответа: 4. равно:
Эталон ответа: 4.
|
ТЕСТ № 4.2.6
Объём тела, ограниченного поверхностями z = 5 - x 2 - y2, z = 3 + x 2 + y 2 равен V. Тогда  равно:
Эталон ответа: 1. равно:
Эталон ответа: 1.
|
ТЕСТ № 4.2.7
Объём тела, ограниченного поверхностями z = 3 - x 2 - y2, z = 1 + x 2 + y 2 равен V. Тогда  равно:
Эталон ответа: 3. равно:
Эталон ответа: 3.
|
| ТЕСТ № 4.2.8 Масса тела, ограниченного поверхностями x = 0, x = 1, y = 0, y = 3, z = 0, z = 4, и r = x – его плотность в любой точке тела. Тогда масса тела равна: 1. 3; +2. 6; 3. 12; 4. 4. |
| ТЕСТ № 4.2.9 Масса тела, ограниченного поверхностями x = 0, x = 1, y = 0, y = 2, z = 0, z = 4, и r = y – его плотность в любой точке тела. Тогда масса тела равна: 1. 3; 2. 6; 3. 12; +4. 8. |
ТЕСТ № 4.2.10
Масса тела, ограниченного поверхностями  , x = 0, y = 0, z = 2, z = 4, и r = x – его плотность в любой точке тела. Тогда масса тела равна:
1. 3; 2. 6; +3. , x = 0, y = 0, z = 2, z = 4, и r = x – его плотность в любой точке тела. Тогда масса тела равна:
1. 3; 2. 6; +3.  ; 4. ; 4.  . .
|
ТЕСТ № 4.3.1
Криволинейный интеграл  по длине дуги АВ, заданной уравнением, по длине дуги АВ, заданной уравнением, 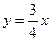 , точки А (0; 0), В (- 4; - 3) равен:
1. 27; 2. 42; +3. 40; 4. 13,5. , точки А (0; 0), В (- 4; - 3) равен:
1. 27; 2. 42; +3. 40; 4. 13,5.
|
ТЕСТ № 4.3.2
Криволинейный интеграл  по длине дуги АВ, заданной уравнением, по длине дуги АВ, заданной уравнением,  , точки А (0; 0), В (3; 4) равен:
1. 27; 2. 32; 3. 54; +4. 37,5. , точки А (0; 0), В (3; 4) равен:
1. 27; 2. 32; 3. 54; +4. 37,5.
|
ТЕСТ № 4.3.3
Масса проволоки в форме полуокружности  переменной плотности r = xy в каждой точке проволоки равна:
+1. 4. 2. 8. 3. 12. 4. 24. переменной плотности r = xy в каждой точке проволоки равна:
+1. 4. 2. 8. 3. 12. 4. 24.
|
ТЕСТ № 4.3.4
Масса проволоки в форме полуокружности  переменной плотности r = xy в каждой точке проволоки равна:
1. 4. 2. 13,5. 3. 12. 4. 24. переменной плотности r = xy в каждой точке проволоки равна:
1. 4. 2. 13,5. 3. 12. 4. 24.
|
ТЕСТ № 4.3.5
Криволинейный интеграл второго рода  вдоль кривой у = х 2 от точки А (1, 1) до точки В (- 1, 1) равен:
1. 2; +2. - 2; 3. 4; 4. - 4. вдоль кривой у = х 2 от точки А (1, 1) до точки В (- 1, 1) равен:
1. 2; +2. - 2; 3. 4; 4. - 4.
|
ТЕСТ № 4.3.6
Криволинейный интеграл второго рода  вдоль кривой у = х 2 от точки А (- 1, 1) до точки В (1, 1) равен:
1. 2; +2. 2; 3. 4; 4. - 4. вдоль кривой у = х 2 от точки А (- 1, 1) до точки В (1, 1) равен:
1. 2; +2. 2; 3. 4; 4. - 4.
|
ТЕСТ № 4.3.7
Криволинейный интеграл  равен:
+1. 2; 2; -2; 3. 1; 4. -1. равен:
+1. 2; 2; -2; 3. 1; 4. -1.
|
ТЕСТ № 4.3.8
Полный дифференциал функции U (x, y) имеет вид: dU = ydx + xdy. Тогда функция U (x, y) равна:
+1. U = xy + C; 2. U = x + y + C; 3. U = x - y + C; 4. 
|
ТЕСТ № 4.3.9
Работа силы  , точка приложения которой x = t 2, y = t, 0 £ t £ 1, равна:
1. , точка приложения которой x = t 2, y = t, 0 £ t £ 1, равна:
1.  ; 2. ; 2.  ; +3. 1; 4. - 1. ; +3. 1; 4. - 1.
|
ТЕСТ № 4.3.10
Работа силы  , точка приложения которой x = t 3, y = t, 0 £ t £ 1, равна:
1. , точка приложения которой x = t 3, y = t, 0 £ t £ 1, равна:
1. 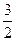 ; 2. ; 2.  ; 3. - 1; +4. 1. ; 3. - 1; +4. 1.
|
!END