Дифференцирование параметрически заданных функций

39.

Определение.

Производной функции в точке называется предел отношения приращения функции в этой точке к приращению аргумента , при (если этот предел существует и конечен), т.е.

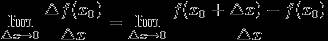
Смысл производной - это скорость изменения ф-ции при изменении аргумента.

Геометрический смысл производной.

Производная в точке x₀ равна угловому коэффициенту касательной к графику функции y=f(x) в этой точке.

Физического смысла производной

Давайте вспомним что такое скорость и ускорение? Скорость - это расстояние делить на время, т.е. скорость - это расстояние, пройденное за единицу времени, значит скорость - первая производная от расстояния. Ускорение - это скорость делить на время, т.е. ускорение - это скорость в единицу времени, значит ускорение - первая производная от скорости. В этом заключается физический смысл производной.

Теоремы.

Пусть функция определена на некотором множестве , и . Назовём точку точкой максимума функции на множестве , если при всех выполняется неравенство , и точкой минимума, если при всех выполняется неравенство .

Точка 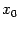, являющаяся либо точкой максимума, либо точкой минимума, называется точкой экстремума.

Если y(x)=f(u(x)) и существует f’(u) и u’(x), то существует y’(x)=f(u(x))u’(x).

Ферма. Пусть функция имеет на множестве точку экстремума , причём множество содержит некоторую -окрестность 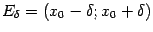точки 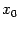. Тогда либо имеет в точке 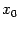производную, равную 0, то есть , либо производная в точке 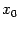не существует.

Ролль. Пусть функция дифференцируема на интервале , непрерывна в точках и и принимает в этих точках значение 0: . Тогда найдётся хотя бы одна точка , в которой .

Лагранж. Пусть функция дифференцируема на интервале и непрерывна в точках и . Тогда найдётся такая точка , что

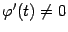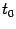Коши. Пусть функции и дифференцируемы на интервале и непрерывны при и , причём при всех . Тогда в интервале найдётся такая точка , что

Определение.

Итак, график дифференцируемой функции в окрестности каждой своей точки сколь угодно близко приближается к графику касательной в силу равенства: где α – бесконечно малая в окрестности 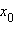функция. Для приближенного вычисления значения функции f в точке x₀ + Δx эту бесконечно малую функцию можно отбросить:

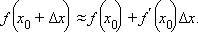
Линейную функцию называют дифференциалом функции f в точке 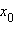и обозначают df. Для функции x производная в каждой точке 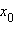равна 1, то есть Поэтому пишут:

Дифференциалом функции называется величина, пропорциональная б.м. приращению аргумента Dх и отличающаяся от соответствующего приращения функции на б.м.в. более высокого порядка малости, чем Dх.

Геометрический смысл: дифференциал - изменение ординаты касательной, проведенной к графику функции в точке (x₀,f(x₀)) при изменении x₀ на величину Dx.

Свойства:

1. (U±V)`=U`±V`, то (U±V)`dx=U`dx±V`dx, d(U±V)=d(U±V)

2. (UV)`=U`V+V`U, то (UV)`dx=V`dU+U`dV

3.d(c)=c`dx=0*dx=0

4. d(U/V)`=(V`dU-U`dV)/V².

Инвариантность формы первого дифференциала

Если x - независимая переменная, то dx = x - x ₀ (фиксированное приращение). В этом случае имеем

df (x ₀) = f' (x ₀) dx.

Если x = φ (t) - дифференцируемая функция, то dx = φ' (t ₀) dt. Следовательно,

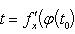
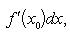
т. е. первый дифференциал обладает свойством инвариантности относительно замены аргумента.

Инвариантность - неизменность чего-либо при определённых преобразованиях переменных

Дифференцирование параметрически заданных функций

Пусть функция задана параметрическими уравнениями

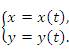
где t – параметр.
Тогда производная этой функции по переменной x равна отношению производных и 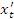по параметру t: