▼ Математическим ожиданием, или средним значением, непрерывной случайной величины X называется постоянная, которую обозначают символом  иопределяют равенством
иопределяют равенством 
Замечание. Как и в случае дискретного распределения, математическое ожидание для дискретных случайных величин можно интерпретировать как центр масс. Действительно, если предположить, что вдоль вещественной прямой непрерывно распределена масса с плотностью распределения 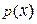 , то выражение для математического ожидания можно интерпретировать как центр масс. Поэтому точно так же, как и в случае дискретного распределения, математическое ожидание можно рассматривать как центральную точку случайной величины.
, то выражение для математического ожидания можно интерпретировать как центр масс. Поэтому точно так же, как и в случае дискретного распределения, математическое ожидание можно рассматривать как центральную точку случайной величины.
Для непрерывных случайных величин математическое ожидание обладает теми же свойствами, что и для дискретных случайных величин. Перечислим их:
1. Математическое ожидание постоянной равно ей самой 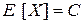 .
.
2. Постоянный множитель можно выносить за знак математического ожидания 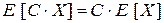 .
.
3. Математическое ожидание алгебраической суммы конечного числа случайных величин равно такой же сумме их математических ожиданий, т. е.  .
.
4. Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий, т. е.  . Данное свойство естественным образом распространяется на любое число независимых случайных величин.
. Данное свойство естественным образом распространяется на любое число независимых случайных величин.
Для вычисления числовых характеристик непрерывной случайной величины удобно использовать формулу 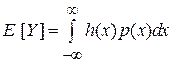 , в которой
, в которой  некоторая функция, случайная величина
некоторая функция, случайная величина  определяется равенством
определяется равенством  , а p (x)
, а p (x)  плотность распределения случайной величины X. Отметим, что приведенная формула для математического ожидания
плотность распределения случайной величины X. Отметим, что приведенная формула для математического ожидания  не является определением этого математического ожидания, а доказывается с использованием соотношений между плотностями случайных величин X и Y.
не является определением этого математического ожидания, а доказывается с использованием соотношений между плотностями случайных величин X и Y.
Дисперсией непрерывнойслучайной величины X называется математическое ожидание квадрата ее отклонения от математического ожидания, т. е.

Отметим, что в этой формуле использовано приведенное выражение для математического ожидания случайной величины  при
при 
Дисперсия случайной величины характеризует рассеяние (вариацию, разброс) этой величины относительно ее математического ожидания. Дисперсия  имеет размерность квадрата случайной величины, что не всегда удобно. Поэтому в качестве показателя рассеяния используют также величину
имеет размерность квадрата случайной величины, что не всегда удобно. Поэтому в качестве показателя рассеяния используют также величину  , называемую среднеквадратическим отклонением случайной величины X.
, называемую среднеквадратическим отклонением случайной величины X.
Свойства дисперсии:
1. Дисперсия константы равна нулю. Это свойство вытекает из соотношений 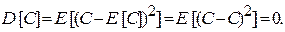
2. Постоянный множитель можно выносить за знак дисперсии, возведя его при этом в квадрат, т. е. 
3. Дисперсия суммы конечного числа независимых случайных величин равна сумме их дисперсий, т. е.  .
.
4. Дисперсия случайной величины равна разности между математическим ожиданием квадрата случайной величины и квадратом ее математического ожидания  . Это соотношение становится очевидным, если раскрыть квадрат под знаком математического ожидания в формуле, определяющей дисперсию. ▲
. Это соотношение становится очевидным, если раскрыть квадрат под знаком математического ожидания в формуле, определяющей дисперсию. ▲
Задача 3.1. X и Y независимые случайные величины, имеющие стандартное равномерное распределение. Найти математическое ожидание и дисперсию случайной величины Z = ma x (X, Y).
Решение. В задаче 2.3 была получена плотность распределения случайной величины Z. Эта плотность равна

Поэтому



Задача 3.2. График плотности распределения случайной величины X представляет собой треугольник с вершинами в точках ( 1, 0), (0, 1) и (1, 0).
1, 0), (0, 1) и (1, 0).
Написать выражение для плотности распределения и функции распределения, найти E [ X ], D [ X ].
Решение. Плотность распределения случайной величины X имеет вид

Потому, учитывая то, что функция p (x) является четной, получим
 Поскольку математическое ожидание равно нулю,
Поскольку математическое ожидание равно нулю,  = 1/6.
= 1/6.
Задача 3.3. Пусть X – случайная величина имеющая нормальное распределение с параметрами  т. е. с плотностью распределения
т. е. с плотностью распределения
φ  Найти E [ X ] и D [ X ].
Найти E [ X ] и D [ X ].
Решение. В соответствии с определением вычислим математическое ожидание:


Здесь использовано то, что 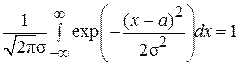 как интеграл от плотности нормального распределения, a
как интеграл от плотности нормального распределения, a  как интеграл от нечетной функции по симметричному множеству. Таким образом, показано, что E [ X ] = a.
как интеграл от нечетной функции по симметричному множеству. Таким образом, показано, что E [ X ] = a.
Перейдем к вычислению дисперсии.

После замены переменных  и интегрирования по частям получим
и интегрирования по частям получим
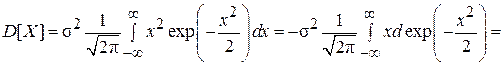

Таким образом, 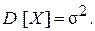
Задача 3.4. X и Y независимы и имеют стандартное нормальное распределение. Определим случайные величины U = max(X, Y), V = min(X, Y). Определить E (U  V).
V).
Решение. Пусть  функция распределения и плотность распределения стандартного нормального закона. Тогда
функция распределения и плотность распределения стандартного нормального закона. Тогда
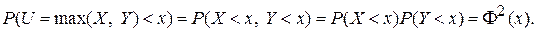
Поэтому плотность распределения q (x) случайной величины U равна
 Таким образом, получим
Таким образом, получим

Интегрируя по частям, получим

Заметим, что нормальная случайная величина с математическим ожиданием, равным нулю, и дисперсией, равной  , имеет плотность распределения
, имеет плотность распределения  Интеграл от этой плотности распределения равен единице. Поэтому
Интеграл от этой плотности распределения равен единице. Поэтому  Из соображений симметрии ясно, что
Из соображений симметрии ясно, что 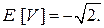 Таким образом,
Таким образом, 
Задача 3.5. Пусть случайные величины X и Y независимы и имеют стандартное нормальное распределение. Определить 
Решение. Случайная величина Z = 2 X + 3 Y, будучи линейной комбинацией независимых нормальных величин, также имеет нормальное распределение с математическим ожиданием, равным 2 + 3 = 5, и с дисперсией, равной 4 + 9 = 13. Поэтому плотность распределения случайной величины Z и математическое ожидание случайной величины  равны, соответственно,
равны, соответственно,  и
и 


Здесь использован тот факт, что, будучи интегралом от плотности нормального распределения, интеграл 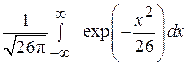 равен единице.
равен единице.
▼ Ковариацией двух случайных величин X и Y называется число 
 Его следует рассматривать как меру линейной зависимости случайных величин X и Y. Иногда его также рассматривают как меру стохастической зависимости X и Y, но это правомерно только в том случае, когда X и Y имеют совместное нормальное распределение. Изучение таких распределений выходит за пределы данных методических указаний.
Его следует рассматривать как меру линейной зависимости случайных величин X и Y. Иногда его также рассматривают как меру стохастической зависимости X и Y, но это правомерно только в том случае, когда X и Y имеют совместное нормальное распределение. Изучение таких распределений выходит за пределы данных методических указаний.
Перечислим свойства ковариации. Здесь a, b – вещественные числа.
1. Симметричность, т. е. 
2. Линейность, т. е. 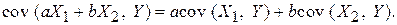 Это свойство естественным образом переносится на любое число слагаемых.
Это свойство естественным образом переносится на любое число слагаемых.
3. Инвариантность относительно сдвига, т. е. 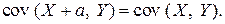
С помощью ковариации можно вычислять дисперсию суммы зависимых случайных величин по формуле 
Коэффициентом корреляции двух случайных величин X и Y называется число 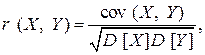 т. е. коэффициент корреляции – это нормированная ковариация. Перечислим его свойства:
т. е. коэффициент корреляции – это нормированная ковариация. Перечислим его свойства:
1. Симметричность, т. е. 
2. Изменения при линейных преобразованиях:
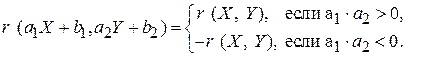
Таким образом, коэффициент корреляции сохраняется, если оба линейных преобразования возрастают или убывают одновременно. ▲
Задача 3.6. Случайный вектор ( X, Y ) равномерно распределен в круге  Найти E X, D X, E Y, D Y, cov(X, Y) и коэффициент корреляции.
Найти E X, D X, E Y, D Y, cov(X, Y) и коэффициент корреляции.
Решение. Введем случайные величины  Тогда совместная плотность распределения случайных величин
Тогда совместная плотность распределения случайных величин  равна
равна  если
если 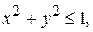 и равна 0
и равна 0  в противном случае. Поскольку эта плотность является четной функцией своих аргументов, то справедливы равенства
в противном случае. Поскольку эта плотность является четной функцией своих аргументов, то справедливы равенства  Поэтому
Поэтому  Остается вычислить дисперсии:
Остается вычислить дисперсии:

Задача 3.7. Известно, что D (X) = 1, D (Y) = 4, коэффициент корреляции равен 0.5. Найти коэффициент корреляции между 2 X + Y + 1 и X + 2 Y.
Решение. В соответствии с определениями ковариации и коэффициента корреляции


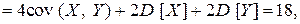



Поэтому искомый коэффициент корреляции 