В настоящем разделе приведенынеобходимые сведения для решения задач. Более подробно они описаны в [1] применительно к дискретным распределениям.
▼ Предполагается, что имеется некоторое непрерывное множество объектов произвольной природы, называемое множеством элементарных событий или пространством элементарных событий.
Событие в теории вероятностей – это множество, состоящее из элементарных событий.
Достоверным событием называется событие, состоящее из всех элементарных событий. Достоверное событие происходит всегда, поскольку в результате случайного выбора какое-то элементарное событие всегда реализуется. Обозначим достоверное событие буквой  .
.
Невозможным событием называется событие, которое не может произойти никогда. Обозначим его  . Оно представляет собой пустое множество элементарных событий.
. Оно представляет собой пустое множество элементарных событий.
Противоположным событию  называется событие
называется событие  , состоящее в том, что событие
, состоящее в том, что событие 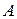 не произошло.
не произошло.  состоит из элементарных событий, не входящих в А. Противоположным для достоверного события является невозможное событие.
состоит из элементарных событий, не входящих в А. Противоположным для достоверного события является невозможное событие.
Суммой (объединением) событий А и В называетсясобытие  , состоящее в том, что из двух событий
, состоящее в том, что из двух событий 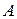 и
и  происходит, по крайней мере, одно (либо
происходит, по крайней мере, одно (либо 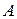 , либо
, либо  , либо
, либо 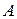 и
и  вместе). Событию
вместе). Событию  соответствует множество элементарных событий А
соответствует множество элементарных событий А  В. Поэтому иногда мы будем использовать знак объединения вместо знака суммирования.
В. Поэтому иногда мы будем использовать знак объединения вместо знака суммирования.
Произведением (пересечением) событий А и В называется событие  , состоящее в том, что события
, состоящее в том, что события 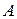 и
и  происходят одновременно.Событию
происходят одновременно.Событию  соответствует множество элементарных событий
соответствует множество элементарных событий  . Поэтомуиногда мы будем использовать знак пересечения вместо знака произведения.
. Поэтомуиногда мы будем использовать знак пересечения вместо знака произведения.
Суммой n событий называется событие, состоящее в том, что произошло хотя бы одно из исходных событий.
Произведением n событий называется событие, состоящее в том, что одновременно произошли все исходные события.
Приведенные определения соответствуют операциям объединения и пересечения соответствующих множеств элементарных событий.
Разностью событий А и В называется событие  которое состоит в том, что происходит событие
которое состоит в том, что происходит событие 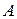 и не происходит
и не происходит  . В разность входят элементарные события из A, не входящие в B (
. В разность входят элементарные события из A, не входящие в B ( ).
).
В отличие от дискретного случая, для непрерывного множества элементарных событий  не все его подмножества являются событиями. Совокупность всех событий образует множество подмножеств из
не все его подмножества являются событиями. Совокупность всех событий образует множество подмножеств из  , обладающих следующими свойствами:
, обладающих следующими свойствами:
1) достоверное событие  является событием;
является событием;
2) невозможное событие является событием;
3) сумма и произведение любого числа событий являются событиями;
4) отрицание любого события является событием.
Для каждого события 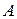 определена его вероятность
определена его вероятность  , обладающая свойствами:
, обладающая свойствами:
1) 
2) если последовательность событий  … попарно несовместна, то
… попарно несовместна, то 
3) вероятность невозможного события равна нулю;
4) для любого события 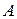 справедливо равенство
справедливо равенство 
5) справедливо равенство, называемое теоремой сложения вероятностей 
События A и B называются независимыми, если P (AB) = P (A) P (B).
Три события A, B и C называются независимыми в совокупности, если выполняются следующие четыре соотношения: 



Несколько событий называются независимыми в совокупности, если подобные соотношения выполняются для любого подмножества рассматриваемых событий. ▲
Задача 1.1. На координатной плоскости находится единичный квадрат:  Из него случайным образом выбирается точка
Из него случайным образом выбирается точка  с координатами
с координатами  . Событие
. Событие  состоит в том, что
состоит в том, что  . Найти вероятность события
. Найти вероятность события  .
.
Решение. Полноемножество элементарных событий  состоит из точек указанного в условии задачи единичного квадрата. Введем события:
состоит из точек указанного в условии задачи единичного квадрата. Введем события: 
 Тогда
Тогда  так как эти события геометрически представляют собой прямоугольники со сторонами, равными 1 и
так как эти события геометрически представляют собой прямоугольники со сторонами, равными 1 и  а вероятностью событий являются площади соответствующих множеств. Событие
а вероятностью событий являются площади соответствующих множеств. Событие  состоит из точек квадрата со стороной
состоит из точек квадрата со стороной  поэтому
поэтому  так что эти события независимы. Легко видеть, что
так что эти события независимы. Легко видеть, что 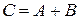 . Применяя к этим событиям приведенную теорему сложения вероятностей, получим
. Применяя к этим событиям приведенную теорему сложения вероятностей, получим  =
= 
Задача 1.2. Два не очень пунктуальных человека договорились встретиться под часами в 12 ч 30 мин. Каждый из них с равной вероятностью может прийти в любой момент времени между 12 и 13 ч. Найти вероятность того, что первый из них придет на 15 мин позже второго.
Решение. Перенесем начало координат в точку (12,12). Пусть компонентывектора  являются моментамиприхода к месту встречи встречающихся людей в этой системе координат. Тогда
являются моментамиприхода к месту встречи встречающихся людей в этой системе координат. Тогда  состоит из точек
состоит из точек  , для которых
, для которых  . Эти точки, как и в предыдущей задаче, заполняют квадрат со стороной, равной 1 ч. Пусть событие
. Эти точки, как и в предыдущей задаче, заполняют квадрат со стороной, равной 1 ч. Пусть событие  состоит в том, что первый из встречающихся придет на 1/4 ч позже второго. Тогда на координатной плоскости этому событию соответствует треугольник с вершинами в точках (1/4, 0), (1, 0), (1, 3/4). Это прямоугольный треугольник с катетами, равными по 3/4. Его площадь равна 9/32. Поэтому вероятность события
состоит в том, что первый из встречающихся придет на 1/4 ч позже второго. Тогда на координатной плоскости этому событию соответствует треугольник с вершинами в точках (1/4, 0), (1, 0), (1, 3/4). Это прямоугольный треугольник с катетами, равными по 3/4. Его площадь равна 9/32. Поэтому вероятность события  равна 9/32.
равна 9/32.
▼ В рамках теоретико-вероятностной схемы, когда предполагается, что имеется некоторое пространство  элементарных событий, случайной величиной
элементарных событий, случайной величиной 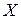 называют измеримую функцию, заданную на множестве элементарных событий
называют измеримую функцию, заданную на множестве элементарных событий  . Случайные величины обычно обозначаются большими буквами латинского алфавита X, Y, Z и т. д., причем зависимость от элементарного события
. Случайные величины обычно обозначаются большими буквами латинского алфавита X, Y, Z и т. д., причем зависимость от элементарного события  часто не указывается явно.
часто не указывается явно.
Замечание. Измеримость случайной величины  , означает, что событиями являются все подмножества множества элементарных событий
, означает, что событиями являются все подмножества множества элементарных событий  вида
вида 
 ,
,  .
.
Функция множества  называется распределением случайной величины X. Распределение случайной величины содержит в себе всю вероятностную информацию об этой случайной величине. С ее помощью можно вычислить вероятности любых событий, связанных с рассматриваемой случайной величиной.
называется распределением случайной величины X. Распределение случайной величины содержит в себе всю вероятностную информацию об этой случайной величине. С ее помощью можно вычислить вероятности любых событий, связанных с рассматриваемой случайной величиной.
Функцией распределения F (x) случайной величины Х называется функция, определяемая соотношением  . С помощью этой функции также можно вычислить распределение случайной величины. Функция распределения случайной величины представляет собой неубывающую функцию, обладающую следующими свойствами:
. С помощью этой функции также можно вычислить распределение случайной величины. Функция распределения случайной величины представляет собой неубывающую функцию, обладающую следующими свойствами:
1)  ,
,  ;
;
2)  непрерывна слева.
непрерывна слева.
Говорят, что случайная величина X имеет непрерывное (абсолютно непрерывное) распределение, если ее функция распределения  представима в виде
представима в виде  Входящая в эту формулу функция
Входящая в эту формулу функция  называется плотностью распределения случайной величины X и обладает двумя свойствами:
называется плотностью распределения случайной величины X и обладает двумя свойствами:
1)  2)
2) 
Плотность распределения случайной величины определяется функцией распределения с помощью формулы 
Случайные величины, обладающие непрерывным распределением, называют непрерывными случайными величинами.
Плотность распределения  случайной величины
случайной величины 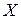 допускает дифференциальную интерпретацию:
допускает дифференциальную интерпретацию: 
Говорят, что случайная величина X имеет равномерное распределение на интервале (a, b), если ее плотность распределения имеет вид

Легко видеть, что случайно выбранная точка из интервала (a, b) имеет равномерное распределение.
При a = 0, b = 1 равномерное распределение носит название стандартного равномерного распределения. ▲
Задача 1.3. Найти функцию распределенияслучайной величины X, равномерно распределенной на интервале (a, b).
Решение. Согласно определениюплотности распределения,при 

При  плотность распределения
плотность распределения  равна нулю, поэтому функция распределения F (x) для этих значений x также равна нулю. При x > b плотность распределения
равна нулю, поэтому функция распределения F (x) для этих значений x также равна нулю. При x > b плотность распределения  равна нулю. Поэтому для таких значений x
равна нулю. Поэтому для таких значений x

Таким образом,

| (1.1) |
Задача 1.4 (п реобразование Смирнова).Непрерывная случайная величина 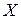 с положительной плотностью распределения
с положительной плотностью распределения  и возрастающей функцией распределения
и возрастающей функцией распределения  преобразуется в новую случайную величину
преобразуется в новую случайную величину  по формуле
по формуле  . Найти функцию распределения
. Найти функцию распределения  и плотность распределения
и плотность распределения  случайной величины
случайной величины  .
.
Решение. По определению функции распределения для любого  справедливы соотношения
справедливы соотношения 
 Здесь использован тот факт, что в условиях задачи у функции F (x) существует однозначно определенная обратная функция
Здесь использован тот факт, что в условиях задачи у функции F (x) существует однозначно определенная обратная функция  такая, что для
такая, что для  выполняется равенство
выполняется равенство  . Поскольку 0 ≤ F (y) ≤ 1, то Q (y) = 0 для y < 0 и Q (y) = 1 для y > 1.
. Поскольку 0 ≤ F (y) ≤ 1, то Q (y) = 0 для y < 0 и Q (y) = 1 для y > 1.
Приведенные выкладки показывают, что случайная величина Y имеет стандартное равномерное распределение на интервале (0,1). Поэтому

| 
|
Задача 1.5. Случайная величина X имеет равномерное распределение на интервале (a, b). Известно, что F (0) = 1/4, F (1) = 1/2. Найти параметры a и b.
Решение. Поскольку F (0) и F (1) меньше единицы, то выполняются условия (см. (1.1))

| 
|
Решив эту систему уравнений, получим a =  , b = 3.
, b = 3.
Задача 1.6. Функция распределения случайной величины X, имеет вид

Найти постоянную С и плотность распределения случайной величины X.
Решение. Использовав приведенные ранее свойства функции распределения, получим  Таким образом,
Таким образом,  Дифференцируя, получим
Дифференцируя, получим 
Замечание. Распределение случайной величины задачи 1.6называется распределением Коши.
▼ Говорят, что случайная величина X имеет показательное распределение с параметром  , если ее плотность распределения имеет вид
, если ее плотность распределения имеет вид
 ▲
▲
Задача 1.7. Случайная величина X имеет показательное распределение с параметром  . Найти q (y) плотность распределения случайной величины
. Найти q (y) плотность распределения случайной величины  .
.
Решение. Пусть Q (y) – функция распределения случайной величины Y. Тогда Q (y) =  где F(x)
где F(x)  функция распределения случайной величины X. Дифференцируя это равенство по переменной y и учитывая, что производную в правой части нужно рассматривать как производную сложной функции, получим при y >1
функция распределения случайной величины X. Дифференцируя это равенство по переменной y и учитывая, что производную в правой части нужно рассматривать как производную сложной функции, получим при y >1
 .
.
Поскольку случайная величина X положительна, то случайная величина  Поэтому при y < 1 выполняется равенство q (y) = 0.
Поэтому при y < 1 выполняется равенство q (y) = 0.
Замечание. Легко видеть, что если случайная величина Y имеет плотность распределения, то ее функция распределения непрерывна, откуда следует, что  для любой постоянной a. Из этого следует, что в задаче 1.6 можно положить в качестве значения q (1) любое число. Положим
для любой постоянной a. Из этого следует, что в задаче 1.6 можно положить в качестве значения q (1) любое число. Положим  для того, чтобы функция q (y) была непрерывной на множестве
для того, чтобы функция q (y) была непрерывной на множестве  .
.
▼ Говорят, что случайная величина X имеет нормальное распределение с параметрами  , если ее плотность распределения имеет вид
, если ее плотность распределения имеет вид
.
 . .
| (1.2) |
Если m = 0 и  то распределение случайной величины X называют стандартным нормальным распределением. Нормальное распределение является наиболее распространенным распределением в теории вероятностей. ▲
то распределение случайной величины X называют стандартным нормальным распределением. Нормальное распределение является наиболее распространенным распределением в теории вероятностей. ▲
Задача 1.8. Случайная величина X имеет нормальное распределение с параметрами m = 1 и  = 4. Определить
= 4. Определить  .
.
Решение. При b > a множества  и
и  не пересекаются, так что события
не пересекаются, так что события 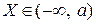 и
и  несовместны. Поэтому из свойств вероятности следует, что
несовместны. Поэтому из свойств вероятности следует, что  таким образом,
таким образом,  .
.
Пусть теперь случайная величина X имеет нормальное распределение с параметрами m и  Тогда
Тогда  где
где  − функция распределения стандартного нормального закона.
− функция распределения стандартного нормального закона.
Применительно к рассматриваемой задаче, используя таблицы стандартного нормального распределения, получим

=  .
.
Замечание. При решении этой задачи использовались два свойства функции распределения нормального закона:
1) 
| 2) 
|
Первое из этих свойств рассматривается в разд. 2. Второе свойство легко вытекает из того, что плотность стандартного нормального закона является четной функцией. Действительно,
 .
.
Задача 1.9. Является ли функцией распределения функция
 ?
?
Решение. Поскольку эта функция не является монотонно возрастающей, то она не является функцией распределения.
Задача 1.10. График плотности распределения случайной величины представляет собой треугольник с вершинами в точках ( 1, 0), (0, 1) и (1, 0). Написать выражение для плотности распределения p (x) и функции распределения (x) случайной величины X. Найти
1, 0), (0, 1) и (1, 0). Написать выражение для плотности распределения p (x) и функции распределения (x) случайной величины X. Найти  .
.
Решение. Очевидно,



Задача 1. 11. Непрерывная случайная величина X распределена по закону Коши с функцией распределения  Определить, какие значения могут принимать постоянные a, b, c. Определить соответствующую плотность распределения.
Определить, какие значения могут принимать постоянные a, b, c. Определить соответствующую плотность распределения.
Решение. Использовав общие свойства функций распределения, получим

Поэтому  Поскольку функция распределения F (x) не убывает, то a > 0. Таким образом,
Поскольку функция распределения F (x) не убывает, то a > 0. Таким образом,  где a > 0. Дифференцируя F (x), найдем плотность распределения
где a > 0. Дифференцируя F (x), найдем плотность распределения 
Задача 1.12. Маяк, расположенный в километре от прямолинейного берега моря, посылает на берег луч под углом  , равномерно распределенным в интервале
, равномерно распределенным в интервале  Найти плотность распределения координаты «зайчика» от луча на берегу. Координатой является расстояние от основания перпендикуляра, проведенного от маяка к берегу, взятого со знаком «+», если луч отклоняется от перпендикуляра вправо, и со знаком «
Найти плотность распределения координаты «зайчика» от луча на берегу. Координатой является расстояние от основания перпендикуляра, проведенного от маяка к берегу, взятого со знаком «+», если луч отклоняется от перпендикуляра вправо, и со знаком « », если – влево.
», если – влево.
Решение. Пусть A – место положения маяка, B – точка основания перпендикуляра, проведенного из точки A к берегу, C – точка положения «зайчика» на берегу.  Поэтому, поскольку угол
Поэтому, поскольку угол  равномерно распределен на интервале
равномерно распределен на интервале  то
то 

 функция распределения закона Коши. Используя решение задачи 1.11, получим
функция распределения закона Коши. Используя решение задачи 1.11, получим 
▼ Пусть X – случайная величина с плотностью распределения p (x), а случайная величина Y определяется равенством Y = h (X), где h (x) – дифференцируемая монотонная функция. Пусть q (y) – плотность распределения случайной величины Y. Как связаны между собой эти плотности распределения? На этот вопрос отвечает следующая теорема.
Теорема 1.1. Пусть 
 функция, обратная к функции h (x). Тогда
функция, обратная к функции h (x). Тогда
 ▲
▲
Задача 1.13. Пусть X – случайная величина с плотностью распределения p (x), а случайная величина Y определяется равенством Y = aX + b. Определить плотность распределения случайной величины Y.
Решение. Здесь h (x) = ax + b,  = (y – - b)/ a,
= (y – - b)/ a, 
Поэтому 
Задача 1.14. Пусть X – случайная величина с плотностью распределения φ(x) (плотность распределения стандартного нормального закона) и функцией распределения  . Пусть случайная величина Y определяется равенством Y = aX + b. Определить плотность распределения q (y) и функцию распределения Q (y) случайной величины Y.
. Пусть случайная величина Y определяется равенством Y = aX + b. Определить плотность распределения q (y) и функцию распределения Q (y) случайной величины Y.
Решение. Используя задачу 1.13 и формулу (1.2), получим

Полученная плотность распределения является плотностью распределения нормального закона с параметрами b и  Точно таким же образом можно получить, что если q (x) – плотность распределения нормального закона с параметрами b и
Точно таким же образом можно получить, что если q (x) – плотность распределения нормального закона с параметрами b и  то случайная величина Y= (X – b) /a имеет стандартное нормальное распределение. Далее,
то случайная величина Y= (X – b) /a имеет стандартное нормальное распределение. Далее,

Задача 1.15. Пусть X – случайная величина, имеющая стандартное равномерное распределение, а случайная величина Y определяется равенством Y = – a ln X + b, где a > 0.Определить плотность распределения случайной величины Y.
Решение. Имеем
h (x)= –a ln X + b,  =
= 

Поэтому, в соответствии с теоремой 1.1,

Поскольку область значений случайной величины X – это интервал (0, 1), то область значений случайной величины Y – это множество  Поэтому приведенная формула для q (y) верна на множестве
Поэтому приведенная формула для q (y) верна на множестве  в то время как на дополнительном множестве
в то время как на дополнительном множестве  эта плотность равна нулю. Отметим, что при b = 0 плотность распределения q (y) является плотностью распределения показательного закона с параметром, равным 1/ a.
эта плотность равна нулю. Отметим, что при b = 0 плотность распределения q (y) является плотностью распределения показательного закона с параметром, равным 1/ a.
Задача 1.16. Пусть X – случайная величина, имеющая стандартное нормальное распределение с плотностью распределения φ(x),  Найти плотность распределения q (y) случайной величины Y.
Найти плотность распределения q (y) случайной величины Y.
Решение. Поскольку случайная величина X принимает любые числовые значения, то функция h (x) не монотонна. Поэтому для нахождения плотности распределения случайной величины Y нельзя применять теорему 1.1. Для решения задачи сначала найдем функцию распределения Q (y) случайной величины Y. Очевидно, Q (y) = 0при y < 0. При 

Дифференцируя это равенство, получим при 

Очевидно, q (y) = 0 при y < 0.
2. СОВМЕСТНОЕ РАСПРЕДЕЛЕНИЕ
НЕСКОЛЬКИХ СЛУЧАЙНЫХ ВЕЛИЧИН
▼ Пусть имеется n случайных величин  Назовем функцией распределения вектора X = (
Назовем функцией распределения вектора X = ( ) функцию n переменных
) функцию n переменных

где 
 пробегает множество всех возможных значений случайного вектора X.
пробегает множество всех возможных значений случайного вектора X.
Как и в случае функции распределения случайной величины, функция распределения случайного вектора однозначно определяет  X
X  для любого n -мерного множества A.
для любого n -мерного множества A.
Функцию распределения случайного вектора называют также совместной функцией распределения случайных величин  . Эта функция обладает следующими свойствами:
. Эта функция обладает следующими свойствами:
1. 
2.  не убывает по каждой переменной.
не убывает по каждой переменной.
3.  непрерывна слева по каждой переменной.
непрерывна слева по каждой переменной.
4.  для любого i= 1, 2 ,…, n.
для любого i= 1, 2 ,…, n.
5.  если все n аргументов этой функции распределения стремятся к
если все n аргументов этой функции распределения стремятся к 
Отметим, что если только один из аргументов этой функции, скажем  стремится к бесконечности, то в пределе получится функция распределения случайного вектора, который получается из исходного вектора отбрасыванием компоненты
стремится к бесконечности, то в пределе получится функция распределения случайного вектора, который получается из исходного вектора отбрасыванием компоненты 
Говорят, что случайный вектор X имеет дискретное распределение, если он принимает конечное или счетное число значений. Для дискретного случайного вектора X, как и в случае дискретной случайной величины, можно ввести дискретную плотность распределения, определяемую равенством 
С помощью дискретной плотности распределения можно вычислять вероятности событий вида { Х  для любого n- мерного множества A. Действительно, P (Х
для любого n- мерного множества A. Действительно, P (Х  ) =
) = 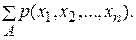 Здесь сумма распространяется на значения случайного вектора X, принадлежащие множеству A.
Здесь сумма распространяется на значения случайного вектора X, принадлежащие множеству A.
Дискретная плотность распределения обладает двумя очевидными свойствами:
1.  для всех значений случайного вектора X.
для всех значений случайного вектора X.
2.  где суммирование распространяется на все значения случайного вектора X.
где суммирование распространяется на все значения случайного вектора X.
Говорят, что n -мерный случайный вектор X имеет непрерывное (абсолютно непрерывное) распределение, если существует такая функция n переменных  , что функция распределения вектора X может быть представлена в виде
, что функция распределения вектора X может быть представлена в виде
 =
= 
Из этой формулы следует, что плотность распределения случайного вектора можно получить из его функции распределения с помощью формулы

При наличии плотности распределения смешанная производная n -го порядка существует.
Плотность распределения случайного вектора, как и плотность распределения случайной величины, обладает двумя определяющими свойствами: 1) она неотрицательна; 2) интеграл от нее по всему n -мерному пространству равен единице.
С помощью плотности распределения можно вычислять вероятности событий, связанных с данным случайным вектором, по формуле

Здесь A является множеством n -мерного пространства и для краткости записи знак  обозначает n -мерный интеграл.
обозначает n -мерный интеграл.
Случайные величины  , составляющие случайный вектор X, называются независимыми, если их совместную функцию распределения можно разложить в произведение функций распределения компонент вектора X, т. е.
, составляющие случайный вектор X, называются независимыми, если их совместную функцию распределения можно разложить в произведение функций распределения компонент вектора X, т. е.
 =
= 
Если случайный вектор X обладает дискретной или непрерывной плотностью распределения, то независимость его компонент равносильна свойству: совместная плотность распределения (непрерывная или дискретная) случайного вектора X равна произведению плотностей распределения компонент, т. е. 
Можно показать, что если некоторые случайные величины независимы, то независимы также и функции от них.
Рассмотрим вопрос о том, как из плотности распределения двумерного вектора получить плотность распределения его компонент.
В случае дискретного распределения двумерного вектора для дискретной плотности распределения его первой компоненты легко получить формулу  где суммирование распространяется на все значения случайной величины Y. Естественно, в непрерывном случае сумма заменяется интегралом, что приводит к формуле
где суммирование распространяется на все значения случайной величины Y. Естественно, в непрерывном случае сумма заменяется интегралом, что приводит к формуле  Здесь
Здесь  обозначает плотность распределения случайной величины X, p (x,y) обозначает совместную плотность распределения случайных величин X и Y. Эти соотношения естественным образом распространяются на векторы больших размерностей. ▲
обозначает плотность распределения случайной величины X, p (x,y) обозначает совместную плотность распределения случайных величин X и Y. Эти соотношения естественным образом распространяются на векторы больших размерностей. ▲
Задача 2.1. В ящике два шара, на каждом из которых написана цифра 1, и три шара, на каждом из которых написана цифра 2. Один за другим наудачу вынимают два шара. Пусть X – это номер на первом шаре, Y – номер на втором шаре. Найти совместную дискретную плотность распределения случайных величин X и Y и P (Y = 2).
Решение. Использовав формулу умножения вероятностей, получим

Поступая аналогично для вычисления других вероятностей, получим таблицу
| (x, y) | (1, 1) | (1, 2) | (2, 1) | (2, 2) |
| P ((X, Y) = (x, y)) | 1/10 | 3/10 | 3/10 | 3/10 |
P (Y = 2) = p (1, 2) + p (2, 2) = 3/5.
Задача 2.2. Из хорошо перемешанной полной колоды, состоящей из 36 карт, вытаскивают одну карту. Случайная величина X равна единице, если вытащенная карта красная, и равна нулю, если она черная. Случайная величина Y равна единице, если вытащенная карта туз, двойке, если она – король, и тройке, если вытащенная карта не является тузом или королем. Являются ли случайные величины X и Y независимыми?
Решение. Проверим определение независимости для случайных величин X и Y, а именно то, что  =
=  :
:

Таким образом,  .
.
Для других значений X и Y условие независимости проверяется аналогично.
Задача 2.3. X и Y независимые случайные величины, имеющие стандартное равномерное распределение. Найти плотность распределения p (x) случайной величины Z = max(X, Y).
Решение. Случайные величины X и Y имеют функцию распределения

В силу независимости случайных величин X и Y их совместная функция распределения  Далее,
Далее,

Чтобы найти плотность распределения случайной величины Z, достаточно продифференцировать это равенство. Таким образом,

Задача 2.4. Из единичного квадрата случайным образом выбирается точка. Ее координаты (A, B) рассматриваются как две случайные величины. Являются ли они независимыми случайными величинами? Рассмотрим квадратное уравнение  Найти вероятность того, что оно имеет вещественные корни.
Найти вероятность того, что оно имеет вещественные корни.
Решение. 
Отсюда следует, что  =
=  и, следовательно, случайные величины A и B независимы. Исследовав квадратное уравнение из условия задачи, придем к выводу, что оно имеет вещественные корни, если его дискриминант неотрицателен, т. е.
и, следовательно, случайные величины A и B независимы. Исследовав квадратное уравнение из условия задачи, придем к выводу, что оно имеет вещественные корни, если его дискриминант неотрицателен, т. е. 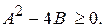 Поскольку точка (A, B) имеет равномерное распределение в единичном квадрате, то вероятность
Поскольку точка (A, B) имеет равномерное распределение в единичном квадрате, то вероятность  равна площади под графиком функции
равна площади под графиком функции  т. е. интегралу
т. е. интегралу 
Задача 2.5. Совместная плотностьраспределения случайных величин X и Y равна  Для других значений аргументов эта плотность равна нулю. Определить плотность распределения случайной величины X.
Для других значений аргументов эта плотность равна нулю. Определить плотность распределения случайной величины X.
Решение. Искомая плотность распределения для  равна
равна
