Математическая постановка задачи

ИНФОРМАЦИОННЫЕ ТЕХНОЛОГИИ

НА ТРАНСПОРТЕ

Методические указания

К выполнению СРС

для студентов направления 190700

дневной формы обучения

 

 

Саратов 2012

 

Задание выбирается соответственно номеру зачётной книжкистудента (подробнее рассмотрено ниже - в каждом из заданий).

Задание 1

Классическая транспортная задача

 

Оптовая фирма по продаже цемента имеет четыре склада, находящихся в разных р-нах г.Саратова, объёмы запасов на которых представлены на рис.1. Фирма обслуживает строительные организации, которые производят капитальный ремонт четырёх объектов, спрос которых также представлен на рис.1. Расстояния между складами и объектами строительства представлены в табл.1. Средняя стоимость перевозки 1 мешка с цементом на 1 км составляет 50 рублей.

Найдите с помощью Excel оптимальный план перевозки цемента между складами и объектами строительства, выбранными по своему варианту в табл.2 и 3.

 

 

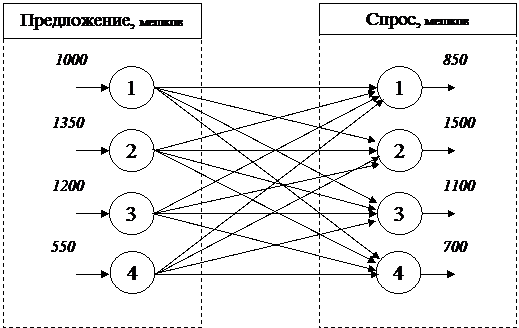Рис. 1. Объёмы спроса и предложения

 

 

Таблица 1

Кратчайшие расстояния, км

 

	Объекты строительства
Стадион	Театр	Бассейн	Школа
Склады		Волжский
	Ленинский
	Заводской
	Октябрьский

 

Таблица 2

Выбор поставщиков соответственно номеру зачётной книжки

 

Предпос-ледний номер зачётной книжки
Номера складов (поставщики)	1;2;3	2;3;4	1;2;4	1;3;4	1;2	2;3	3;4	1;4	2;4	1;2;3;4

 

Таблица 3

Выбор потребителей соответственно номеру зачётной книжки

 

Последний номер зачётной книжки
Номера объектов строитель-ства (потребители)	1;2;4	1;3;4	2;3;4	1;2;3	2;4	1;2	1;2;3;4	3;4	1;3	2;3

 

Математическая постановка задачи

В исследовании операций под транспортной задачей обычно понимают задачу выбора плана перевозок некоторого товара (изделий, груза) от m поставщиков (пунктов производства, поставщиков) к n потребителям (станциям назначения, пунктам сбыта), обеспечивающего минимальные транспортные затраты. При этом предполагают, что:

а) мощность i-го поставщика (объем поставок товара от i -го поставщика) равна S_i >0, i =1,..., m;

б) мощность j-го потребителя (объем поставок товара к j -му потребителю) равна D_j >0, j =1,..., n;

в) стоимость перевозки единицы товара (в условных денежных единицах) от i -го поставщика к j -му потребителю равна с_ij;

(1)

г) суммарная мощность всех поставщиков равна суммарной мощности всех потребителей:

Далее под объемом товара будем понимать его количество в фиксированных единицах измерения.

Для математического описания транспортной задачи вводят переменные x_ij, обозначающие объемы поставок товара от i -го поставщика к j -му потребителю. В этом случае x_i1+x_i2+...+x_in — общий объем поставок товара от i -го поставщика, т.е. мощность этого поставщика; x_1j+x_2j+...+x_mj — общий объем поставок товара к j-му потребителю, т.е. мощность этого потребителя; c₁₁x₁₁+c₁₂x₁₂+...+c_mnx_mn — суммарная стоимость перевозок товара от потребителей к поставщикам. С учетом этого рассматриваемая задача может быть представлена в следующем виде:

 

	(2а)
	(2б)
	(2д)

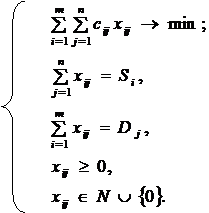На рис.2 показано представление транспортной задачи в виде сети с m пунктами отправления и n пунктами назначения, которые показаны в виде узлов сети. Дуги, соединяющие узлы сети, соответствуют маршрутам, связывающим пункты отправления и назначения. С дугой (i,j), соединяющей пункт отправления i с пунктом назначения j, соотносятся два вида данных: стоимость c_ij перевозки единицы груза из пункта i в пункт j и количество перевозимого груза x_ij. Объем грузов в пункте отправления i равен S_i, а объем грузов в пункте назначения j равен D_j. Задача состоит в определении неизвестных величин x_ij, минимизирующих суммарные транспортные расходы и удовлетворяющих ограничениям, накладываемым на объемы грузов в пунктах отправления (предложение) и пунктах назначения (спрос).

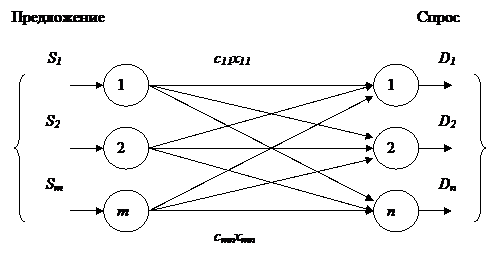
Когда суммарный объем предложений (грузов, имеющихся в пунктах отправления) не равен общему объему спроса на товары (грузы), запрашиваемые пунктами назначения, транспортная задача называется несбалансированной. В этом случае при решении классической транспортной задачи методом потенциалов применяют прием, позволяющий несбалансированную транспортную задачу сделать сбалансированной. Для этого вводят фиктивные пункты назначения или отправления. Выполнение баланса транспортной задачи необходимо для того, чтобы иметь возможность применить алгоритм решения, построенный на использовании транспортных таблиц.

	Рис. 2. Представление транспортной задачи в виде сети