БАРЬЕРНАЯ ЕМКОСТЬ p-n - ПЕРЕХОДА КАК ПРОЯВЛЕНИЕ ТОКОВ СМЕЩЕНИЯ

Барьерная емкость p-n - перехода проявляется при приложении к p-n - переходу изменяющегося во времени напряжения. При этом через p-n - переход проходит ток. Та доля тока, которая не связана с движением носителей заряда через p-n - переход, и определяет барьерную емкость.

Поэтому барьерная емкость должна быть связана с прохождением токов смещения. Для одномерного плоского p-n - перехода ток смещения одинаков во всех его сечениях:

,

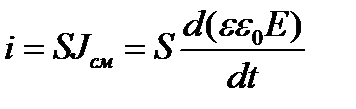где S – площадь p-n - перехода, Е – напряженность электрического поля, ε₀ – диэлектрическая постоянная, а ε – относительная диэлектрическая проницаемость кристалла полупроводника.

Полупроводник p – типа

Q

S

Рис. 3. К выводу выражения для барьерной емкости p-n - перехода

dn

E

Полупроводник n – типа

d

х

- dp

Значение тока смещения можно связать с изменением объемного заряда в p-n - переходе. Для этого мысленно выделим в p-n - переходе объем в виде цилиндра, образующие которого параллельны направлению электрического поля (рис.3). Пусть одно основание цилиндра совпадает с плоскостью х =0 металлургической границы между p и n -областями, а другое основание цилиндра лежит за пределами p-n - перехода. Тогда, согласно теореме Остроградского – Гаусса, можно определить поток вектора электрической индукции через поверхность, ограничивающую выделенный объем. Этот поток проходит только через одно основание цилиндра, так как боковые его поверхности параллельны электрическому полю, а второе основание лежит в области, где поле отсутствует. Следовательно,

εε₀ ES = Q,

где Q – заряд ионизированных примесей.

Ток смещения можно записать теперь таким образом:

,

где U – напряжение смещения, приложенное к p-n - переходу.

Сравнив последнее выражение с обычным выражением для тока через емкость, т. е. с

,

получаем, что в качестве барьерной емкости следует взять

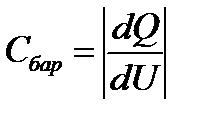. (1)

Абсолютное значение этого отношения взято потому, что объемный заряд в p-n - переходе может быть положительным и отрицательным, а правило знаков для напряжения выбрано произвольно.

ОБЩЕЕ СООТНОШЕНИЕ ДЛЯ БАРЬЕРНОЙ ЕМКОСТИ p-n - ПЕРЕХОДА

Исходя из определения барьерной емкости (1) можно получить общую формулу для барьерной емкости плоского p-n - перехода. Объемный заряд ионизированных примесей в цилиндре, выделенном в p-n - переходе,

,

где N (x) – распределение концентрации примесей вдоль оси х, q = ‑1.6·10^–19 Кл – величина заряда иона примеси.

Дифференциал этого объемного заряда можно определить путем дифференцирования по единственной переменной – нижнему пределу интегрирования:

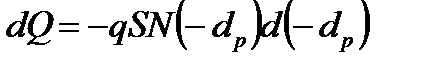. (2)

Дифференциал падения напряжения на p-n - переходе можно найти, продифференцировав выражение для полного падения потенциала на p-n - переходе (при обратном смещении перехода U <0):

.

Но при этом следует учесть, что переменными являются оба предела интегрирования. Поэтому целесообразно разбить интеграл на два, тогда каждый из них будет иметь по одному переменному пределу:

и

. (3)

Теперь, взяв отношение дифференциалов (2) и (3), получим

.

Для преобразования последнего выражения продифференцируем условие электрической нейтральности p-n - перехода:

,

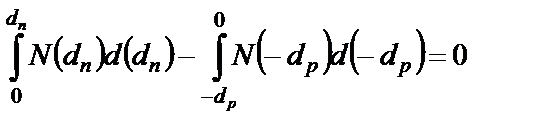т.е.

d (dp)

- dp

– dQ

Рис. 4. Изменение толщины p - n -перехода и объемного заряда при изменении напряжения на p - n - переходе

dn

dQ

d

х

d (dn)

.

Учтем, что d = d_p + d_n, тогда

. (4)

Таким образом, барьерная емкость плоского одномерного p-n -перехода может быть рассчитана по формуле плоского конденсатора. Такой результат не является очевидным, так как распределение зарядов в плоском конденсаторе и p-n - переходе неодинаково. Причина совпадения формул – в характере изменения объемного заряда p-n - перехода: при изменении напряжения на p-n - переходе заряд изменяется потому, что сдвигаются границы p-n - перехода. Заряды, обусловливающие барьерную емкость, сосредоточены в двух тонких слоях, расположенных на расстоянии d один от другого (рис.4), что очень напоминает поверхностные заряды на металлических обкладках конденсатора.

ХОД РАБОТЫ

1. Собрали установку согласно схеме на рис. 1.
В качестве исследуемого элемента подключили стабилитрон КС515А

2. Включили генератор и осциллограф, используя руководство по использованию.

3. Сопротивление R = 50 Ом.
При постоянном I_пр = 20 мА, изменяли величину тока обратносмещенного диода I _пр, изменяя напряжение U_­– от 8 до 2 В с шагом в 1 В. При этом измеряли t₁ и t_вос.

Результаты занесены в таблицу 1.

U–, В	Iобр, мА	t1, нс	tвос, нс	Q, 10-11 Кл	Сдиф, пФ
φ0, В
0,3	0,6	1,0
	0,157			4,79
	0,137			4,86
	0,118			4,26
	0,098			3,71
	0,078			3,15
	0,059			2,49
	0,039			1,85

 

4. Вычисляем заряд Q по формуле Q = I_обр(t₁+(t_вос–t₁)/2,3)

5. Оцениваем величину диффузной емкости C_диф≈Q/φ₀

 

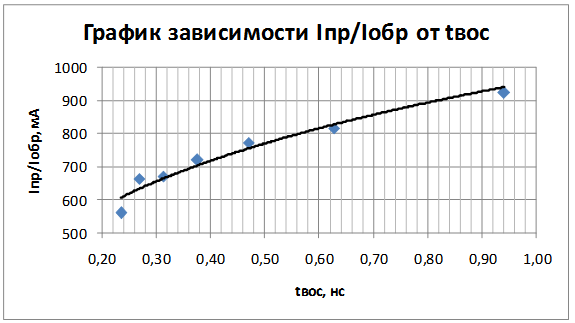
Рис. 2

 

 

в графиках следует изменить подписи к осям и название

Исследуемый элемент Диод КД2007

U–, В	Iобр, мА	t1, нс	tвос, нс	Q, 10-11 Кл	Сдиф, пФ
φ0, В
0,3	0,6	1,0
	0,157		1,04	2,22
	0,137		1,18	2,41
	0,118		1,39	2,47
	0,098		1,66	2,45
	0,078		2,28	2,53
	0,059		3,2	2,97
	0,039		4,48	2,84

Копия экрана наблюдаемой осциллограммы переходного процесса

 

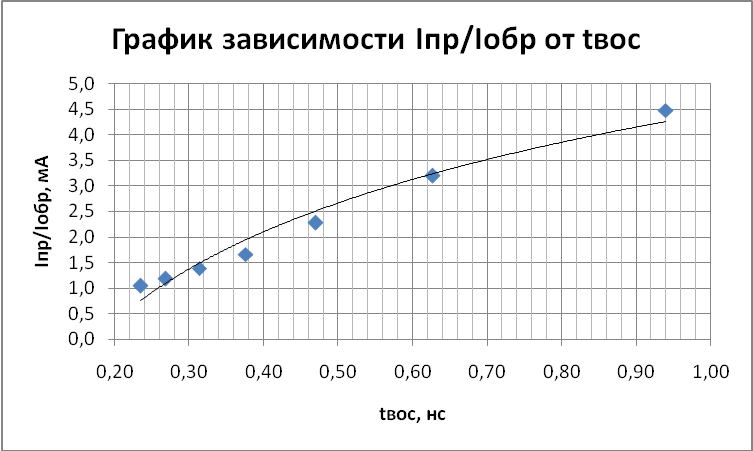
Вывод: изучили переходные процессы в полупроводниковых диодах.
Определили диффузионную емкость для стабилитрона КС515А и диода КД2007 и величины зарядов, накопленного на их базе.

Автор: Шаниязов Марат, 2012г.