Пусть по выборке случайной величины Х объема n необходимо проверить гипотезу Н0 о том, что Х имеет предполагаемый закон распределения. Рассмотрим решение этой задачи с помощью критерия согласия Пирсона.
Пусть построена гистограмма для заданной выборки случайной величины Х объема n с частичными интервалами одинакового размера h. Это значит, что для каждого частичного интервала Dj вычислены частоты nj попадания в него вариант выборки, где j = 1,..., N, N - число частичных интервалов. По форме гистограммы делается предположение о типе закона распределения и по выборке вычисляются точечные оценки его параметров. Используя предполагаемый закон распределения случайной величины Х, находим вероятности pj того, что значение Х принадлежит частичным интервалам Dj, то есть 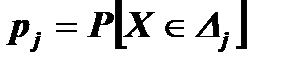 , где j = 1,..., N. Величины
, где j = 1,..., N. Величины 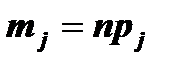 равны теоретическим частотам попадания случайной величины Х в каждый частичный интервал. Выборочное (наблюдаемое) значение статистики критерия вычисляется по формуле:
равны теоретическим частотам попадания случайной величины Х в каждый частичный интервал. Выборочное (наблюдаемое) значение статистики критерия вычисляется по формуле: 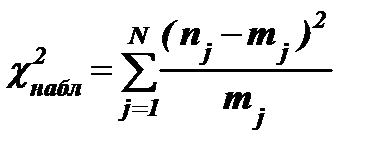 ~c2 (N – mp – 1) и имеет распределение c2 с N–mp–1 степенями свободы, где mp – число неизвестных параметров распределения, оцениваемых по выборке.
~c2 (N – mp – 1) и имеет распределение c2 с N–mp–1 степенями свободы, где mp – число неизвестных параметров распределения, оцениваемых по выборке.
Гипотеза Н0 согласуется с результатами наблюдений на уровне значимости α, если 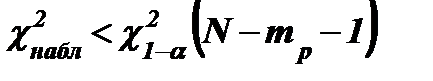 , где
, где 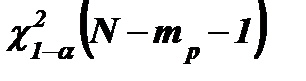 - квантиль порядка 1 – α распределения c2 с N–mp–1 степенями свободы. Если же
- квантиль порядка 1 – α распределения c2 с N–mp–1 степенями свободы. Если же 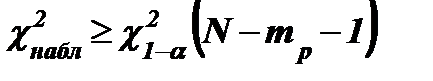 , то гипотеза Н0 отклоняется.
, то гипотеза Н0 отклоняется.
Замечание. Критерий c2 использует тот факт, что случайные величины 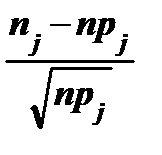 , j = 1, 2. …, N имеют распределение, близкое к нормальному нормированному N (0, 1). Чтобы это утверждение было достаточно точным, необходимо, чтобы для всех интервалов выполнялось
, j = 1, 2. …, N имеют распределение, близкое к нормальному нормированному N (0, 1). Чтобы это утверждение было достаточно точным, необходимо, чтобы для всех интервалов выполнялось 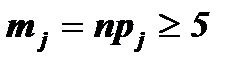 . Если для некоторых интервалов это условие не выполняется, то их следует объединить с соседними.
. Если для некоторых интервалов это условие не выполняется, то их следует объединить с соседними.
При проверке этой гипотезы в соответствии с критерием согласия Пирсона при заданном уровне значимости a используется следующий порядок расчета.
1) Для каждого частичного интервала определяются средние точки yj частичных интервалов:
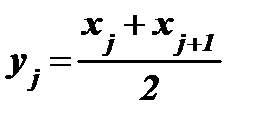 ,
,
 ,
,
где 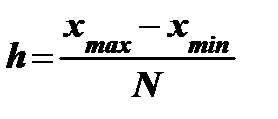 - длина частичного интервала, xmax, xmin - максимальная и минимальная варианты выборки, xj - точки, которыми интервал значений выборки (xmax;xmin) разбит на частичные отрезки, при этом x1 = xmin, xN+1 = xmax.
- длина частичного интервала, xmax, xmin - максимальная и минимальная варианты выборки, xj - точки, которыми интервал значений выборки (xmax;xmin) разбит на частичные отрезки, при этом x1 = xmin, xN+1 = xmax.
2) Вычисляются выборочные характеристики: выборочное среднее 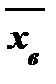 и исправленное выборочное среднее квадратическое отклонение s.
и исправленное выборочное среднее квадратическое отклонение s.
3) Вычисляются теоретические частоты предполагаемого распределения:
а) для равномерного закона по формуле:
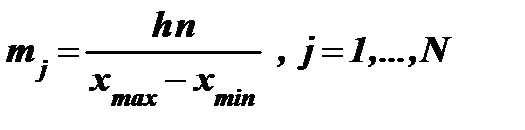 ,
,
то есть для всех частичных интервалов теоретические частоты одинаковы;
б) для нормального закона:
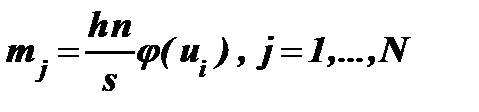 ,
,
где 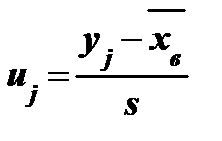 ,
, 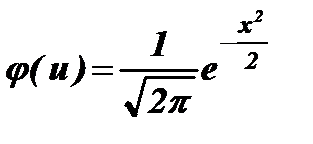 - плотность нормального нормированного распределения;
- плотность нормального нормированного распределения;
в) для показательного (экспоненциального) закона:
 ,
,
где lв - выборочный параметр показательного закона распределения:
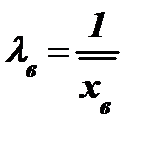 .
.
Находится наблюдаемое значение критерия c2:
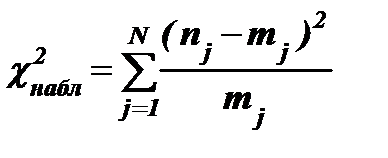 .
.
5) Находится критическое значение критерия c2 по уровню значимости a и числу степеней свободы k = N - mp - 1, где mp - число параметров распределения, равное mр = 2 для нормального и равномерного распределений, mp = 1 для показательного распределения: 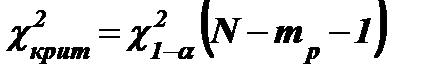 .
.
6) Правило проверки гипотезы: если 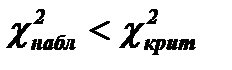 - то выдвинутая гипотеза о типе закона распределения не отвергается, если
- то выдвинутая гипотеза о типе закона распределения не отвергается, если 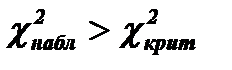 - то отвергается.
- то отвергается.