Цель работы
Измерение радиуса кривизны линзы и определение длины световой волны.
Темы для изучения
Интерференция световых волн в тонких пленках, кольца Ньютона (полосы равной толщины). Когерентность световых волн, оптическая разность хода и ее роль в явлении интерференции.
Область применения
Оптическое приборостроение, метод оптического контроля поверхностей: проверка плоско-параллельности, сферичности и толщины.
Экспериментальная установка и порядок ее настройки
Установка для получения колец Ньютона показана на рис1.
Закрепите ртутный фонарь высокого давления с двойным конденсором (фокусное расстояние 60 мм), держатель для линз с интерференционным фильтром, устройство для получения колец Ньютона, держатель для линз с линзой с фокусом 50 мм и полупрозрачный экран на расстоянии 40 см от линзы на оптической скамье.
В начале эксперимента отрегулируйте траекторию хода лучей, сначала без светофильтров, чтобы на экране можно было наблюдать четкие кольца интерференции.
Затем в держатель для линзы вставьте желтый светофильтр. При помощи трех регулировочных винтов на устройстве для получения колец Ньютона установите плосковыпуклую линзу на плоскопараллельной стеклянной пластине так, чтобы светлый центр колец интерференции находился в средней точке миллиметровой шкалы, спроецированной на экран. В процессе регулировки убедитесь, что линза и стеклянная пластина только прикасаются друг к другу.
Определите радиусы колец Ньютона 
для трех различных интерференционных фильтров в порядке, указанном преподавателем.
В экспериментальной установке значение радиуса кривизны плосковыпуклой линзы R = 12,1 м. Эти данные целесообразно использовать для контроля точности выполненных измерений R и 
.
|
|
Рис. 1: Экспериментальная установка Кольца Ньютона для определения длины волны.
Теория метода
Если на стеклянную пластинку положить плоско-выпуклую линзу, то между ними возникнет тонкая воздушная прослойка, утолщающаяся от точки касания к краям линзы.
Если на эту систему приблизительно нормально к поверхности пластинки падает пучок монохроматического света, то световые волны, отраженные от нижней и верхней границ этой воздушной прослойки, будут интерферировать (рис.2). Результат интерференции зависит от разности хода между интерферирующими лучами, которая, в свою очередь, определяется толщиной воздушной прослойки. Так как места равной толщины воздушной прослойки представляют собой концентрические окружности с центром в точке касания линзы и пластинки, то и интерференционная картина имеет вид концентрических колец, которые обычно называют кольцами Ньютона (полосы равной толщины).
Рис. 2: Построение интерференционной картины колец Ньютона в отраженном свете
Вычислим разность хода интерферирующих лучей. Волна, отраженная от нижней поверхности прослойки с толщиной d, пройдет путь на 2d больший, чем волна, отраженная от верхней поверхности прослойки. К этой разности хода надо прибавить половину длины волны, так как отражение от более плотной среды (граница воздух-стекло) происходит со скачкообразным изменением фазы на p. При отражении от менее плотной среды (граница стекло-воздух) такого изменения фазы не происходит.
|
|
Итак, разность хода между интерферирующими волнами составляет
. (1)
Нетрудно показать, что толщина воздушной прослойки d связана с радиусом кольца r и радиусом кривизны линзы R соотношением[1]
. (2)
В точках, для которых разность хода
, (3)
где k – целое число, наблюдается максимум освещенности – светлое интерференционное кольцо.
Из формул (1), (2) и (3) следует, что радиус k-го светлого кольца в отраженном свете
, (4)
Аналогично для темных интерференционных колец разность хода равна
, (5)
и радиус k-го темного кольца в отраженном свете
. (6)
По формулам (4) или (6) можно определить радиус кривизны линзы R, если известна длина волны l, или наоборот – определить длину волны, если известен радиус кривизны линзы.
В настоящем эксперименте кольца Ньютона создаются в проходящем свете (рис. 3).
Интерференционная картина, как и в отраженном свете, создается лучами 1 и 2. Причем, луч 2 дважды отражается от границы воздух-стекло, что приводит к изменению фазы волны на 2p.
Толщина слоя воздуха на расстоянии 
от точки соприкосновения линзы и пластины составляет 
, так как идеальное соприкосновение между поверхностями может отсутствовать. Поэтому, с учетом зазора 
между линзой и стеклянной пластиной, разность хода интерферирующих лучей 1 и 2 равна:
.
   |
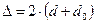Рис. 3: Ход лучей, формирующих интерференционную картину в проходящем свете.
Условие максимума интенсивности для колец Ньютона в проходящем свете имеет вид
(7)
И для радиуса светлых колец в проходящем свете справедливо соотношение
|
|
(8)
Для удобства дальнейших расчетов рекомендуем построить график зависимости 
от k (рис. 4).
Рис. 4: Зависимость радиуса колец Ньютона от их номера (порядка) k при разной длине волны.
В проходящем свете для заданного значения радиуса кривизны линзы 
, длина волны 
рассчитывается из тангенса угла наклона прямой 
:
Для определения радиуса кривизны линзы используется желтый фильтр с длиной волны 
582 ± 4 нм.