Расширенная формулировка Планка
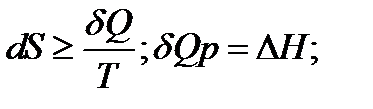
При изменение температуры от Т1 до Т2 изменение энтропии можно выразить следующим образом:
;
При помощи этого уравнения можно получить абсолютное значение энтропии вещества. Отметим существенное отличие абсолютных значений энтропии от значения других характеристических функций (∆U,∆H,∆G и ∆F), которые являются разностью двух состояний, а не абсолютными значениями.
При абсолютном нуле способность системы к рассеянию энергии иссекает; например, у совершенного
кристалла при абсолютном нуле все атомы находятся в регулярном однородном состояние без разупорядогенности. Они фиксированы в узлах кристаллической решетки и лишены возможности совершать какое - либо движение.
1. Первая строгая формулировка Планка:
Энтропия правильно образованного кристалла при Т=0К равна 0.
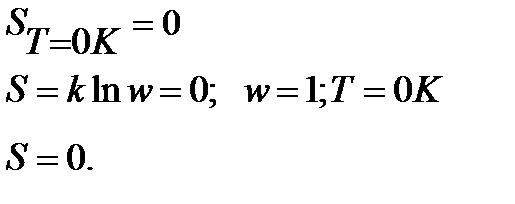
Подчеркнем, что речь идет о правильно образованном, бездефектном, совершенном кристалле. Большинство реальных кристаллов содержат примеси, имеют дефекты, а их энтропия даже при абсолютном нуле несколько больше нуля.
2. Можно показать, что энтропия равна:
По мере приближения к абсолютному нулю, когда Т→0, теплоёмкость становиться бесконечно малой величиной и стремится к нулю. Тогда подынтегральное выражение в правой части управления (1) в результате деления двух бесконечно малых величин становится неопределённым, а само уравнение теряет смысл. Из этого в свою очередь вытекает следствие о недостижимости абсолютного нуля температуры. У каждого тела существует своя критическая температура, ниже которой охладить тело невозможно.
РАСЧЕТ АБСОЛЮТНОГО ЗНАЧЕНИЯ ЭНТРОПИИ
Третий закон термодинамики используется для вычисления абсолютных энтропий простых и сложных веществ. Абсолютной энтропией называется энтропия, отсчитанная относительно абсолютного нуля температуры S(0)=0.
|
|
Для расчетов необходимо учитывать следующие уравнения.
1. 
2. 
3. 
Если вещество может находиться в различных агрегатных состояниях, то следует учитывать изменение энтропии при фазовых переходах. Тогда в общем случае для вещества в газообразном состоянии абсолютная энтропия будет складываться из следующих составляющих:
По этому уравнению можно вычислить абсолютные энтропии веществ в твердом, жидком и газообразном состояниях.
Пример. Рассчитать энтропию воды при t=1500C.
Энтропия воды при t=1500C(423К) равна: 
;
;
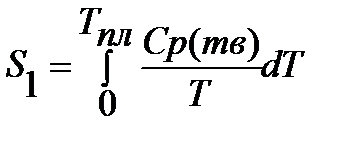Третий закон термодинамики можно использовать для расчета химических равновесий.
РАСЧЕТ КОНСТАНТЫРАВНОВЕСИЯ КР:
I. По табличным значениям.
II. Интегрирование изобары Вант-Гоффа.
III. Метод комбинированных равновесий.
I. По табличным значениям.
В настоящее время известны стандартные теплоты образования ∆Н0f и энтропия S0298, более 7500 простых веществ и соединений. С помощью этих табличных значений можно вычислить термодинамические параметры (∆Н0298,∆S0298 и ∆G0298) многих десятков тысяч реакций, в том числе предполагаемых и не изученных экспериментально. В методе расчета, основанном на использовании стандартных термодинамических величин, используются два исходных уравнения:
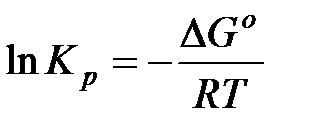
а также уравнения для процессов:
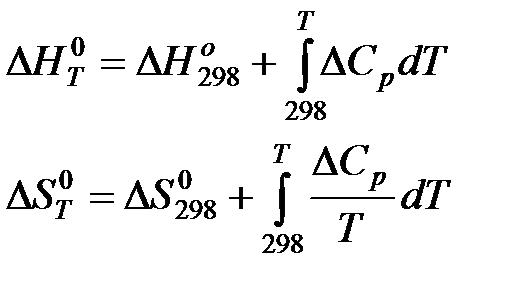
Расчет ΔG при заданной температуре.
а) Первое приближение Улиха.
(грубое приближенное уравнение )
|
|
Данное приближение решение необходимо для быстрой оценки возможности реакции при интересующей нас температуре и положения равновесия.
б) Второе приближение Улиха.
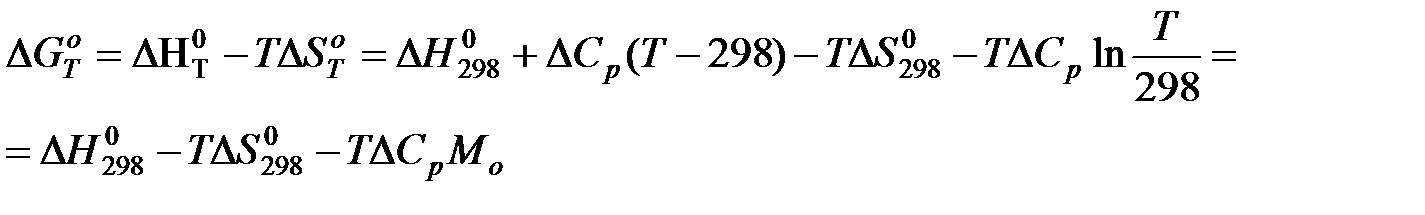
Где 
Второе приближение используется в случае, если не требуется особой точности в определении положения равновесия.
в) Метод Шварцмана-Темкина.
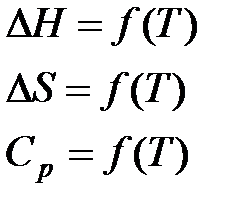
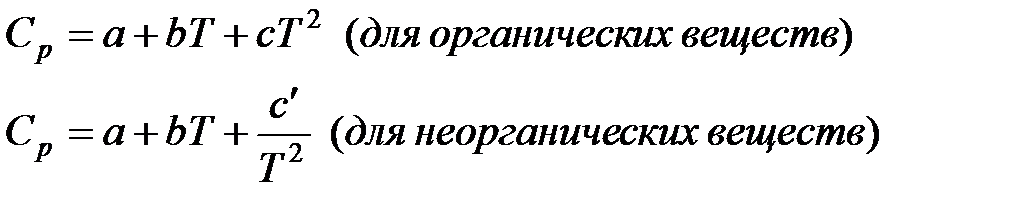
Проведем первое интегрирование уравнения и получим:
Проведем второе интегрирование и, собрав все члены с общими множителями 
, будем иметь:
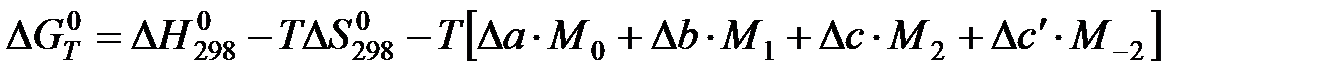
АЛГОРИТМ РАСЧЕТА Кр
1.Составляем таблицу термодинамических величин: aA + bB ↔ cC + dD
| Вещество | ∆Н0f, Дж/(моль*К) | S0298, Дж/(моль*К) | Ср, Дж/(моль*К) | а | b | c |
| А | ||||||
| В | ||||||
| С | ||||||
| D |
2.проводим расчет т.д. параметров при стандартных условиях:
∆Н0298 =∑(ni∆Н0f)кон — ∑(ni∆Н0f)нач;
∆ S0298=∑(ni S0298)кон — ∑(ni S0298)нач;
∆Ср=∑(ni Ср)кон — ∑(ni Ср)нач;
∆a=∑(ni a)кон — ∑(ni a)нач;
∆b=∑(ni b)кон — ∑(ni Ср)нач;
∆c=∑(ni c)кон — ∑(ni c)нач.
3.Расчет изменения энергии Гиббса 
:
а) при стандартных условиях:
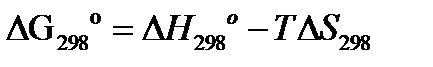
б) при интересующей нас температуре Т
(а) по первому приближению Улих;.
б) Второму приближение Улих;.
в) Метод Шварцмана-Темкина)
4. Расчет константы равновесия Кр:
