План лекції №1:
| 1.1. Кинематика поступательного и вращательного движения 1.1.1. Предмет механики 1.1.2. Механическое движение. Модели в механике 1.1.3. Определение положения точки в пространстве. Траектория. Путь. Перемещение 1.1.4. Скорость 1.1.5. Ускорение. Нормальное и тангенциальное ускорение 1.1.6. Скорость и путь при поступательном движении 1.1.7. Кинематические характеристики вращательного движения: угловая скорость и угловое ускорение 1.1.8. Связь между линейной и угловой скоростью, линейным и угловым ускорением Задания и вопросы для самоконтроля |
1. МЕХАНИКА
1.1. Кинематика поступательного и вращательного движения
1.1.1. Предмет механики
Механикой называется раздел физики, в котором изучаются закономерности механического движения и причины, вызывающие или изменяющие это движение. Механика делится на три раздела: кинематику, динамику и статику.
Кинематика изучает движение без учета причин, его вызывающих.
Динамика изучает движение с учетом причин, его вызывающих.
Статика - наука о равновесии.
Существует классическая, релятивистская и квантовая механика.
Классическая механика изучает движение макроскопических тел со скоростями, много меньшими скорости света в вакууме (v<<c, c=3·108м/c).
Релятивистская механика (или теория относительности) изучает движение тел со скоростями, соизмеримыми со скоростью света в вакууме.
Квантовая механика изучает движение микрочастиц (отдельные атомы, элементарные частицы). Изучение нашего курса начнем с классической механики.
1.1.2. Механическое движение. Модели в механике
Механическим движением называется процесс изменения взаимного расположения тел или их частей в пространстве и с течением времени. Для описания движения в механике используются физические модели. Простейшими моделями в механике являются материальная точка и абсолютно твердое тело.
Материальной точкой называется обладающее массой тело, размерами которого можно пренебречь в условиях данной задачи. Например, при вычислении траектории, по которой Земля движется вокруг Солнца, Землю можно рассматривать как материальную точку, так как ее радиус в 24 000 раз меньше радиуса ее орбиты. При рассмотрении движения тел по поверхности Земли она должна рассматриваться как протяженный объект.
Любое тело можно рассматривать как совокупность материальных точек.
Абсолютно твердым телом называется тело, деформациями которого можно пренебречь в условиях данной задачи.
Тело может двигаться поступательно и вращательно.
Поступательным движением называется такое движение, при котором любая прямая, проведенная в теле, остается параллельной самой себе. При поступательном движении все точки тела движутся одинаковым образом. Поэтому достаточно рассмотреть движение одной точки тела, например, центра тяжести, чтобы говорить о движении тела в целом.
Вращательным движением называется движение, при котором все точки тела описывают окружности. Центры этих окружностей лежат на прямой, называемой осью вращения. В общем случае движение твердого тела можно представить как результат сложения поступательного и вращательного движений.
1.1.3. Определение положения точки в пространстве.Траектория. Путь. Перемещение
Для того чтобы описывать движение материальной точки, надо ввести систему отсчета. Системой отсчета называется совокупность системы координат и часов, связанных с телом, по отношению к которому изучается движение.
Положение точки в пространстве можно описать двумя способами:
1) векторным, т. е. задать радиус-вектор  . Радиус-вектором называется вектор, проведенный из начала координат в данную точку; 2) координатным - задать три координаты - x,y,z (рис. 1.1).
Рис.1.1
Модуль радиус-вектора вычисляется по теореме Пифагора
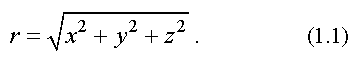При перемещении точки в пространстве она описывает некоторую кривую, называемую траекторией материальной точки.
Расстояние, отсчитанное вдоль траектории, представляет собой длину пути ΔS (рис. 1.2) или просто пройденный путь.
Рис.1.2
Перемещением называется вектор  , соединяющий начальное и конечное положение материальной точки (рис. 1.2). Вектор перемещения показывает откуда и куда переместилась точка.
Перемещение , скорость  , ускорение  являются кинематическими характеристиками движения материальной точки, а также кинематическими характеристиками поступательного движения абсолютно твердого тела.
1.1.4. Скорость
Скорость характеризует направление и быстроту перемещения точки или тела в пространстве.
Средней скоростью называется отношение перемещения к промежутку времени, за которое это перемещение произошло
Средняя скорость направлена так же, как вектор перемещения  (рис. 1.3).
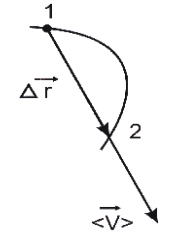Рис.1.3
Модуль средней скорости равен  .
Скоростью (или мгновенной скоростью) материальной точки называется предел отношения ее перемещения к промежутку времени, за которое это перемещение произошло, при бесконечном убывании промежутка времени, т. е.
В математике такой предел называется производной. Скорость равна производной от радиус-вектора по времени
Скорость направлена по касательной к траектории, так как при  сливается с касательной (рис. 1.4).
Рис.1.4
При  , поэтому  .
Модуль скорости равен производной от пути по времени:
|
1.1.5. Ускорение. Нормальное и тангенциальное ускорение
Ускорение характеризует быстроту изменения скорости. Среднее ускорение вычисляется как отношение изменения скорости к промежутку времени, за которое это изменение произошло
Мгновенным ускорением (или просто ускорением) называется предел отношения изменения скорости к промежутку времени при бесконечном убывании промежутка времени
Иначе, ускорение равно производной от скорости по времени
Ускорение может быть направлено под любым углом к скорости (рис. 1.5).
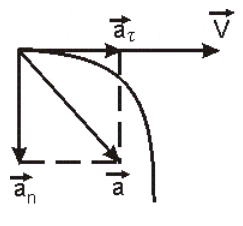Рис.1.5
Ускорение может быть разложено на две взаимно перпендикулярные составляющие: нормальное  и тангенциальное  .
Нормальное ускорение характеризует изменение скорости по направлению. Оно перпендикулярно к скорости 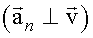 (см. рис. 1.5). Модуль нормального ускорения вычисляется как
где R - радиус кривизны траектории.
Тангенциальное ускорение определяет быстроту изменения скорости по величине (т. е. по модулю). Оно параллельно скорости  , если движение ускоренное, и противоположно скорости  , если движение замедленное.
Модуль тангенциального ускорения вычисляется как производная от модуля скорости по времени
Модуль полного ускорения вычисляется по теореме Пифагора
В зависимости от значений и движение классифицируется по траектории и ускорению. Например, при  и  - это равномерное прямолинейное движение, при  - это ускоренное криволинейное движение.
1.1.6. Скорость и путь при поступательном движении
Приведем формулы вычисления длины пути и скорости при равномерном и равнопеременном движении.
1. Равномерным движением называется движение, при котором скорость по модулю не изменяется.
При равномерном движении
 .
2. Равнопеременным движением называется движение с постоянным по модулю ускорением.
При равнопеременном движении
 ,
где S=x-x0, V0 - начальная скорость. Знак "+" - при равноускоренном движении. Знак "-" - при равнозамедленном движении.
1.1.7. Кинематические характеристики вращательного движения. Угловая скорость и угловое ускорение
При вращательном движении все точки тела описывают окружности, при этом радиус-векторы поворачиваются на угол  за время  . Для того, чтобы указать, в какую сторону совершается поворот, элементарные повороты изображают в виде вектора  . По модулю  равен величине угла поворота, а направление подчиняется правилу правого винта (рис. 1.6). Быстроту вращения характеризует угловая скорость  .
Рис.1.6
Угловой скоростью называется производная от угла поворота по времени. Модуль угловой скорости равен
Вектор угловой скорости направлен вдоль оси вращения по правилу правого винта (рис. 1.6). При равномерном вращении угловая скорость  связана с периодом обращения Т и частотой вращения  следующим образом
Модуль угловой скорости выражается в радианах в секунду (рад/с). Быстрота изменения угловой скорости характеризуется угловым ускорением  .
Угловым ускорением называется производная от угловой скорости по времени. Модуль углового ускорения равен
При вращении тела вокруг неподвижной оси угловое ускорение также как и угловая скорость направлено вдоль оси вращения. При ускоренном движении эти вектора сонаправлены  , при замедленном - противоположны  . Угловое ускорение измеряется в рад/с2.
При равномерном вращении
 .
При равнопеременном вращении
где  - начальная угловая скорость. Знак "+" - при равноускоренном движении. Знак "-" - при равнозамедленном движении.
1.1.8. Связь между линейной и угловой скоростью, линейным и угловым ускорением
При вращении твердого тела вокруг неподвижной оси линейные скорости и линейные (тангенциальные) ускорения  для различных его точек будут различны. Угловая скорость и угловое ускорение будут одинаковыми для всех точек вращающегося тела.
Для того чтобы найти связь между модулями линейной и угловой скорости нужно использовать известное в геометрии соотношение между центральным углом  и дугой, на которую он опирается (рис. 1.6)
 .
Отсюда:
 .
Используя формулы (1.5) и (1.12), получим
Формула (1.15) показывает, что линейная скорость равна угловой, умноженной на радиус.
Чтобы найти связь между модулями линейного (тангенциального) и углового ускорений, продифференцируем формулу (1.15)
Воспользуемся формулами (1.10) и (1.14) и получим
Из формулы (1.16) следует, что линейное (тангенциальное) ускорение равно угловому, умноженному на радиус.
Задания и вопросы для самоконтроля
1. На какие разделы делится механика?
2. Какие простейшие модели используются в механике?
3. Что называется поступательным движением? Вращательным?
4. Как определяют положение точки в пространстве?
5. Чем отличаются путь и перемещение?
6. Какие Вы знаете кинематические характеристики поступательного движения? Дайте определение скорости, ускорения.
7. Что характеризует нормальное ускорение? Что тангенциальное? Как они вычисляются?
8. Как вычисляются скорость и путь при поступательном движении?
9. Расскажите о кинематических характеристиках вращательного движения. Дайте определение угловой скорости и углового ускорения.
10. Как связаны линейные и угловые характеристики?
|