Фильтры нижних частот на ИНУН

 

Схема на ИНУН, реализующая функцию фильтра нижних частот Баттерворта или Чебышева второго порядка вида

 

 

изображена на рис. 1.6. Анализируя эту схему, получаем:

 

;

 

; (1.4)

 

.

 

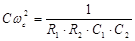Значения сопротивлений определяются следующим образом:

;

 

;

 

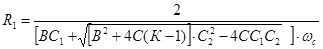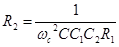; (1.5)

 

.

 

где С₂ имеет предпочтительно близкое к значению 10/f_с мкФ.

А С₁ должно удовлетворять следующему неравенству

 

 

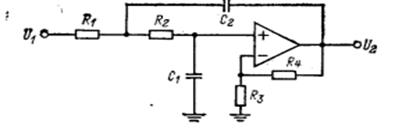
Рис. 1.6. Схема фильтра нижних частот на ИНУН

 

Расчет фильтра нижних частот на Инун

 

Для расчета фильтра нижних частот или Чебышева более высокого порядка, обладающего заданной частотой среза f_с (Гц), или w_с =2πf_с и коэффициентом усиления К = 1, необходимо выполнить следующие шаги.

1. Найти нормированные значения коэффициентов нижних частот В и С из соответствующей таблицы в приложении А.

2. Выбрать номинальное значение емкости С₂ (предпочтительно близкое к значению 10/f мкФ) и вычислить значения сопротивлений по (1.5)

3. Выбрать номинальные значения, наиболее близкие к вычисленным значениям, и реализовать фильтр или его звенья в соответствии со схемой, показанной на рис. 1.6.

 

 

Техническое задание

 

1. Фильтр Чебышева верхних частот на ИНУН;

2. Порядок N = 6;

3. Коэффициент усиления К = 8;

4. Частота среза f_c = 100 Гц;

5. Неравномерность передачи в полосе пропускания PRW = 1.0 дБ;

6. Использование резисторов и конденсаторов ряда Е96.

 

 

Расчеты

 

Один из популярных способов построения фильтра заключается в том, чтобы представить передаточную функцию в виде произведения сомножителей H1, H2,…, Нm и создать схемы или звенья, или каскады N1, N2,…, Nm, соответствующие каждому сомножителю. Эти звенья соединяются между собой каскадно, выход первого является входом второго и т.д. Если эти звенья не будут влиять друг на друга и не будут изменять собственные передаточные функции, то общая схема обладает требуемой передаточной функцией n-го порядка.

Разобьем фильтр 6-ого порядка на 3 звена 2-ого порядка. Так как общий коэффициент усиления должен быть равен 8, то все наши звенья будут одинаковы с коэффициентом усиления 2 каждое.

Каждое звено будет иметь передаточную функцию вида

 

 

Нормированные значения коэффициентов В, С из приложения А (в книге Д. Джонсон, Дж. Джонсон «Справочник по активным фильтрам») для параметров: общий порядок N = 6, неравномерности передачи, в полосе пропускания PRW = 1,0 дБ.

 

	В	С
I звено	0.124362	0.990732
II звено	0.339763	0.55772
III звено	0.464125	0.124707

 

Расчет первого звена

Порядок звена равен N = 2. Коэффициент усиления К₁ = 2.

1) Найдем нормированные значения коэффициентов В, С из приложения А (в книге Д. Джонсон, Дж. Джонсон «Справочник по активным фильтрам»).

 

	В	С
I звено	0.124362	0.990732

 

2) Вычисляем значение элементов C₁, C₂, R₁, R₂, R₃, R₄, по формулам:

Находим значение емкости С₂ близкое к величине , т.е. С₂ = 0.1 мкФ.

 

;

 

;

 

;

 

 

Откуда получаем теоретические значение элементов для первого звена

	С1, нФ	R1, кОм	R2, кОм	R3, кОм	R4, кОм
Теоретические значения элементов для I звена			0.995

 

Из уравнений

 

;

;

 

.

 

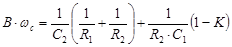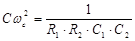Находим коэффициенты для передаточной функции

 

 

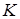
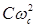
I звена		78.137

 

С учетом того, что 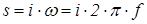определяем передаточную функцию первого звена

 

 

Таким образом, 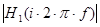– модуль передаточной функции – АЧХ первого звена, а – аргумент передаточной функции – ФЧХ первого звена.

АЧХ первого звена

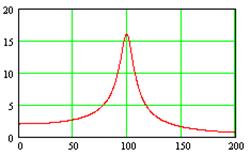
ФЧХ первого звена

Расчет второго звена

Порядок звена равен N = 2. Коэффициент усиления К₂ = 2

1) Найдем нормированные значения коэффициентов В, С из приложения А (в книге Д. Джонсон, Дж. Джонсон «Справочник по активным фильтрам»).

 

	В	С
II звено	0.339763	0.55772

 

2) Вычисляем значение элементов C₁, C_2, R₁, R₂, R₃, R₄, по формулам:

 

	С1, нФ	R1, кОм	R2, кОм	R3, кОм	R4, кОм
Теоретические значения элементов для II звена		93.69	4.6	196.6	196.6

 

Из уравнений находим коэффициенты для передаточной функции

 

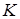
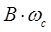
II звена		213.473

 

Подставляя данные коэффициенты в получаем передаточную функцию для второго звена

 

 

Таким образом, – модуль передаточной функции – АЧХ второго звена, а 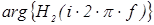– аргумент передаточной функции – ФЧХ второго звена.

 

АЧХ второго звена

 

ФЧХ второго звена

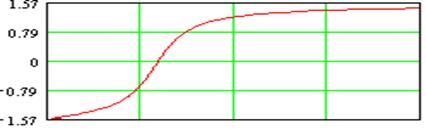
Расчет третьего звена

Порядок звена равен N = 2. Коэффициент усиления К₃ = 2

2) Найдем нормированные значения коэффициентов В, С из приложения А (в книге Д. Джонсон, Дж. Джонсон «Справочник по активным фильтрам»).

 

	В	С
III звено	0.464125	0.124707

 

2) Вычисляем значение элементов C₁, C_2, R₁, R₂, R₃, R₄, по формулам:

 

	С1, нФ	R1, кОм	R2, кОм	R3, кОм	R4, кОм
Теоретические значения элементов для III звена		68.58	20.68	178.5	178.5

 

Из уравнений находим коэффициенты для передаточной функции

 

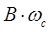
III звена		291.61

 

Подставляя данные коэффициенты в получаем передаточную функцию для второго звена

 

 

Таким образом, – модуль передаточной функции – АЧХ второго звена, а – аргумент передаточной функции – ФЧХ второго звена.

 

АЧХ третьего звена

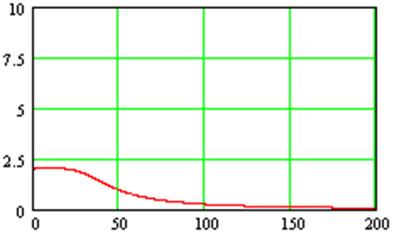
ФЧХ третьего звена

 

Итоговая передаточная характеристика будет представлять собой произведение сомножителей H1, H2, Н3: