Кристалл турмалина толщиной 1 мм пропускает только необычный луч и поглощает обычный. Пластинка турмалина может быть поляризатором. Недостатком таких пластин является селективное поглощение и необычного луча. Плоско-поляризованый свет, который проходит через турмалин, окрашивается в желто-зеленый цвет. Это сильно ограничивает применение кристаллов турмалина в качестве поляризационного приспособления
2.
Рассматривая различные плоскости, например в о. ц. к. решетке, можно легко заключить, что они заполнены атомами с различной плотностью. Свойства отдельно взятого кристалла (монокристалла) по данному направлению отличаются от свойств в другом направлении и, естественно, зависят от того, сколько атомов встречается в этом направлении. Различие свойств в зависимости от направления испытания носит название анизотропии. Все кристаллы анизотропны.
ДВОЙНОЕ ЛУЧЕПРЕЛОМЛЕНИЕ, раздвоение светового луча при прохождении через анизотропную среду. Открыто в 1670 датским физиком Э. Бартолином на кристалле исландского шпата (CaCO3). В некоторых кристаллах, например турмалине, каждый из раздвоенных лучей поглощается по-разному в разных направлениях, что приводит к различной окраске (дихроизму). Двойное лучепреломление может быть естественным и наведенным - под действием электрического поля, магнитного, поля упругих сил.
Луч света, падающий на поверхность кристалла, раздваивается в нем на два преломленных луча. Один из них подчиняется законам преломления света и называется обыкновенным лучом (о). Второй луч называют необыкновенным и обозначают (е). В общем случае он не лежит в плоскости падения и не подчиняется законам преломления.
|
|
Оптическая ось кристалла — направление в кристалле, вдоль которого не происходит двойного лучепреломления.
Всякая плоскость, проходящая через оптическую ось, называется главным сечением или главной плоскостью кристалла.
3.
Условия наблюдения интерференции света
-Когерентность двух волн в простейшем случае означает, что разность фаз между ними сохраняется постоянной или изменяется достаточно медленно. При сложении таких волн можно наблюдать четкую интерференционную картину. Когерентные волны получаются при помощи лазерных источников света, в которых работает механизм вынужденного излучения света.
-Длина когерентности должна быть больше оптической разности хода лучей
Бизеркало Френеля.
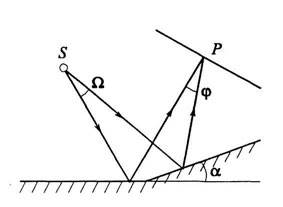
бизеркало Френеля (1816 г.). Свет от источника S отражается от двух зеркал, расположенных под достаточно малым углом 
. Волны, падающие на экран, могут рассматриваться как волны от двух мнимых изображений источника S в обоих зеркалах. При изменении положения точки наблюдения P на экране изменяется разность хода 
, в результате чего возникает система интерференционных полос, ширина которых зависит от угла схождения лучей 
.
Зеркало Ллойда
Прямой пучок света от источника S интерферирует с пучком, отражённым от зеркала под углом, близким к прямому. Таким образом, источниками когерентных волн являются источник S и его мнимое изображение в зеркале 
. При расчёте интерференционной картины следует учитывать характер отражениясвета от поверхности зеркала.
Расположение Юнга
В опыте Юнга источником света служит ярко освященная щель S, от которой световая волна падает на две узкие щели S1 и S2, освещаемые, таким образом, различными участками одного и того же волнового фронта. Световые пучки, проходящие через узкие щели S1 и S2, расширяются в результате дифракции и частично перекрываются, создавая интерференцию. Ввиду общности происхождения эти пучки когерентны. На экране в месте перекрытия пучков наблюдались параллельные полосы. Юнг первый наблюдал осуществленное таким образом явление интерференции (1802 г.) и первый установил принцип сложения амплитуд, объяснив это явление. 
|
|
Бипризма Френеля
Бипризма Френеля состоит из двух одинаковых, сложенных основаниями призм с малыми преломляющими углами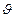 
(порядка нескольких минут). Параллельно этому основанию на расстоянии 
от него располагается источник света S. Свет от источника преломляется в обеих призмах, в результате чего за бипризмой распространяются световые пучки, как бы исходящие из мнимых источников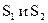 
, являющихся когерентными. На экране происходит наложение когерентных световых пучков и наблюдается интерференция.
Так как преломляющий угол бипризмы 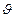очень мал и малы углы падения световых лучей на бипризму, можно считать, что углы отклонения лучей 
, падающих на верхнюю и нижнюю половинки бипризмы малы, а мнимые изображения источника света и сам источник расположены практически в одной плоскости:
.
Расстояние между источниками равно
sin 
.
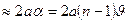Расстояние от источников до экрана:
.
Для наблюдения широких полос интерференции необходимо обеспечить малое расстояние 
= 
, при этом поле интерференции оказывается малым.
|
|
4.
Дифракция света – это совокупность явлений, заключающиеся в перераспределении светового потока при прохождении световой волны в средах с резкими неоднородностями. В узком смысле дифракция – это огибание волнами препятствие. Присутствие дифракции приводит к нарушению законов геометрии оптики, в частности – законов прямолинейного преломления.
Между дифракцией и интерференцией нет разницы, т.к. оба явления приводят к распределению световой волны. Различают дифракцию Фраунгофера и дифракцию Френеля.
Дифракция Фраунгофера – дифракция параллельных лучей. Наблюдается когда экран или точка наблюдения расположены далеко от препятствия, на котором наблюдается дифракция.
Дифракция Френеля – это дифракция сходящихся лучей. Наблюдается на близком расстоянии от препятствия.
принцип Гюйгенса представляют собой правило, позволяющее, исходя из положения волнового фронта в какой-нибудь момент времени, найти положение волнового фронта для ближайшего более позднего момента времени.
Согласно принципу Гюйгенса каждую точку среды, которой достигла волна, можно рассматривать как источник вторичных сферических волн, распространяющихся со скоростью, свойственной среде. Огибающая поверхность, т. е. поверхность, касающаяся всех сферических вторичных волн в том положении, которого они достигнут к моменту времени t, и представляет собой волновой фронт в этот момент.
Поверхность, на которой расположены точки среды, выбранные в качестве источников вторичных волн, является для построения Гюйгенса вспомогательной поверхностью. Она не должна обязательно совпадать с положением какого-либо волнового фронта, но может быть поверхностью, до которой первичные волны доходят в разные моменты времени.
Для отыскания же фронта волны к моменту t надо построить положение вторичных волн к этому моменту и провести огибающую поверхность. Таким образом, из точек, достигнутых первичной волной в более ранний момент, вторичные волны успеют разойтись на большие расстояния, а из точек, позже принятых за центр вторичных волн,— на меньшие.
Принцип Гюйгенса дает возможность найти интересующую нас огибающую, выбирая вспомогательную поверхность различными способами, но окончательный результат, конечно, будет один и тот же. На рис. 272 рассматривается распространение сферической расходящейся волны, фронт которой в некоторый момент времени t0 занимает положение Р0. В разные точки вспомогательной поверхности Р свет от источника приходит в разные моменты времени. Таким образом, при применении принципа Гюйгенса можно выбирать центры вторичных волн наиболее удобным для решения данной задачи способом. Благодаря этому
Рис. 272. К пояснению принципа Гюйгенса: Р0 — вспомогательная поверхность, совпадающая в момент t0=0 с положением фронта сферической расходящейся волны; соответствующие вторичные волны (центры — светлые кружки) изображены сплошными дугами; Р — произвольная вспомогательная поверхность; соответствующие вторичные волны (центры — крестики) изображены штриховыми дугами; S — волновая поверхность в момент t, построенная как огибающая вторичных волн
Прынцып Гюйгенса — фрэнеля можна сфармуляваць наступным чынам: кожны пункт хвалевай паверхні першаснай крыницы святла можна разглядаць як крыніцу другасных хваль, «якия распаўсюджваюцца па ўсіх напрамках; гэтыя хвалі кагерэнтныя, паколькі ўсе яны ўзбуджаюцца аднымі і тымі ж першаснымі крыніцамі; светлавое поле, якое ўзнікае ў выніку інтэрферэнцыі другасных хваль, супадае з полем рэальных крыніц святла.
Такім чынам, сапраўдныя крыніцы святла можна разглядаць як паверхню, на якой безупынна размеркаваны кагерэнтныя другасныя крыніцы. У адрозненне ад рэальнай паверхні гэтая паверхня з'яўляецца абсалютна празрыстай для ўсякага выпраменьвання. Калі разглядаецца распаўсюджванне хваль, што абмежавана якой-небудзь перашкодай (напрыклад, адтулінай у непразрыстым экране), то мэтазгодна выбраць хвалевую паверхню так, каб яна датыкалася да краёў перашкоды.
Прынцып Гюйгенса — Фрэнеля можна выкарыстоўваць для атрымання закону распаўсюджвання хваль любой даўжыні.
5.
Сила света. Назовем точечным такой источник света, размерами которого можно пренебречь по сравнению с расстоянием от места наблюдения до источника. В однородной и изотропной среде волна, излучаемая точечным источником, будет сферической. Для характеристики точечных источников света применяется сила света I, которая определяется как поток излучения источника, приходящийся на единицу телесного угла: I=dФ/dΩ. (dФ — световой поток, излучаемый источником в пределах телесного угла dΩ). В общем случае сила света зависит от направления: I = I 
) 
— полярный и азимутальный углы в
сферической системе координат). Если I не зависит от направления, источник света называется зотропным. Для изотропного источника I=Ф/4π, где Ф — полный световой поток, излучаемый источником по всем направлениям. В случае протяженного источника можно говорить о силе света элемента его поверхности dS. Тогда под dФ в формуле следует понимать световой поток, излучаемый элементом поверхности dS в пределах телесного угла dQ. Единица силы света — свеча (св) является одной из основных единиц Международной системы единиц (СИ). Ее значение принимается таким, чтобы яркость полного излучателя при температуре затвердевания платины была равна 60 св на 1 см 2 (ГОСТ 9867-61).
Световой поток. Единицей светового потока является люмен (лм). Он равен световому потоку, излучаемому изотропным источником с силой света в 1 св в пределах телесного угла в один стерадиан:
1 лм = 1 св • 1 стер. Опытным путем установлено, что световому потоку в 1 лм, образованному излучением с длиной волны I = 0,555 мк, соответствует поток энергии в 0,0016 вт. Величина
А=0,0016 вт/лм носит название механического эквивалента света. Световому потоку в 1 лм, образованному излучением, для которого функция видности равна V(λ), соответствует поток энергии в А/V(λ) вт.
Освещенность. Степень освещенности некоторой поверхности падающим на нее световым потоком характеризуется величиной E=dФпад/dS, называемой освещенностью (dФПад— световой поток, падающий на элемент поверхности dS). Единицей освещенности является люкс (лк), равный освещенности, создаваемой потоком в 1 лм, равномерно распределенным по поверхности в 1 м2: 1 лк = 1 лм: 1 м2). Освещенность Е, создаваемую точечным источником, можно выразить через силу света I, расстояние r от поверхности до источника и угол α между нормалью к поверхности n и направлением на источник. На площадку dS падает поток.dФпад = IdΩ, заключенный в пределах телесного угла dΩ, опирающегося на dS. Угол dΩ равен dS cos α /r2. Следовательно, dФпад= I dS cos α /r2. Разделив этот поток на dS, получим: E=Icosα/r2
Светимость. Протяженный источник света можно охарактеризовать светимостью R различных его участков, под которой понимается световой поток, испускаемый единицей поверхности наружу по всем направлениям (в пределах значений 
от 0 до π/2; —угол, образуемый данным направлением с внешней
нормалью к поверхности): R=dФисп\dS. (dФисп—поток, испускаемый наружу по всем направлениям элементом поверхности dS источника). Светимость может возникнуть за счет отражения поверхностью падающего на нее света. Тогда под d Фисп следует понимать поток, отраженный элементом поверхности dS по,всем направлениям. Светимость измеряется в тех же единицах, что и освещенность—в люксах.
Яркость. Светимость характеризует излучение (или отражение) света данным местом поверхности по всем
направлениям. Для характеристики излучения (отражения) света в заданном направлении служит яркость 
. Направление можно задать полярным углом (отсчитываемым от внешней нормали n к излучающей пло щадке 
S) и азимутальным углом φ. Яркость определяется как отношение силы света элементарной поверхности S в данном направлении к проекции площадки S на плоскость, перпендикулярную к взятому направлению. Рассмотрим элементарный телесный угол dΩ, опирающийся на светящуюся площадку S и ориентированный в направлении (,φ). Сила света площадки ΔS в данном направлении равна I= dФ)/dΩ, где dФ — световой поток, распространяющийся в пределах угла dΩ. Проекцией ΔS на плоскость, перпендикулярную к направлению (,φ) (на рис. след этой плоскости изображен пунктиром), будет ΔS co 
. Следовательно, яркость по определению равна B=dФ/dΩΔScos 
закон обратных квадратов — это закон, утверждающий, что значение некоторой физической величины в данной точке пространства обратно пропорционально квадрату расстояния от источника поля, которое характеризует эта физическая величина.
Ф=IΩ– световой поток(лм); I=dФ/dΩ– сила света(кд); E=dФ/dS– освещенность(лк); R=dФ/dS – светимость(лк)(лм\м2); B– яркость(кд\м2)
7.
Естественный и поляризованный свет
Электромагнитные волны, как мы знаем, поперечны Вместе с тем световые волны обычно не обнаруживают асимметрии относительно направления распространения (луча). Это обусловлено тем, что в естественном свете имеются колебания, совершающиеся в самых различных направлениях, перпендикулярных к лучу(рис 105). Световая волна слагается из множества цугов волн, испускаемых отдельными атомами. Плоскость колебаний для каждого цуга ориентирована случайным образом. Поэтому в результирующей волне колебания различных направлений представлены с равной вероятностью. В естественном свете колебания различных направлений быстро и беспорядочно сменяют друг друга. Свет, в котором направления колебаний упорядочены каким-либо образом, называется поляризованным. Если колебания светового вектора происходят только в одной плоскости (рис. 106), свет называют плоско- (или прямолинейно-) поляризованным. Плоскость, в которой колеблется световой вектор (т. е. вектор напряженности электрического поля Е), мы будем называть плоскостью колебаний. По историческим причинам плоскостью поляризации была названа не плоскость, в которой колеблется вектор Е, а перпендикулярная к ней плоскость. Плоско-поляризованный свет можно получить из естественного с помощью приборов, называемых поляризаторами. Эти приборы свободно пропускают колебания, параллельные плоскости, которую мы будем называть плоскостью поляризатора, и полностью задерживают колебания, перпендикулярные к этой плоскости. Колебание амплитуды А, совершающееся в плоскости, образующей угол φ с плоскостью поляризатора, можно разложить на два колебания с амплитудами А|| = A cos φ и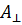 
=Asinφ(рис. 107; луч перпендикулярен к плоскости рисунка). Первое колебание пройдет через прибор, второе будет задержано. Интенсивность прошедшей волны пропорциональна A||2=A2cos2φ, Т. е. равна Icos2φ, где I— интенсивность колебания с амплитудой А. Следовательно, колебание, параллельное плоскости поляризатора, несет с собой долю интенсивности, равную cos2 ф. В естественном свете все значения φ равновероятны. Поэтому доля света, прошедшего через поляризатор, будет равна среднему значению cos2φ, т. е. 1/2- При вращении поляризатора вокруг направления естественного луча интенсивность прошедшего света остается одной и той же, изменяется лишь ориентация плоскости колебаний света, выходящего из прибора. Пусть на поляризатор падает плоско-поляризованный свет амплитуды A0 и интенсивности I0 (рис. 108). Сквозь прибор пройдет составляющая колебания с амплитудой А=A0cosφ, где φ — угол между плоскостью колебаний падающего света и плоскостью поляризатора. Следовательно, интенсивность прошедшего света I определяется выражением: I=I0cos2φ; Соотношение носит название закона Малюса. Поставим на пути естественного луча два поляризатора, плоскости которых образуют угол φ. Из первого поляризатора выйдет плоско-поляризованный свет, интенсивность которого I0 составит половину интенсивности естественного света Iест- Согласно закону Малюса из второго поляризатора выйдет свет интенсивности I0cos2φ. Таким образом, интенсивность света, прошедшего через два поляризатора, равна I=1/2(Iест*cos2φ). Максимальная интенсивность, равняя 1/2Iест получается при φ=0 (поляризаторы параллельны). При φ = π/2 интенсивность равна нулю — скрещенные поляризаторы света не пропускают. Свет, в котором колебания одного направления преобладают над колебаниями других направлений, называется частично поляризованным. Такой свет можно рассматривать как смесь естественного и плоскополяризованного. Если пропустить частично поляризованный свет через поляризатор, то при вращении прибора вокруг направления луча интенсивность прошедшего света будет изменяться в пределах от Imax до Imin, причем переход от одного из этих значений к другому будет совершаться при повороте на угол φ = π/2 (за один полный поворот два раза будет достигаться максимальное и два раза минимальное значение интенсивности). Степенью поляризации называют выражение: P=(Imax-Imin)/(Imax+Imin) Для плоско-поляризованного света Imin = 0 и Р = 1; для естественного света Imax = Imin и Р = 0. Рассмотрим две когерентные плоско-пoляризованные световые волны, плоскости колебаний которых взаимно перпендикулярны. Пусть колебания в одной волне совершаются вдоль оси х (рис. 109), во второй — вдоль оси у (оси х и у лежат в перпендикулярной к лучу плоскости). Проекции световых векторов этих волн на соответствующие оси изменяются по закону:
Величины Ех и Еу представляют собой координаты конца результирующего светового вектора Е (см. рис. 109). Из учения о механических колебаниях мы знаем, что два взаимно перпендикулярных гармонических колебания одинаковой частоты при сложении дают в общем случае движение по эллипсу (в частности может получиться движение по прямой или по окружности). Аналогично, точка с координатами, т. е. конец вектора Е, движется пo эллипсу. Следовательно, две когерентные плоскополяризованные световые волны, плоскости колебаний которых взаимно перпендикулярны, при наложении друг на друга дают волну, в которой световой вектор (вектор Е) изменяется со временем так, что конец его описывает эллипс. Такой свет называется эллиптически поляризованным. При разности фаз α, кратной π, эллипс вырождается в прямую и получается плоскополяризованный свет. При разности фаз, равной нечетному числу π/2, и равенстве амплитуд складываемых волн эллипс превращается в окружность. В этом случае получается свет, поляризованный по кругу. Заметим, что частично поляризованный и естественный свет также можно представить как наложение двухплоскополяризованных волн с взаимно перпендикулярными плоскостями колебаний. Однако эти волны не когерентны, значение а в все время меняется, вследствие чего направление результирующего вектора Е изменяется беспорядочным образом. В случае естественного света амплитуды складываемых волн должны быть одинаковыми, в случае частично поляризованного света — разными. В зависимости от направления вращения вектора Е различают правую и левую эллиптическую и круговую поляризацию. Если по отношению к направлению, противоположному направлению луча, вектор Е вращается по часовой стрелке, поляризация называется правой, в противном случае — левой. Пусть эллиптически поляризованный свет падает на поляризатор. Прибор пропускает составляющую Е|| вектора Е по 
направлению плоскости поляризатора (рис. 110). Максимальное значение этой составляющей достигается в точках 1 и 2. Следовательно, амплитуда вышедшего из прибора плоскополяризованного света равна длине отрезка 01'. Вращая поляризатор вокруг направления луча, мы будем наблюдать изменения интенсивности в пределах от Imax (получающейся при совпадении плоскости поляризатора с большой полуосью эллипса) до Imin (получающейся при совпадении плоскости поляризатора с малой полуосью эллипса). Такой же характер изменения интенсивности света при вращении поляризатора получается в случае частично поляризованного света. В случае света, поляризованного по кругу, вращение поляризатора не сопровождается (как и в случае естественного света) изменением интенсивности света, прошедшего через прибор.
8.
Вектор Умова-Пойнтинга для излучения. Плотность энергии электрического поля 
E 2 / 2, а магнитного - wm = μ H 2 / 2. Подстановка в эти выражения соотношения (1) приводит к тому, что электрическая и магнитная составляющие волны создают в одном и том же месте пространства равные значения плотности энергии: we = wm. Принимая во внимание, что значительное количество наблюдаемых в оптике эффектов связано с электрическим вектором, целесообразно представить полное значение плотности энергии электромагнитной волны как: 
E 2= EH / v; Доля энергии Δ W, переносимой волной электромагнитного излучения через площадкуΔ A, перпендикулярную направлению распространения волны за время Δ t равна произведению плотности энергии волны w на величину объема Δ V пространства, пройденного волной со скоростью v за это время: Δ W = vw (δ V),а плотность мощности P, переносимой через поперечное сечение потока энергии равняется P = Δ W / (Δ A Δ t) = EH. Или 
x E 2
Это является выражением для модуля вектора Умова-Пойнтинга: 
= 
x 
Поскольку для данной точки пространства напряжённость поля меняется по закону косинуса, а любой детектор воспринимает только усреднённое по времени значение модуля вектора, то плотность мощности, воспринимаемой приёмником будет равна полной энергии, полученной за время измерения, делённоё на время измерения, т.е.усреднённой за период колебаний мощности:
= 
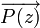vE 2(z) 
= vE 2(z) / 2
На своем опыте человечество, не сознавая этого, неоднократно встречалась с непосредственным проявлением упомянутого выше явления механического воздействия потока излучения в виде "хвостатых звёзд" - комет, шлейф которых вызван явлением "солнечного ветра"