Работа силы (сил) над системой или неточечным телом

Работа сил над системой материальных точек определяется как сумма работ этих сил над каждой точкой (работы, совершённые над каждой точкой системы, суммируются в суммарную работу этих сил над системой.

Даже если изначально тело не является системой дискретных точек, можно разбить его (мысленно) на множество бесконечно малых элементов (кусочков), каждый из которых считать материальной точкой, вычисляя работу в соответствии с определением выше. В этом случае дискретная сумма заменяется на интеграл.

§ Эти определения могут быть использованы как для какой-то конкретной силы или класса сил — для вычисления именно их работы отдельно, так и для вычисления полной работы, совершаемой всеми силами, действующими на систему.

Вопрос.

Вопрос.

17вопрос. Кинети́ческая эне́ргия — энергия механической системы, зависящая от скоростей движения её точек. Часто выделяют кинетическую энергию поступательного ивращательного движения.

Единица измерения в системе СИ — Джоуль.

Более строго, кинетическая энергия есть разность между полной энергией системы и её энергией покоя; таким образом, кинетическая энергия — часть полной энергии, обусловленная движением.

Рассмотрим систему, состоящую из одной частицы, и запишем второй закон Ньютона:

— есть результирующая всех сил, действующих на тело. Скалярно умножим уравнение на перемещение частицы . Учитывая, что , Получим:

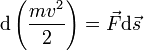
Если система замкнута, то есть , то , а величина

остаётся постоянной. Эта величина называется кинетической энергией частицы. Если система изолирована, то кинетическая энергия является интегралом движения.

Для абсолютно твёрдого тела полную кинетическую энергию можно записать в виде суммы кинетической энергии поступательного и вращательного движения:

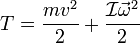
где:

— масса тела

— скорость центра масс тела

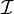— момент инерции тела

— угловая скорость тела.

18вопрос. Потенциальная энергия — скалярная физическая величина, характеризующая способность некоего тела (или материальной точки) совершать работу за счет его нахождения в поле действия сил. Другое определение: потенциальная энергия — это функция координат, являющаяся слагаемым в лагранжиане системы, и описывающая взаимодействие элементов системы^[1]. Термин «потенциальная энергия» был введен в XIX веке шотландским инженером и физиком Уильямом Ренкином.

Единицей измерения энергии в СИ является Джоуль.

Потенциальная энергия принимается равной нулю для некоторой конфигурации тел в пространстве, выбор которой определяется удобством дальнейших вычислений. Процесс выбора данной конфигурации называется нормировкой потенциальной энергии.

Корректное определение потенциальной энергии может быть дано только в поле сил, работа которых зависит только от начального и конечного положения тела, но не от траектории его перемещения. Такие силы называются консервативными.

Также потенциальная энергия является характеристикой взаимодействия нескольких тел или тела и поля.

Любая физическая система стремится к состоянию с наименьшей потенциальной энергией.

Потенциальная энергия упругой деформации характеризует взаимодействие между собой частей тела.

Потенциальная энергия в поле тяготения Земли вблизи поверхности приближённо выражается формулой:

E_p = mgh,

где E_p — потенциальная энергия тела, m — масса тела, g — ускорение свободного падения, h — высота положения центра масс тела над произвольно выбранным нулевым уровнем.

19вопрос.  В основе закона сохранения энергии лежит однородность времени, т. е. равнозначность всех моментов времени (симметрия по отношению к сдвигу начала отсчета времени). Равнозначность следует понимать в том смысле, что замена момента времени t ₁ на момент времени t ₂, без изменения значений координат и скорости частиц, не изменяет механические свойства системы. Это означает то, что после указанной замены, координаты и скорости частиц имеют в любой момент времени t ₂ + t такие же значения, какие имели до замены, в момент времени t ₁ + t.

 В основе закона сохранения импульса лежит однородность пространства, т. е. одинаковость свойств пространства во всех точках (симметрия по отношению к сдвигу начала координат). Одинаковость следует понимать в том смысле, что параллельный перенос замкнутой системы из одного места пространства в другое, без изменения взаимного расположения и скоростей частиц, не изменяет механические свойства системы.

 В основе закона сохранения момента импульса лежит изотропия пространства, т. е. одинаковость свойств пространства по всем направлениям (симметрия по отношению к повороту осей координат). Одинаковость следует понимать в том смысле, что поворот замкнутой системы, как целого, не отражается на её механических свойствах.

Между законами типа основного уравнения динамики и законами сохранения имеется принципиальная разница. Законы динамики дают нам представление о детальном ходе процесса. Так, если задана сила, действующая на материальную точку и начальные условия, то можно найти закон движения, траекторию, величину и направление скорости в любой момент времени и т. п. Законы же сохранения не дают нам прямых указаний на то, как должен идти тот или иной процесс. Они говорят лишь о том, какие процессы запрещены и потому в природе не происходят.
Таким образом, законы сохранения проявляются как принципы запрета: любое явление, при котором не выполняется хотя бы один из законов сохранения, запрещено, и в природе такие явления никогда не наблюдаются. Всякое явление, при котором не нарушается ни один из законов сохранения, в принципе может происходить.

Рассмотрим следующий пример. Может ли покоящееся тело за счет внутренней энергии начать двигаться? Этот процесс не противоречит закону сохранения энергии. Нужно лишь, чтобы возникающая кинетическая энергия точно равнялась убыли внутренней энергии.
На самом деле такой процесс никогда не происходит, ибо он противоречит закону сохранения импульса. Раз тело покоилось, то его импульс был равен нулю. А если оно станет двигаться, то его импульс сам собой увеличится, что невозможно. Поэтому внутренняя энергия тела не может превратиться в кинетическую, если тело не распадётся на части.
Если же допустить возможность распада этого тела на части, то запрет, налагаемый законом сохранения импульса, снимается. При этом возникшие осколки могут двигаться так, чтобы их центр масс оставался в покое, – а только этого и требует закон сохранения импульса.
Итак, для того чтобы внутренняя энергия покоящегося тела могла превратиться в кинетическую, это тело должно распасться на части. Если же есть еще один какой-либо закон, запрещающий распад этого тела на части, то его внутренняя энергия и масса покоя будут постоянными величинами.
Фундаментальность законов сохранения заключается в их универсальности. Они справедливы при изучении любых физических процессов (механических, тепловых, электромагнитных и др.). Они одинаково применимы в релятивистском и нерелятивистском движении, в микромире, где справедливы квантовые представления, и в макромире, с его классическими представлениями.

20вопрос. Абсолютно упругий удар — модель соударения, при которой полная кинетическая энергия системы сохраняется. В классической механике при этом пренебрегают деформациями тел. Соответственно, считается, что энергия на деформации не теряется, а взаимодействие распространяется по всему телу мгновенно. Хорошей моделью абсолютно упругого удара является столкновение бильярдных шаров или упругих мячиков.

Абсолютно упругий удар может выполняться совершенно точно при столкновениях элементарных частиц низких энергий. Это следствие принципов квантовой механики, запрещающей произвольные изменения энергии системы. Если энергии сталкивающихся частиц недостаточно для возбуждения их внутренних степеней свободы, то механическая энергия системы не меняется. Изменение механической энергии может также быть запрещено какими-то законами сохранения (момента импульса, чётности и т. п.). Надо, однако, учитывать, что при столкновении может изменяться состав системы. Простейший пример — излучение кванта света. Также может происходить распад или слияние частиц, а в определённых условиях — рождение новых частиц. В замкнутой системе при этом выполняются все законы сохранения, однако при вычислениях нужно учитывать изменение системы.

21вопрос. Абсолю́тно неупру́гий удар — удар, в результате которого компоненты скоростей тел, нормальные площадке касания, становятся равными. Если удар был центральным (скорости были перпендикулярны касательной плоскости), то тела соединяются и продолжают дальнейшее своё движение как единое тело.

Как и при любом ударе, при этом выполняются закон сохранения импульса и закон сохранения момента импульса, но не выполняется закон сохранения механической энергии. Энергия, конечно же, никуда не исчезает, а переходит в тепловую.

Хорошая модель абсолютно неупругого удара — сталкивающиеся пластилиновые шарики.

22вопрос. Гидростатическое давление — Благодаря полной малоподвижности своих частиц капельные и газообразные жидкости, находясь в покое, передают давление одинаково во все стороны; давление это действует на всякую часть плоскости, ограничивающей жидкость, с силой Р, пропорциональной величине w этой поверхности, и направленной понормали к ней. Отношение Pw, то есть давление р на поверхность равную единице, называется гидростатическим давлением. Это основное свойство жидкостей было открыто и проверено на опыте Паскалем, в 1653 г., хотя несколько ранее оно было уже известно Стивену. Простое уравнение P = pw может действительно служить для точного вычисления давления на данную поверхность сосуда, газов и капельных жидкостей, находящихся при таких условиях, что часть давления, зависящая от собственного веса жидкостей, ничтожно мала по сравнению с давлением, передаваемым им извне. Сюда относятся почти все случаи давлений газов и расчеты давлений воды в гидравлических прессах и аккумуляторах. Условно-принятые меры Г. давления всегда выражают отношения силы к поверхности, поэтому в системе абсолютных единиц (см. Единицы мер) они выражают число «дин» на кв. см, именованное число измерения:

т ¹l⁻¹ - t⁻².

В практике Гидростатическое измеряют давление в кг на 1 кв. см. Большие давления выражают часто в атмосферах, принимая за 1 атмосферу давление в 76 см столба ртути, при температуре 0° под широтой, где ускорение силы тяжести = 0,0635 кг на 1 кв. см = 6,21×10⁶ дин на 1 кв. см. 1 атмосфера = 1,0333 кг на 1 кв. см = 1,0136×10⁶ дин на 1 кв. см для широты Парижа или 1,0132×10⁶ для широты в 45°. Вычисление немного усложняется, когда надо узнать давление, производимое на не горизонтальную часть стенки сосуда вследствие тяжести налитой на него жидкости. Здесь причиной давления становится вес столбов жидкости, имеющих основанием каждую бесконечно малую частицу рассматриваемой поверхности, а высотой вертикальное расстояние каждой такой частицы от свободной поверхности жидкости. Расстояния эти будут постоянны только для горизонтальных частей стенок и для бесконечно узких горизонтальных полосок, взятых на боковых стенках; к ним одним можно прилагать непосредственно формулу Г. давления. Для боковых же стенок надо суммировать, по правилам интегрального исчисления, давления на все горизонтальные элементы их поверхности; в результате получается общее правило: давление тяжелой жидкости на всякую плоскую стенку равняется весу столба этой жидкости, имеющему основанием площадь этой стенки, а высотой вертикальное расстояние её центра тяжести от свободной поверхности жидкости. Поэтому давление на дно сосуда будет зависеть только от величины поверхности этого дна, от высоты уровня жидкости в него налитой и от её плотности, от формы же сосуда оно зависеть не будет. Это положение известно под именем «гидростатического парадокса» и было разъяснено ещё Паскалем. Действительно, оно кажется на первый взгляд неверным, потому что в сосудах с равными днами, наполненных до равной высоты одной и той же жидкостью, вес её будет очень различный, если формы различны. Но вычисление и опыт (сделанный в первый раз Паскалем) показывают, что всосуде, расширяющемся кверху, вес излишка жидкости поддерживается боковыми стенками и передается весам через их посредство, не действуя на дно, а в сосуде, суживающемся кверху, Г. давление на боковые стенки действует снизу вверх и облегчает весы ровно на столько, сколько весило бы недостающее количество жидкости. На основании сказанного выше можно Г. давление измерять также высотой столба ртути или воды, способного производить то же давление на единицу поверхности: так давление в 1 фн. на кв. дм. равно давлению столба воды в 25 дм высотой, так как фн. есть вес 25 куб. дм. воды.

23вопрос. Уравнение неразрывности струи. Рассмотрим течение идеальной жидкости внутри некоторой трубки тока, обладающей такими сечениями, что скорость молекул жидкости в любой точке каждого из них одинакова. Так как идеальная жидкость несжимаема, то ее масса, сосредоточенная между сечениями S1 и S2 трубки тока, с течением времени не изменяется. Следовательно, объемы жидкости dQ, протекшие через эти сечения за промежуток времени dt, будут равны. Поскольку dQ = S·u·dt, то выполняется соотношение:

S1·u1 = S2·u2 или
S·u = const. (14.4)

Выражение называется уравнением неразрывности. Его физический смысл заключается в том, что жидкость нигде не накапливается, т. е. за одинаковый временной интервал в трубку тока втекает и вытекает равное количество жидкости.

24вопрос. Уравнение Бернулли: