Непротиворечивость теории относительности

Теория относительности является логически непротиворечивой теорией. Это означает, что из её исходных положений нельзя логически вывести некоторое утверждение одновременно с его отрицанием. Поэтому множество так называемых парадоксов (подобных парадоксу близнецов) являются кажущимися. Они возникают в результате некорректного применения теории к тем или иным задачам, а не в силу логической противоречивости СТО.

Справедливость теории относительности, как и любой другой физической теории, в конечном счёте проверяется эмпирически. Кроме этого, логическая непротиворечивостьСТО может быть доказана аксиоматически. Например, в рамках группового подхода ^{[18] [19] [20] [21] [22]} показывается, что преобразования Лоренца могут быть получены на основе подмножества аксиом классической механики. Этот факт сводит доказательство непротиворечивости СТО к доказательству непротиворечивости классической механики. Действительно, если следствия из более широкой системы аксиом являются непротиворечивыми, то они, тем более, будут непротиворечивыми при использовании только части аксиом ^[23]. С точки зрения логики противоречия могут возникать, когда к уже существующим аксиомам добавляется новая аксиома, не согласующаяся с исходными. В аксиоматическом построении СТО, описанном выше, этого не происходит, поэтому СТО является непротиворечивой теорией^[10].

Геометрический подход

Возможны другие подходы к построению специальной теории относительности. Следуя Минковскому и более ранней работе Пуанкаре, можно постулировать существование единого метрического четырёхмерного пространства-времени с 4-координатами (ct, x, y, z). В простейшем случае плоского пространства метрика, определяющая расстояниемежду двумя бесконечно близкими точками, может быть евклидовой или псевдоевклидовой (см. ниже). Последний случай соответствует специальной теории относительности.Преобразования Лоренца при этом являются поворотами в таком пространстве, которые оставляют неизменным расстояние между двумя точками.

Возможен ещё один подход, в котором постулируется геометрическая структура пространства скоростей. Каждая точка такого пространства соответствует некоторойинерциальной системе отсчёта, а расстояние между двумя точками — модулю относительной скорости между ИСО. В силу принципа относительности все точки такого пространства должны быть равноправными, а, следовательно, пространство скоростей является однородным и изотропным. Если его свойства задаются римановой геометрией, то существует три и только три возможности: плоское пространство, пространство постоянной положительной и отрицательной кривизны. Первый случай соответствует классическому правилу сложения скоростей. Пространство постоянной отрицательной кривизны (пространство Лобачевского) соответствует релятивистскому правилу сложения скоростей и специальной теории относительности.

31вопрос. Преобразова́ния Ло́ренца — линейные (или аффинные) преобразования векторного (соответственно, аффинного) псевдоевклидова пространства, сохраняющее длины или, что эквивалентно, скалярное произведение векторов.

Преобразования Лоренца псевдоевклидова пространства сигнатуры (n-1,1) находят широкое применение в физике, в частности, в специальной теории относительности (СТО), где в качестве аффинного псевдоевклидова пространства выступает четырёхмерный пространственно-временной континуум (пространство Минковского).

Преобразование Лоренца представляет собой естественное обобщение понятия ортогонального преобразования (т.е. преобразования, сохраняющего скалярное произведение векторов) с евклидовых на псевдоевклидовы пространства. Различие между ними состоит в том, что скалярное произведение предполагается не положительно определённым, а лишь невырожденным (так называемое индефинитное скалярное произведение).

Определение

Преобразование Лоренца (лоренцево преобразование) псевдоевклидова векторного пространства 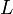— это линейное преобразование , сохраняющее индефинитное скалярное произведение векторов. Это означает, что для любых двух векторов выполняется равенство

где треугольными скобками обозначено индефинитное скалярное произведение в псевдоевклидовом пространстве .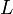

Аналогично, преобразование Лоренца (лоренцево преобразование) псевдоевклидова аффинного пространства — это аффинное преобразование, сохраняющее расстояние между точками этого пространства.

Вопрос.

33вопрос. Хотя геометрия пространства-времени не обычная (не евклидова), тем не менее эта геометрия очень похожа на евклидову, но в некоторых отношениях весьма своеобразная. Если это представление о геометрии правильно, то должны существовать такие функции координат и времени, которые не зависят от системы координат. К примеру, при обычных вращениях, если взять две точки, одну для простоты в начале координат обеих систем, а другую в любом другом месте, то в обеих системах координат расстояние между точками будет одинаково. Это первое свойство точек, которое не зависит от частного способа измерения: квадрат расстояния, или x²+y²+z², не меняется при поворотах. А как с пространством-временем? Не трудно показать, что и здесь есть нечто, не зависящее от способа измерения, а именно комбинация c²t² - x² - y² - z² одинакова до и после преобразования

 

Поэтому эта величина, подобно расстоянию, «реальна» в том смысле, который был придан этому слову выше; ее называют интервалом между двумя пространственно-временными точками, одна из которых в этом случае совпадает с началом координат. (Точнее говоря, это не интервал, а квадрат интервала, точно так же как и x²+y²+z² — квадрат расстояния.) Это название подчеркивает различие в геометриях; обратите внимание, что в формуле присутствует с, а некоторые знаки обращены.

Давайте избавимся от с, оно нам не нужно, если мы хотим иметь удобное пространство, в котором х и t можно переставлять. Представьте, к какой путанице приведет измерение ширины по углу, под которым виден предмет, а толщины — по сокращению мышц при фиксировании глаза на предмет и выражение толщины в метрах, а ширины в радианах. При преобразованиях уравнений типа (17.2) тогда получится страшная неразбериха и ни за что не удастся разглядеть всю простоту и ясность предмета по той технической причине, что одно и то же будет измеряться двумя различными единицами. С помощью уравнений (17.1) и (17.3) природа говорит нам, что время равнозначно пространству; время становится пространством; их надо измерять в одинаковых единицах. Какое расстояние измеряет секунда? Из уравнения (17.3) это легко понять: секунда — это 3*10⁸ м, расстояние, которое свет проходит за 1 сек. Иначе говоря, если бы расстояния и время мы измеряли в одинаковых единицах (секундах), то единицей длины было бы 3*10⁸ м и уравнения упростились бы. А другой способ уравнять единицы — это измерять время в метрах. Чему равен метр времени? Метр времени — это время, за какое свет проходит расстояние в 1 м, т. е. (1/3)*10⁸ сек, или 3,3 миллиардных доли секунды! Иными словами, нам нужно записать все уравнения в системе единиц, где с = 1. Когда время и пространство станут измеряться в одинаковых единицах, уравнения, естественно, упростятся:

Может быть, вы сомневаетесь в законности этого или вас «пугает», что, положив с=1, вы не сможете вернуться к правильным уравнениям? Напротив, без с их гораздо легче запомнить, а с легко поставить на нужные места, если присмотреться к размерностям. Скажем, в √(1 - u²) мы видим, что из неименованного числа 1 приходится вычитать именованное (квадрат скорости u²); естественно, этот квадрат нужно разделить на с², чтобы сделать вычитаемое безразмерным. Таким путем можно расставить с, где полагается.

Очень интересно различие между пространством-временем и обыкновенным пространством, различие между интервалом и расстоянием. Посмотрите на формулу (17.5). Если два события произошли в какой-то системе координат в одно и то же время, но в разных точках пространства, то, поместив начало координат в точку, изображающую одно из событий, мы получим, что t=0, а, например, х≠0. Значит, квадрат интервала получится отрицательным, а сам интервал — мнимым (корень квадратный из отрицательного числа). Интервалы в этой теории бывают и действительные, и мнимые, потому что их квадраты могут быть и положительными, и отрицательными (в отличие от расстояния, квадрат которого бывает только положительным). Когда интервал мнимый, говорят, что интервал между двумя событиями (точками) пространственно-подобный (а не мнимый), потому что такой интервал получался бы всегда, если бы весь мир застыл на одном времени. С другой стороны, если два предмета в данной системе координат попадают в одно и то же место в разные моменты времени, тогда t≠0, a x=y=z=0 и квадрат интервала положителен; это называется времени-подобным интервалом. Далее, если провести на диаграмме пространства-времени две прямые под углом 45° (в четырех измерениях они обратятся в «конус», называемый световым), то точки на этих прямых будут отделены от начала координат нулевым интервалом. Куда бы из начала координат ни распространялся свет, все равно x² + y² + z²=c²t², т. е. интервал между событием прихода света в любую точку и началом всегда равен нулю [как легко видеть из (17.5)]. Кстати, мы сейчас доказали, что скорость света в любых системах координат одинакова: ведь если интервал в обеих системах одинаков, то, будучи равен.нулю в одной из них, он равен нулю и в другой, и квадрат скорости света — отношение x^{`2</sup> + y<sup>`2} + z^{`2</sup> к t<sup>`2} — опять равен с².

Сказать, что скорость распространения света — инвариант,— это все равно, что сказать, что интервал равен нулю.

Вопрос.

35вопрос. Это наблюдение навело Эйнштейна на мысль, что массу тела можно выразить проще, чем по формуле (15.1), если сказать, что масса равна полному содержанию энергии в теле, деленному на с². Если (15.11) помножить на с², получается

 

Здесь левая часть дает полную энергию тела, а в последнем члене справа мы узнаем обычную кинетическую энергию. Эйнштейн осмыслил первый член справа (очень большое постоянное число m₀c²) как часть полной энергии тела, а именно как его внутреннюю энергию, или «энергию покоя».

К каким следствиям мы придем, если вслед за Эйнштейном предположим, что энергия тела всегда равна mс²? Тогда мы сможем вывести формулу (15.1) зависимости массы от скорости, ту самую, которую до сих пор мы принимали на веру. Пусть тело сперва покоится, обладая энергией m₀с². Затем мы прикладываем к телу силу, которая сдвигает его с места и поставляет ему кинетическую энергию; раз энергия примется возрастать, то начнет расти и масса (это все заложено в первоначальном предположении). Пока сила действует, энергия и масса продолжают расти. Мы уже видели (см. гл. 13), что быстрота роста энергии со временем равна произведению силы на скорость

Кроме того, F = d(mv)/dt [см. гл. 9, уравнение (9.1)]. Связав все это с определением Е и подставив в (15.13), получим

 

Мы хотим решить это уравнение относительно m. Для этого помножим обе части на 2m. Уравнение обратится в

 

Теперь нам нужно избавиться от производных, т. е. проинтегрировать обе части равенства. В величине (2m) dm/dt можно узнать производную по времени от m², а в (2mv)*d(mv)/dt — производную по времени от (mv)². Значит, (15.15) совпадает с

 

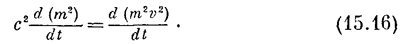
Когда производные двух величин равны, то сами величины могут отличаться не больше чем на константу С. Это позволяет написать

 

Определим теперь константу С явно. Так как уравнение (15.17) должно выполняться при любых скоростях, то можно взять v= 0 и обозначить в этом случае массу через m₀. Подстановка этих чисел в (15.17) дает

 

Это значение С теперь можно подставить в уравнение (15.17). Оно принимает вид

 

Разделим на с² и перенесем члены с m в левую часть
m²(1 - v²/c²) = m²₀,
откуда

 

А это и есть формула (15.1), т. е. как раз то, что необходимо, чтобы в уравнении (15.12) было соответствие между массой и энергией.

В обычных условиях изменения в энергии приводят к очень малым изменениям в массе: почти никогда не удается из данного количества вещества извлечь много энергии; но в атомной бомбе с энергией взрыва, эквивалентной 20 000 тонн тринитротолуола, весь пепел, осевший после взрыва, на 1 г легче первоначального количества расщепляющегося материала. Это потому, что выделилась энергия, которая имела массу 1 г, в согласии с формулой ΔЕ = Δ(mс²). Вывод об эквивалентности массы и энергии прекрасно подтвердился в опытах по аннигиляции материи — превращению вещества в энергию. Электрон с позитроном могут взаимодействовать в покое, имея каждый массу покоя m₀. При сближении они исчезают, а вместо них излучаются два γ-луча, каждый опять с энергией m₀с². Этот опыт прямо сообщает нам о величине энергии, связанной с существованием массы покоя у частицы.

Вопрос.

37вопрос. Термодинамическая система — это некая физическая система, состоящая из большого количества частиц, способная обмениваться с окружающей средой энергией и веществом. Также обычно полагается, что такая система подчиняется статистическим закономерностям. Для термодинамических систем справедливы законы термодинамики.

Описание

Для описания термодинамической системы вводят так называемые термодинамические величины — набор физических величин, значения которых определяют термодинамическое состояние системы. Примерами термодинамических величин являются:

§ температура

§ давление

§ объем

§ внутренняя энергия

§ энтропия

§ энтальпия

§ свободная энергия Гельмгольца

§ энергия Гиббса

Если термодинамическое состояние системы не меняется со временем, то говорят, что система находится в состоянии равновесия. Строго говоря, термодинамические величины, приведённые выше, могут быть определены только в состоянии термодинамического равновесия.

38вопрос. Тепловой процесс (термодинамический процесс) — изменение макроскопического состояния термодинамической системы.

Система, в которой идёт тепловой процесс, называется рабочим телом.

Тепловые процессы можно разделить на равновесные и неравновесные. Равновесным называется процесс, при котором все состояния, через которые проходит система, являются равновесными состояниями.

Тепловые процессы можно разделить на обратимые и необратимые. Обратимым называется процесс, который можно провести в противоположном направлении через все те же самые промежуточные состояния.

Можно выделить несколько простых, но широко распространённых на практике, тепловых процессов:

§ Адиабатный процесс — происходящий без теплообмена с окружающей средой;

§ Изохорный процесс — происходящий при постоянном объёме;

§ Изобарный процесс — происходящий при постоянном давлении;

§ Изотермический процесс — происходящий при постоянной температуре;

§ Изоэнтропийный процесс — происходящий при постоянной энтропии;

§ Изоэнтальпийный процесс — происходящий при постоянной энтальпии;

§ Политропный процесс — происходящий при постоянной теплоёмкости;

В технике важны круговые процессы (циклы), то есть повторяющиеся процессы, например, цикл Карно, цикл Ренкина.

Теория тепловых процессов применяется для проектирования двигателей, холодильных установок, в химической промышленности, в метеорологии.

39вопрос. Термодинамическими величинами называют физические величины, применяемые при описании состояний и процессов в термодинамических системах.

Термодинамика рассматривает эти величины как некоторые макроскопические параметры и функции, присущие системе, но не связанные с её микроскопическим устройством. Вопросы микроскопического устройства изучает статистическая физика.

Функции состояния

Функции состояния зависят только от текущего состояния системы и не зависят от пути, по которому система пришла в это состояние.

Функции состояния в термодинамике включают:

§ температуру,

§ давление,

§ объём,

§ энтропию,

а также термодинамические потенциалы.

В зависимости от выбранной модели некоторые из этих величин, строго говоря, могут быть не функциями, а независимыми переменными.

Эти величины не являются независимыми. Связь между термодинамическими параметрами для конкретной системы называется уравнением состояния.

В случае, если известно каноническое уравнение состояния, задание любой пары параметров из следующих:

§ энтропия и объём,

§ энтропия и давление,

§ температура и объём,

§ температура и давление,

позволяет вычислить остальные два параметра.

Функции процесса

Функции процесса зависят не только от текущего состояния системы, но также и от пути, по которому система пришла в данное состояние.

Функции процесса в термодинамике включают:

§ количество теплоты и

§ термодинамическую работу.

Эти величины, однако, могут быть «превращены» в функции состояния с помощью интегрирующего множителя:

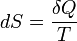§ , где S (энтропия) — функция состояния.

§ PdV = δ A, где P (давление) и V (объём) — функции состояния.

40вопрос. Идеальный газ — математическая модель газа, в которой предполагается, что потенциальной энергией взаимодействия молекул можно пренебречь по сравнению с их кинетической энергией. Между молекулами не действуют силы притяжения или отталкивания, соударения частиц между собой и со стенками сосуда абсолютно упруги, а время взаимодействия между молекулами пренебрежимо мало по сравнению со средним временем между столкновениями.

Модель широко применяется для решения задач термодинамики газов и задач аэрогазодинамики. Например, воздух при атмосферном давлении и комнатной температуре с большой точностью описывается данной моделью. В случае экстремальных температур или давленийтребуется применение более точной модели, например модели газа Ван-дер-Ваальса, в котором учитывается притяжение между молекулами.

Различают классический идеальный газ (его свойства выводятся из законов классической механики и описываются статистикой Больцмана)и квантовый идеальный газ (свойства определяются законами квантовой механики, описываются статистиками Ферми — Дирака или Бозе — Эйнштейна).