Разветвляющиеся вычислительные процессы
Логические операции и операции отношения
При описании разветвляющихся вычислительных алгоритмов кроме управляющей структуры «следование» применяется структура «развилка», или «если–то–иначе». Применяется такая структура в случае, когда нужно выбрать одну из имеющихся последовательностей действий в зависимости от выполнения или невыполнения некоторого условия. Форма записи структуры:
если <условие> то
блок1
иначе
блок2
все_если
Работа структуры организована по принципу: если <условие> истинно (выполняется), то выполняются действия1; в случае ложности (невыполнения) <условие> выполняются действия2.
Возможна вложенность структур «если–то–иначе» любой глубины, т.е. вместо действия1 и/или действия2 может быть записана еще одна структура «развилка» и т.д.
<условие> представляет собой логическое выражение. Логические выражения применяются для определения истинности или ложности определенных ситуаций. Логическое выражение – это два операнда, соединенные либо логической операцией, либо операцией отношения. Под логической операцией понимается одна из операций, связывающих два операнда: И, ИЛИ или операция отрицания НЕ, записываемая перед операндом. Если <условие> – два условия, связанные логической операцией И, то <условие> будет истинным в случае одновременного исполнения этих двух условий. Если <условие> – два условия, связанные логической операцией ИЛИ, то <условие> будет истинным в случае, когда хотя бы одно из этих двух условий будет выполняться. Результаты выполнения логических операций приведены в табл.
| Значение операнда 1 (оп1) | Значение операнда 2 (оп2) | Результат операций | ||
| НЕ(оп1) | (оп1) И (оп2) | (оп1) ИЛИ (оп2) | ||
Под операцией отношения понимается одна из операций, связывающих два операнда: > (больше), >= (больше или равно), < (меньше), <= (меньше или равно), = (==) (равно), <> (!=) (не равно). Операция отношения позволяет сравнивать числовые выражения по их значениям.
Пример. Определить условие попадания точки с координатами (x;y) в указанную область D:
Напишем условие попадания точки с координатами (x;y) в указанную область. Очевидно, что данная область должна быть разбита на две непересекающиеся области D1 и D2 (две выпуклые фигуры), т.е. D=D1UD2. Таким образом, можно установить, что точка может попасть в D1 или в D2.
Опишем условие попадания точки (х;у) в области D1 и D2:
D1: x>=-4 И x<=4 И y>=0 И y<=2
D2: x>=0 И x<=2 И y>=-2 И y<=0
Таким образом, условие принадлежности точки с координатами (x;y) области D будет следующим:
(x>=-4 И x<=4 И y>=0 И y<=2) ИЛИ (x>=0 И x<=2 И y>=-2 И y<=0)
В Excel(x – A3 y – B3):
ИЛИ(И(A3>=-4;A3<=4;B3>=0;B3<=2);И(A3>=0;A3<=2;B3>=-2;B3<=0))
Программирование разветвляющихся вычислительных процессов
Пример 1. Разработать алгоритм и составить по нему программу для вычисления значений функции y = f(x). Необходимо учитывать область определения функции:
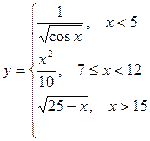
1. Построить алгоритм. В задаче требуется вычислить функцию, вид которой зависит от значения аргумента. Поэтому разобьем числовую ось значениями, указанными в формуле на несколько промежутков, указав при этом, какой должен быть результат вычислений на каждом промежутке:
При разработке алгоритма будем рассматривать промежутки числовой оси слева направо. Обозначения в алгоритме: ФНЗ – функция не задана; ФНО – функция не определена.
Записывая основной алгоритм решения задачи, вместо вычислений каждой части функции для упрощения будем писать блок1, блок2 и блок3. Поставим в соответствие каждому блоку алгоритм вычисления конкретной функции с учетом её области определения. Последний этап разработки алгоритма решения исходной задачи – подстановка в основной алгоритм вместо блоков 1,2,3 соответствующих вычислительных алгоритмов.
Сделаем небольшое замечание относительно записи текста алгоритма. Рекомендуется записывать текст алгоритма «ступеньками», т.е. новый блок «если – иначе» нужно записывать с отступом относительно предыдущего блока «если – иначе» и т.д. Так же следует поступать и при записи текста программы, соответствующей алгоритму. Одной из причин этого является то, что структура алгоритма и программы хорошо просматривается, что может помочь при обнаружении синтаксических ошибок.
Основной алгоритм:
если х<5 то
Блок1
иначе
если x<7 то
«ФНЗ»
иначе
если x<12 то
Блок2
иначе
если х<=15 то
«ФНЗ»
иначе
Блок3
все_если
все_если
все_если
все_если
Рассмотрим вычисления в каждом из блоков 1, 2 и 3 отдельно.
Блок1. Требуется вычислить функцию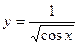 
. При вычислении учитываем, что подкоренное выражение должно быть больше или равно нулю и при этом знаменатель не должен равняться нулю. Таким образом, получаем:
если cos(х)>0 то
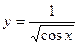
иначе
«ФНО»
все_если
Блок2. Требуется вычислить функцию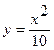 
. Здесь никаких ограничений на вычисления нет. Таким образом, получаем:
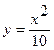
печать у
Блок3. Требуется вычислить функцию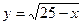 
. При вычислении учитываем, что подкоренное выражение должно быть больше или равно. Таким образом, получаем:
если 25-х >= 0 то
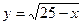
иначе
«ФНО»
все_если
В основной алгоритм вместо блоков 1,2,3 подставим алгоритмы вычисления соответствующих частей функции. В итоге получаем алгоритм решения исходной задачи.
Алгоритм
если х<5 то
если cos(х)>0 то
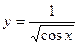
иначе
«ФНО»
все_если
иначе
если x<7 то
«ФНЗ»
иначе
если x<12 то
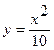
иначе
если х<=15 то
«ФНЗ»
иначе
если 25-х>=0 то
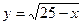
иначе
«ФНО»
все_если
все_если
все_если
все_если
все_если
Примечание. В качестве тестового примера можно ввести следующие значения: х=16 и х=30.
=ЕСЛИ(<условие>;<выр_ист_условия>;< выр_ложн_условия>)