Модели управления запасами

Существует достаточно много моделей, которые позволяют определить оптимальный уровень инвестиций в запасы и потому многие модели получили достаточное распространение на практике. Большинство моделей в базисе своем содержат нижеприведенную (или аналогичную) формулу[28]:

 

 

Рассмотрим некоторые из этих моделей.

1. Модель экономически обоснованной потребности в запасах (EOQ). Математическая модель EOQ определяет оптимальный объем запасов исходя из цели минимизации затрат на их приобретение и хранение при удовлетворении прогнозируемого спроса на эти товары. Эти затраты варьируются в зависимости от заказанного количества так, как показано на рисунке 3.

Рис.3. Варьирование затрат

Остальные характеристики модели следующие:

- Спрос на товары в единицу времени известен определенно;

- Запасы расходуются с линейным темпом.

- Затраты на осуществление закупок и загрузку материальных ценностей на склады остаются постоянными, и нет никаких скидок за покупки в больших объемах;

- Сроки реализации заказа — заранее известны и равны нулю;

- Дефициты недопустимы;

- Пополнение запасов осуществляется мгновенно.

При этих параметрах оптимальная партия заказа, основанная на критерии минимизации совокупных затрат, определяется уравнением[29]:

где:

D — годовой спрос на товар, ради которого формируются запасы (тн);

C₀ — стоимость оформления заказа (руб.); при более сложных трактовках модели сюда включается также подготовка материалов к производству, оснастка, контроль качества;

С_h — совокупные годовые затраты на хранение единицы товара за период (руб.). В эти затраты входят издержки по транспортировке и складированию, страхование, потери от хищений и порчи, альтернативные издержки от инвестиций в запасы;

Q_опт — оптимальная партия заказа (тн).

2. Модель планирования потребности в материалах (MRP) – представляет собой компьютерную информационную систему, предназначенную для обработки заказов и графика формирования запасов, зависящего от спроса на продукцию компании. MRP предназначена для ответа на три вопроса: что, сколько и когда необходимо. Основными компонентами модели являются, во-первых, накладная на предметы материально-технического обеспечения, которая определяет, что потребуется для производства конечного продукта. Накладная формируется на основе компьютерной имитации каждого продукта, которая дает описание его материальной структуры, статуса в запасах и процесса производства. Во-вторых, это основной график, который показывает, сколько компании потребуется поставить конечных продуктов и когда. В-третьих, это база данных (в бумажном варианте — картотека учета) товарно-материальных ценностей, в которой зафиксировано, какое количество запасов имеется в наличии и сколько заказано.

Вся эта информация обрабатывается с помощью различных компьютерных программ, чтобы определить потребности в материалах для каждого планового периода. В результате компьютерной обработки получается плановый график выполнения заказов, отправка заказов, необходимые коррекции в заказах, отчет об исполнении поставок, плановый отчет и отчет об отклонениях от плана выполнения заказов.

Полученный с помощью компьютерной имитации расчет потребности в комплектующих изделиях используется для определения графика загрузки оборудования в производственных цехах. Эти графики сравниваются с мощностью каждого из цехов для того, чтобы определить возможность выполнения основного графика. Если находятся узкие места, то основной график пересматривается. Когда это сделано, размещаются заказы на покупки и составляется график операций по цехам.

3. Система «точно в срок» (JIT). Каждая система стремится создать такой объем запасов, чтобы он удовлетворял прогнозируемый спрос. И в то же время она должна функционировать с наименьшими затратами. Наибольших успехов в практическом воплощении этой задачи добились японские компании, в первую очередь автомобильные, создав систему управления запасами «точно во время», которая известна как «Канбан». В системе JIT санкционирование производства детали, которая должна производиться на каждом рабочем месте, генерируется путем требования на деталь, исходящего из следующего рабочего места на производственной линии. Так как детали потребляются на конечной сборочной линии, карточки, в которых дана заявка на детали, посылаются для определения потребности и санкционирования производства замещающих деталей. Процесс повторяется на всех предшествующих рабочих местах, продвигая детали через производственную систему по мере того, как они становятся нужны, и, соответственно, определяя объемы закупок сырья и покупных деталей у поставщиков. Подобный подход получил название «вытягивание спроса». Благодаря такой системе, сокращается незавершенное производство, а также санкционируется заявка именно на те детали, которые попадают «как раз вовремя», чтобы быть использованы, что приводит к «нулевому запасу» или «производству без запасов». Комплектующие в этой системе поступают прямо в сборочный цех, минуя склад.

4. Метод ABC - классифицирует группы товаров в запасах в зависимости от их важности. Наибольшее внимание уделяется товарам группы «А», самым дорогим, меньшее товарам менее дорогим (группа «В»). Самым дешевым товарам из группы «С» уделяется наименьшее внимание.

Классификация запасов по группам товарно-материальных ценностей осуществляется с помощью пошаговой процедуры. Первый шаг состоит в том, чтобы разбить весь ежегодный объем запасов на отдельные единицы: готовые изделия по видам (например, автомобили по маркам), сырье по группам (стекла, кузова) и пр. На втором шаге путем умножения стоимости единицы на ожидаемое годовое использование рассчитывается годовое использование каждого типа запасов в денежных единицах. Третий шаг ранжирует каждую группу запасов от самой крупной по годовому использованию в денежном выражении до самой малой. Четвертый классифицирует запасы. Это делается, например, так: в группу А включают первые 20% единиц товарно-материальных ценностей, в группу В — следующие 30% и, наконец, в группу С — последние 50%. При этом в денежном выражении группа А составит, например, 70% стоимости запасов, группа В — 20%, группа С — 10%. Цифры, разумеется, могут быть и другими, это зависит от целей компании, от того, планируются ли разные типы контроля для каждой группы и какие ресурсы имеются для управления запасами.

Рис.4. Модель с фиксированным уровнем запаса

5. Модель с фиксированным уровнем запаса работает так: на складе есть максимальный желательный запас продукции, потребность в этой продукции уменьшает ее количество на складе, и как только количество достигнет порогового уровня, размещается новый заказ.

Оптимальный размер заказа выбирается таким образом, чтобы количество продукции на складе снова ровнялось максимально желательному запасу. Так как продукция не поставляется мгновенно, то необходимо учитывать ожидаемое потребление во время поставки. Поэтому необходимо учитывать резервный запас, служащий для предотвращения дефицита.

6. Модель с фиксированным интервалом времени между заказами работает следующим образом: с заданной периодичностью размещается заказ, размер которого должен пополнить уровень запаса до максимально желательного запаса.

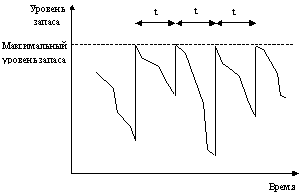
Рис.5. Модель с фиксированным интервалом времени между заказами

7. Модель с установленной периодичностью пополнения запасов до установленного уровня работает следующим образом: заказы делаются периодически (как предыдущем), но одновременно проверяется уровень запасов. Если уровень запасов достигает порогового, то делается дополнительный заказ.

8. Модель «Минимум — Максимум» работает следующим образом: контроль за уровнем запасов делается периодически, и если при проверке оказалось, что уровень запасов меньше или равен пороговому уровню, то делается заказ.

Следует отметить, что на практике применяются и другие модели управления запасами, причем выбор конкретной модели зависит от специфики бизнеса и иных влияющих факторов

3.

Модель теории очередей иначе называется моделью оптимального обслуживания, используется для определения максимального числа каналов обслуживания по отношению к потребности в них. К ситуациям, в которых модель теории очередей может быть полезна, следует отнести звонки людей в авиакомпанию для резервирования места и получения информации, ожидание очереди на машинную обработку данных, мастеров по ремонту оборудования, очередь грузовиков под разгрузку на склад, ожидание клиентами банка свободного кассира. Если клиентам слишком долго приходится ждать кассира, они могут решить перенести свои счета в другой банк. Таким образом, принципиальная проблема заключается в уравновешивании расходов на дополнительные каналы обслуживания и потерь от обслуживания ниже оптимального уровня при потере клиентов. Модель теории очередей снабжает руководство инструментом определения оптимального числа каналов обслуживания, которые необходимо иметь, чтобы сбалансировать издержки в случае малого или чрезмерно большого их количества.

 

Модели теории массового обслуживания (модель СМО с отказами). Пусть имеется n каналов обслуживания, на который поступает поток зая-вок с интенсивностью l. Поток обслуживаний имеет интенсивность m. Задача состоит в нахождении предельных вероятностей состояния систе-мы и показателей ее эффективности: А – абсолютная пропускная способность – среднее число заявок, обслу-живаемых в единицу времени. Q – относительная пропускная способность – средняя доля пришедших заявок, обслуживаемых системой. Pотк – вероятность отказа, т.е. вероятность того, что заявка покинет СМО необслуженной. Kср – среднее число занятых каналов. Предельные вероятности состояния: k=1,2,3, …, n - приведенная интенсивность потока заявок. - вероятность отказа – предельная вероятность того, что все n каналов системы будут заняты. Относительная пропускная способность – вероятность того, что заявка будет обслужена: Абсолютная пропускная способность: Среднее число занятых каналов есть математическое ожидание числа занятых каналов. Каждый занятый канал в единицу времени обслуживает в среднем m зая-вок, а с другой стороны А – интенсивность потока обслуженных системой зая-вок в единицу времени, тогда

Теория массового обслуживания (теория очередей) — раздел теории вероятностей, целью исследований которого является рациональный выбор структуры системы обслуживания и процесса обслуживания на основе изучения потоков требований на обслуживание, поступающих в систему и выходящие из неё, длительности ожидания и длины очередей ^[1]. В теории массового обслуживания используются методы теории вероятностей и математической статистики.

Однородный поток

Поток заявок однороден, если:

· все заявки равноправны,

· рассматриваются только моменты времени поступления заявок, т.е. факты заявок без уточнения деталей каждой конкретной заявки.

[править]Поток без последействия

Поток без последействия, если число событий любого интервала времени (, ) не зависит от числа событий на любом другом непересекающемся с нашим (, ) интервале времени.

Стационарный поток

Поток заявок стационарен, если вероятность появления n событий на интервале времени (, ) не зависит от времени , а зависит только от длины этого участка.

Простейший поток

Однородный стационарный поток без последействий является простейшим, потоком Пуассона.

Число событий такого потока, выпадающих на интервал , распределено по Закону Пуассона:

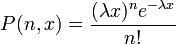
Пуассоновский поток заявок удобен при решении задач ТМО. Строго говоря простейшие потоки редки на практике, однако многие моделируемые потоки допустимо рассматривать как простейшие.

[править]Мгновенная плотность

Мгновенная плотность (интенсивность) потока равна пределу отношения среднего числа событий, приходящихся на элементарный интервал времени (, ) к длине интервала (), когда последний стремится к нулю.

или, для простейшего потока,

где равно математическому ожиданию числа событий на интервале .

[править]Формула Литтла

Среднее число заявок в системе равно произведению интенсивности входного потока на среднее время пребывания заявки в системе.

1.

Анализ математической стороны и основных принципов теории игр был дан Джоном фон Нейманом еще в 1928 году. В этой ранней работе Нейман не разбирал практические приложения задач, сосредоточив основное внимание на логических основах квантовой механики. В1944 году фон Нейман и Моргенштерн опубликовали свою хорошо известную работу "Теория игр и экономического поведения", положившую начало бурному развитию математического исследования игр. Эта работа явилась основным толчком для развития линейного программирования и теории статистических решений Вальда. Она открыла также новый подход к задачам выбора решений в конкурентных ситуациях. За последние годы появилось несколько книг по теории игр. В книге "Введение в теорию игр" Маккинси дает прекрасный математический анализ общей теории с основным упором на игры двух лиц. Он рассматривает связь теории игр с линейным программированием и теорией статистических решений.
Природа игр
В каждой игре есть цель или конечное состояние, к которому стремятся игроки, выбирая направления допустимых по правилам игры действий. В некоторых случаях смысл игры заключается в достижении цели с наибольшей эффективностью. Эффективность может измеряться счетом, как в гольфе и бейсболе.?
Игры с одним участником — игры без конкуренции. Участник играет на счет или для достижения цели.
Нас интересуют игры с конкуренцией. Конкурентная игра — это такая игра, где существует конечное состояние (вы игрыш), которого добивается каждый игрок, но не каждый может его добиться. Таким образом, по отношению к этой цели игроки находятся в противоречии. Но, благодаря правилам игры, это противоречие приводит к общему направлению действий. Каждый игрок имеет множество ходов. Выбрать один из них — значит сделать ход. Партия — это последовательность или множество ходов, которые приводят игру к конечному состоянию.
Во многих играх достижение цели ^) сопровождается каким-нибудь вы игрышем, в частности, денежным. Эти вы игрыши и про игрыши (отрицательные вы игрыши) являются в некотором смысле способом счета игры, т.е. служат выражением эффективности.
Игра с нулевой суммой — это такая игра, в которой сумма вы игрышей участников после конца игры равна нулю.
Стратегия — это установленный игроком метод выбора ходов в течение игры. Таким образом, стратегия — это совокупность правил выбора решения.
Платежная матрица — это таблица, которая определяет, какие платежи должны быть сделаны после завершения игры.
Теория игр не пытается описывать, как могла бы быть проведена игра. Она содержит процедуру и принципы, при помощи которых можно отбирать партии. В действительности теория игр является теорией принятия решений, применимой к конкурентным ситуациям.
Прямоугольные игры
Пример. Игрок А имеет три возможных плана игры (чистая стратегия): Р, О, И. Игрок В имеет два возможных плана игры: Б, Т.
Правила игры устанавливают, что в соответствии с выбранными планами приводятся следующие платежи.
Рассмотрим игрока В. Очевидно, что план Т для него невыгоден. Если он выбирает этот план, он всегда про игрывает. Таким образом, его оптимальная стратегия — всегда выбирать план Б. В худшем случае (когда А выберет план И) он про играет 1 грн.
Теперь обратимся к игроку А. Ему достанется наибольший вы игрыш, если он выберет план О, аВ выберет план Т. Но вряд ли это произойдет, т.к. из-за предыдущих рассуждений В никогда не выберет план Т. То лучшее, что может сделать А (если выберет Б),— это выбрать план И, в этом случае игрок А вы играет 1 грн.
Таким образом, мы нашли полное решение игры. Кроме того, при этом решении игрок А вы игрывает 1 грн, а игрок В про игрывает 1 грн. В этом случае 1 грн является ценой игры.
Такая игра называется прямоугольной игрой, так как ее матрица вы игрышей прямоугольная. Чтобы получить решение прямоугольной игры, необходимо найти оптимальное решение, т.е. определить:
1. Оптимальные стратегии для двух игроков.
2. Цену игры.
Принцип минимакса и максимина
Пример. Рассмотрим платежную матрицу прямоугольной игры.
Решим задачу, пользуясь рассуждениями по предыдущему примеру (рис. 6.5).
Метод 1. Игрок А никогда не выберет план Р, т.к. он всегда с большим успехом может выбирать Q или план R. Учитывая это, игрок В не может вообще принимать расчет в план Р. В этом случае, очевидно, он не выберет Т, так как для него всегда выбор S выгоднее. В свою очередь, А основывается на том, что В выберет S, и, таким образом, его лучшая политика в игре — план R. Итак, мы пришли к решению.
Оптимальная стратегия игрока А: план R.
Оптимальная стратегия игрока В: план S.
Цена игры для А: 1 грн (вы игрыш).
Цена игры для В: 1 грн (про игрыш).
Метод 2. Теперь рассмотрим следующие рассуждения.
Игрок А:
При плане Р его наименьший (min) вы игрыш — 4 грн.
При плане Q его наименьший (min) вы игрыш - 1 грн.
При плане R его наименьший (min) вы игрыш +1 грн.
Наибольший (max) из наименьших (min) возможных вы игрышей 1 грн. Значит, мы можем сказать, что "максимин для А" равен одной гривне (что соответствует выборам R, S).
Игрок В:
При плане S его наибольший (максимум) про игрыш 1 грн.
При плате Т его наибольший (максимум) про игрыш 3 грн.
Таким образом, (минимум) из наибольших про игрышей -1 грн. Мы говорим, что " минимакс для В" равен 1 грн (что опять соответствует выборам R, S).
В математических обозначениях "максимин" для А записывается выражением max(i) min(j) aij
где а, элемент 5 й строки н >го столбца платежной млгршхы.
Точно тдкжг •мпш»мякгл.тя В» обозначается выражением г
Игрок Л чожет ВМ111 РАТЬ С?. но больше чем (1 игрок В может не
В математических символах платежная матрица нашего примере представляет собой матрицу [пШ. 1 = I, й. 3: ] - 1, Й а результаты пядаются равенствами
Таким образом, решение эядпется ныбором шгяноэ К и 8 (соответствуют л* п31) игроками Л и В,
Седловые точки
Не всякая прямоугольная игра приводит к решениям с единственным оптимальным выбором для обоих игроков АиВ. Например, задана платежная матрица (рис. 6.6.)
Если А берет план Р1, то В, очевидно выберет план Б. Если А выберет план О, то В выберет план Т. Мы видим, для А нет определенного лучшего плана. То же можно сказать и об игроке В.
Используя принципы минимакса, находим:
Максимин для А = -1 грн (выбор О, Т);
Игры, для которых максимии для Д равен кннпмаксу для В,
[IИ rt hi ПЛ ЮТСЯ II грим II с сел л О ВОИ ТОЧКОЙ.
В предыдущей при море седлом» тоикп СОСТОЯЛА но иыбороа R
тр оптимальная ет-рптегил лля Л — плдн ifl,
Оптимальная стратега» для В — нлян jB,
Наиболее легкий прием отыскания седловой точки заключается в определении числа, наименьшего из всех чисел своей строки и наибольшего из числа своего столбца. Если такого числа нет, то нет и седловой точки. Стратегии игроков, соответствующие найденному числу,— оптимальные стратегии игроков, а найденное число — цена игры. Если существует два или больше таких чисел, то имеется два или более решений. Каждое решение соответствует седловой точке.

 

 

Дерево решений

Дерево решений

 

Дерево решений (древовидная диаграмма, систематическая диаграмма) – инструмент, используемый для систематического рассмотрения проблемы (темы) в виде составляющих факторов (элементов), расположенных на различных уровнях и удобного представления логических связей между этими факторами (элементами). Древовидная диаграмма строится в виде многоступенчатой древовидной структуры, составными частями которой являются различные элементы (факторы, причины) рассмотрения идеи или решения проблемы. Дерево решений рекомендуется использовать в случаях: · когда необходимо изучить все возможные элементы рассматриваемой темы (проблемы); · когда необходимо неясные пожелания потребителя в отношении разрабатываемого продукта преобразовать в установленные потребности потребителя; · когда достигнуть краткосрочных целей нужно раньше получения результатов всей работы. Методика построения: 1. Четко определите тему (проблему) для рассмотрения. Запишите ее в центре левого края чистого листа бумаги. 2. Определите основные элементы (факторы) рассматриваемой темы (проблемы). Запишите их один под другим, расположив правее от наименования темы. Проведите ответвления (линии) от наименования темы к основным элементам. Для определения основных элементов можно использовать метод «мозгового штурма» или использовать карточки с заголовками, если ранее для этой темы строилась диаграмма сродства. 3. Для каждого элемента определите составляющие их подэлементы (элементы второго порядка). Запишите элементы второго порядка один под другим, расположив их правее от перечня основных элементов. Начертите ответвления от основных элементов к составляющим их подэлементам. 4. Для каждого подэлемента определите составляющие их элементы третьего порядка. Элементы третьего порядка запишите один под другим, расположив их правее элементов второго порядка. Проведите ответвления от подэлементов к составляющим их элементам третьего порядка. 5. Деление следует продолжать до тех пор, пока не будут определены все элементы рассматриваемой темы. PыSы При работе в группе это означает – до тех пор, пока все члены группы не согласятся, что дерево решений завершено или пока не исчерпаются все идеи. PыSы На мой взгляд, дерево решений по своей сути практически тождественна диаграмме Исикавы. Отличия заключаются лишь в измененном способе их изображения и небольших отличиях по применению (а цель применения - изучение всех возможных элементов (факторов) рассматриваемой темы (проблемы), общая для обеих диаграмм). Суть построения у обеих диаграмм полностью совпадает и перевести одну диаграмму в другую не представляет никаких сложностей. Вот так, всего лишь изменив способ графического представления полученных данных, можно получить совершенно разные инструменты качества.

 

Методы экспертных оценок

Основная идея прогнозирования на основе экспертных оценок заключается в построении рациональной процеду­ры интуитивно-логического мышления человека в сочета нии с количественными методами оценки и обработки по­лучаемых результатов.

Сущность методов экспертных оценок заключается в том, что в основу прогноза закладывается мнение специа­листа или коллектива специалистов, основанное на про­фессиональном, научном и практическом опыте. Различа­ют индивидуальные и коллективные экспертные оценки.

Индивидуальные экспертные оценки основаны на ис­пользовании мнений экспертов-специалистов соответству­ющего профиля. Среди индивидуальных экспертных оце­нок наиболее широкое распространение получили методы интервью, аналитический, написания сценария.

Метод интервью предполагает беседу прогнозиста с экспертом по схеме вопрос—ответ, в процессе которой прогнозист в соответствии с заранее разработанной програм­мой ставит перед экспертом вопросы относительно перспек­тив развития прогнозируемого объекта. Успех такой оцен­ки в значительной степени зависит от способности экспер­та экспромтом давать заключение по разным вопросам.

Аналитический метод предусматривает тщательную са­мостоятельную работу эксперта над анализом тенденций, оценкой состояния и путей развития прогнозируемого объекта. Эксперт может использовать всю необходимую ему информацию об объекте прогноза. Свои выводы он оформ­ляет в виде докладной записки. Основное преимущество этого метода — возможность максимального использова­ния индивидуальных способностей эксперта. Однако он ма­ло пригоден для прогнозирования сложных систем и выра­ботки стратегии из-за ограниченности знаний одного спе­циалиста-эксперта в смежных областях знаний.

Метод написания сценария следует отнести как к ин­дивидуальным, так и к коллективным экспертным оцен­кам. Его сущность и основные характеристики будут рас­крыты ниже.

Наиболее достоверными являются коллективные эксперт­ные оценки. Методы коллективных экспертных оценок предполагают определение степени согласованности мне­ний экспертов по перспективным направлениям развития объекта прогнозирования, сформулированным отдельными специалистами. В современных условиях используется математико-статистический инструментарий для обработки результатов опроса экспертов. Например, для оценки сте­пени согласованности мнений экспертов по решению той или иной исследуемой проблемы исчисляются: дисперсия оценок, среднеквадратическое отклонение оценок и на этой основе — коэффициент вариации оценок. Чем меньше зна­чение этого коэффициента, тем выше согласованность мне­ний экспертов.

Для организации проведения экспертных оценок соз­даются рабочие группы, в функции которых входят прове­дение опроса, обработка материалов и анализ результатов коллективной экспертной оценки. Рабочая группа назна­чает экспертов, которые дают ответы на поставленные воп­росы, касающиеся перспектив развития данного объекта. Количество экспертов, привлекаемых для разработки про­гноза, может колебаться от 10 до 150 человек в зависимос­ти от сложности объекта. Определяется цель прогноза, раз­рабатываются вопросы для экспертов. При проведении оп-оса необходимо обеспечить однозначность понимания от­дельных вопросов и независимость суждений экспертов. После опроса осуществляется обработка материалов, полученных в результате коллективной экспертной оцен­ки. Окончательная оценка может определяться как сред­нее суждение или как среднее арифметическое значение оценок всех экспертов.

Также могут использоваться и другие подходы. При разработке, научно-технических дрогнозов методика статистической обработки материалов предусматривает использование совокупности оценок относительной важности, сделанных экспертами по каждому из оцениваемых направлений научных исследований. Оценки важности выража­ется в баллах и могут принимать значения от 0 до 1, от 0 о 10, от 0 до 100 и т.д.

В мировой практике широкое применение нашли та­кие методы коллективных экспертных оценок, как метод коллективной генерации идей, метод 635, метод Дельфи, метод "комиссий", метод написания сценария. Рас­смотрим сущность перечисленных методов.

Суть метода коллективной генерации идей («мозговой атаки») состоит в использовании творческого потенциала специалистов при "мозговой атаке" проблемной ситуации, реализующей вначале генерацию идей, а затем их деструктурирование (разрушение, критику) с выдвижением контр-идей и выработкой согласованной точки зрения. Этот метод был разработан американцем А. Осборном, стремив­шимся решать проблемы посредством спонтанно возника­ющих идей. Нечто подобное использовали 400 лет назад индийские мастера Хинду во время своих собраний: зап­рещались критика и дискуссии, каждый мог свободно вы­ражать свои идеи, оценка делалась позже.

Метод коллективной генерации идей предполагает ре­ализацию следующих этапов. Первый этап связан с фор­мированием группы участников мозговой атаки по ре­шению определенной проблемы. Оптимальная численность группы находится эмпирическим путем. Наиболее продук­тивными признаны группы, состоящие из 10—15 человек. На втором этапе группа анализа составляет проблемную записку, в которой формулируется проблемная ситуация и содержится описание метода и проблемной ситуации. Тре­тий этап — этап генерации идей. Каждый участник име­ет право выступать много раз. Критика предыдущих выс­туплений и скептические замечания не допускаются. Ве­дущий корректирует процесс, приветствует усовершенство­вание или комбинацию идей, оказывает поддержку, тем самым освобождая участников от скованности. Продолжи­тельность «мозговой атаки" — не менее 20 мин и не более 1 ч в зависимости от активности участников. Четвер­тый этап связан с систематизацией идей, высказанных на этапе генерации. Формируется перечень идей, выделя­ются признаки, по которым идеи могут быть объединены, идеи объединяются в группы согласно выделенным при­знакам. На пятом этапе осуществляется деструктурирование (разрушение) систематизированных идей. Каждая идея подвергается всесторонней критике со стороны группы высококвалифицированных специалистов. Группа со­стоит из 20—25 человек. На шестом этапе дается оцен­ка критических замечаний и составляется список практи­чески реализуемых идей. Этот метод позволяет качествен­но и достаточно быстро проводить оценку вариантов разви­тия объекта прогнозирования.

Метод «635» — одна из разновидностей мозговой ата­ки. Цифры б, 3, 5 обозначают шесть участников, каждый из которых должен записать три идеи в течение пяти ми­нут. Лист ходит по кругу. Таким образом, за полчаса каж­дый запишет в свой актив 18 идей, а все вместе — 108. Структура идей четко определена. Возможны модифика­ции метода. Этот метод широко используется в зарубеж­ных странах (особенно в Японии) для отбора из множества идей наиболее оригинальных и прогрессивных по реше­нию определенных проблем.

Метод Делъфи — одна из первых попыток разработать более обоснованную и строгую процедуру при эксперт­ном прогнозировании, предпринятая Т. Гордоном и О. Хелмером — сотрудниками одной из корпораций США, которые в 1964 г. опубликовали результаты обобщения и статистической обработки мнений специалистов относительно перспектив развития в ряде областей науки. Он используется при прогнозировании развития науки и техники, нвестиций и других аспектов.

Цель метода Дельфи — разработка программы после­довательных многотуровых индивидуальных опросов. Ин­дивидуальный опрос экспертов обычно проводится в форме анкет-вопросников. Затем осуществляется их статистичес­кая обработка на ЭВМ и формируется коллективное мне­ние группы, выявляются и обобщаются аргументы в поль­зу различных суждений. Обработанная на ЭВМ информа­ция сообщается экспертам, которые могут корректировать оценки, объясняя при этом причины своего несогласия с коллективным суждением. Эта процедура может повторять­ся до 3—4 раз. В результате происходит сужение диапазо­на оценок и вырабатывается согласованное суждение отно­сительно перспектив развития объекта.

Особенности метода Дельфи:

а) анонимность экспертов (участники экспертной груп­пы неизвестны друг другу, взаимодействие членов группы
при заполнении анкет полностью исключается);

б) возможность использования результатов предыдущего
тура опроса;

в) статистическая характеристика группового мнения.

Этот метод помогает предопределить развитие проблем­ных ситуаций, носящих долгосрочный характер. Наши спе­циалисты, работающие в области научно-технического прог­нозирования, также разрабатывают методы обработки эк­спертных оценок. Они носят название эвристических.

Метод комиссий — один из методов экспертных оце­нок, основанный на работе специальных комиссий. Груп­пы экспертов за "круглым столом" обсуждают ту или иную проблему с целью согласования точек зрения и выработки единого мнения. Недостаток этого метода заключается в том, что группа экспертов в своих суждениях руководству­ется в основном логикой компромисса.

Метод написания сценария основан на определении логики процесса или явления во времени при различных условиях. Он предполагает установление последовательнос­ти событий, развивающихся при переходе от существую­щей ситуации к будущему состоянию объекта. Своеобраз­ным сценарием может быть описание последовательности и условий международной интеграции хозяйства стран, включающее следующие вопросы: от каких простейших форм к более сложным должен пройти этот процесс; как он повлияет на национальное хозяйство и экономические связи стран; каковы финансовые, организационные, соци­альные, юридические проблемы, которые могут возник­нуть в ходе интернационализации хозяйства.

Прогнозный сценарий определяет стратегию развития прогнозируемого объекта. Он должен отражать генераль­ную цель развития объекта, критерии оценки верхних уров­ней дерева целей, приоритеты проблем и ресурсы для достижения основных целей. В сценарии отображаются пос­ледовательное решение задачи, возможные препятствия. При этом используются необходимые материалы по разви­тию объекта прогнозирования.

Сценарий должен быть написан так, чтобы после озна­комления с ним стала ясна генеральная цель проводимой работы в свете социально-экономических задач на прогноз­ный период. Он обычно носит многовариантный характер и освещает три линии поведения: оптимистическую — раз­витие системы в наиболее благоприятной ситуации; песси­мистическую — развитие системы в наименее благоприят­ной ситуации; рабочую — развитие системы с учетом про­тиводействия отрицательным факторам, появление кото­рых наиболее вероятно. В рамках прогнозного сценария целесообразно прорабатывать резервную стратегию на слу­чай непредвиденных ситуаций.

Сценарий в готовом виде должен быть подвергнут анализу. На основании анализа информации, признанной пригодной для предстоящего прогноза, формулируются цели, определя­ются критерии, рассматриваются альтернативные решения.

При анализе и прогнозе систем широко используются прогнозный граф и дерево целей. Графом называют фигу­